Periodic Table |
 |
 |
 |
 |
 |
 |
 |
| Functional Group Database | Chemistry & Complexity: Linear Chemistry Systems |
Chemistry & Complexity: Systems
The science of chemistry – chemistry, the whole thing – is analysed in terms of systems thinking. First, the idea of the system is introduced, along with the concepts of complexity, fractal, automata, emergence & chaos. After this, some familiar chemistry topics with simple, linear behaviours are described, before moving on to regions of chemistry space where things get more complicated... Chemistry & Complexity extends over three web pages: 1, 2, 3.
Systems Thinking & Chemistry Systems
• Systems
• Definition of Terms Using Google
• Catastrophe, Complexity, Emergence, Fractals, Automata, Butterflies
• Chemistry: A Generational Science
• Systems Chemistry
• The Chemical Reaction as a System
• Summing UpLinear Chemistry Systems
• The Ergodic Hypothesis, The Principle of Equal a priori Probability & The Correspondence Principle
• Dilute, Homogeneous, Ideal Solutions
• Equilibrium Thermodynamics
• Electron & Proton Transfer
• The Periodic Table
• Periodicity & Congeneric Series
• Material Types: Elements & Binary Compounds
• Functional Groups, Homologous Series, Chemical Automata & Gliders
• Scale Up
• Quantitative Structure Activity Relationships (QSAR)
• Molecular Biology
• Linear Chemistry: Summing UpChemical Systems Prone to Complexity
• Real Compounds, Broken Terrains
• Gases, Liquids, Solids & the Phase Interaction Matrix
• Isomers & Emergent Structure
• Mechanistic Pathways
• Non-Equilibrium Thermodynamics
• Diffusion Controlled Processes
• Experiential Design: Time, Gravity, Geometry, Temperature, Chemical Potential, Physical Separation
• Synthesis
• Chemistry & Complexity: Summing Up
|
Alan Mills 1950-2003 The three pages of the Chemistry & Complexity section are dedicated to the memory of my old friend, and friend of meta-synthesis. Alan was fascinated by emergent behaviour, and was read widely on the subject. I would have greatly valued Alan's input into this page, but unfortunately this was not to be... |
Systems Thinking
During the twentieth century it became apparent that while science is excellent at explaining and modeling linear systems, the real world is non-linear and complicated.
We can calculate with exquisite precision what will happen when a sample of gas is compressed, but we cannot predict next week's weather or oil price.
The crucial word is system, and since the 1940's many researchers have looked at systems, types of system and patterns of behaviour exhibited by systems.
A system can be:
• a sample of gas in a piston
• the gas laws
• a single cell micro-organism
• a cat
• a pride of lions
• a hive of bees
• an ecosystem
• a planet
• a solar system
• a small business
• a computer operating system
• a chemical reaction
• the set of chemical reactions
Systems are objects that exist in system space. Systems are dynamic and they evolve with time.
- The evolution may be trivial and null: the pressure of a sample of gas in a sealed container held at constant temperature does not change.
- The evolution may be predicable and linear, like the motion of the moon round the earth and planets orbiting the sun (Newtonian celestial mechanics)'
- Or the evolution may be very complicated, like the development and history of a pride of lions over a 10 year period.
Systems theory is concerned with types of system and patterns of behaviour exhibited by different types of system.
One important aim of systems research is to develop mathematical tools and computer software able to model various types of system. Largely by a process Darwinian selection in the marketplace – appropriate models and software are used and promoted, inappropriate models and software are not – it has been found that different types/classes of software are suited to different types of system:
- Computer file and software applications are handled by the local operating system: Windows, Mac, LINUX, etc.
- Business systems are generally modelled using relational database (RDMS) technology.
- Engineered items are designed and manufactured using CAD/CAM software.
Systems thinkers are particularly interested in complex systems, and an important branch of systems theory is complexity theory. It has been found that large and complicated systems exhibit emergent behaviours which, while difficult to predict beforehand may be blindingly obvious with hindsight!
- A
trivial example: Bend a rod and eventually it fails (breaks)...
- More subtly: When multi-lane highways were first designed and built it was not envisaged that at high traffic densities, vehicles would bunch together and that waves of bunching would move independently of the traffic speed. As Peter Cochrane writes:
"Anyone who drives on motorways will have experienced traffic waves created by some unseen event ahead. Probably the best place to experience this phenomena in the UK is on the M25 when, for no apparent reason, the traffic speed can oscillate between 10 and 70 mph for long periods. Sometimes the traffic comes to a complete halt and then lurches forward to 40 mph and back down to zero.
"This is the classic behaviour of a system of independent entities in a serial queue having a delay between observation and action. In this case the observation might be an accident, a breakdown, or someone driving foolishly. The delay is between our eye, brain and foot. As soon as we see something and we reach for the break pedal then very shortly afterwards so does everyone else, and so the wave starts. "
- As a recent Nature editorial asked rhetorically, In Pursuit of Systems, Nature, Vol 453, 5th May 2005, pp1:
"What is the difference between a dead cat and a live cat?
"A dead cat is a collection of its component parts.
"A live cat is the emergent behaviour of the system incorporating those parts."
Definition of Terms Using Google
"A collection of interacting parts that forms an integrated and consistent whole, isolatable from its surroundings." (Calresco)
"An equation or graph is linear if the graph of an equation is a straight line." (Shodor)
"The interaction of many parts, giving rise to difficulties in linear or reductionist analysis due to the nonlinearity of circular causation and feedback effects." (Calresco)
"The study of complex phenomena in natural systems. Basic themes include the dynamics, interactions, emergence, adaptation, learning, and evolution of a system" (Wikipedia)
"Chaos is the breakdown of predictability, or a state of disorder." (Shador)
"A distinctive area of broken terrain." (Wonka)

Image by Erik Tanghe from Pixabay
"A dynamical system that is extremely sensitive to its initial conditions."
"A system whose long term behaviour is unpredictable, tiny changes in the accuracy of the starting value rapidly diverge to anywhere in its possible state space. There can however be a finite number of available states, so statistical prediction can still be useful. " (Calresco)
"Complicated patterns that are not truly random. Chaos is a cryptic form of order, what a random-number generator produces. There is, as the phrase goes, 'a sensitive dependence on initial conditions.' Because chaos was defined in a paradoxical way ('It may look random, but it's merely chaotic'), it is a term often misused or misunderstood." (William Calvin)
"Apparent disorder; more accurately, a state of unpredictability of events. The term also applies to a specific branch of mathematics relating to non-linear systems and other infinitely complex relationships." (Tom Graves... the link has died)
"Emergence is the process of deriving some new and coherent structures, patterns and properties in a complex system. Emergent phenomena occur due to the pattern of interactions between the elements of a system over time. Emergent phenomena are often unexpected, nontrivial results of relatively simple interactions of relatively simple components. What distinguishes a complex system from a merely complicated one is that in a complex system, some behaviours and patterns emerge as a result of the patterns of relationship between the elements." (Wikipedia)
"Emergence
is the process of complex pattern formation from simpler rules. This
can be a dynamic process (occurring over time), such as the evolution
of the human brain over thousands of successive generations; or emergence
can happen over disparate size scales, such as the interactions between
a macroscopic number of neurons producing a human brain capable of thought
(even though the constituent neurons are not themselves conscious).
For a phenomenon to be termed emergent it should generally be unpredictable
from a lower level description. Usually the phenomenon does not exist
at all or only in trace amounts at the very lowest level. Thus, a straightforward
phenomenon such as the probability of finding a raisin in a slice of
cake growing with the portion-size does not generally require a theory
of emergence to explain. It may however be profitable to consider the
emergence of the texture of the cake as a relatively complex result
of the baking process and the mixture of ingredients."
(Wikipedia)
Catastrophe, Complexity, Emergence, Fractals, Automata, Butterflies & The Mandelbrot Set
In the 1960s Rene Thom's catastrophe theory described a variety of systems that had domains that were prone to suddenly flipping between states, instead of gradually moving between states in a linear manner.
In systems prone to catastrophe, the equilibrium surface is said to have a cusp:
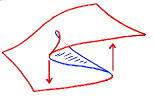
Examples of systems prone to catastrophe include:
- A rod of brittle material snapping
- A ship and its tendency to capsize
- The crystallisation of a super-cooled fluid
- The collapse of a bridge
However, it was soon realised that while illuminating, the catastrophe approach was not general and that real systems, like earthquakes, show even more complex behaviours. For example, while a single earthquake can be modelled by catastrophe theory, in reality sequences of larger earthquakes are always followed by clusters of smaller aftershocks.
Click here for the near real-time IRIS seismic monitor, one of the most impressive scientific sites on the web.
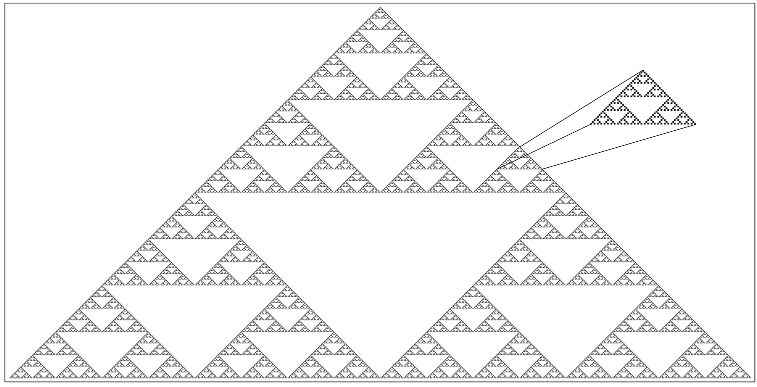
In the 1970s, Benoit Mandelbrot, at the time an IBM research mathematician, explored the looping of very simple equations. In this new mathematical space – for practical purposes only available with the advent of programmable computers – Mandelbrot discovered the extraordinary pattern that bears his name. The Mandelbrot set has been described as the most complex object in mathematics.
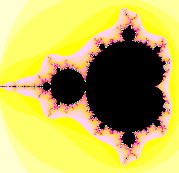
The two books by Mandelbrot: Les objets fractals. Forme, hasard, dimension (1989 ed3) and The fractal geometry of nature (1982) introduced the idea of the "fractal" and "fractal geometry" to more general audiences.
The perfect example of fractal behaviour is the Mandelbrot set itself. It is possible to infinitely zoom into the fractal edge of the Mandelbrot set and there find an infinite number of mini-Mandelbrot sets hiding in the infinite detail:
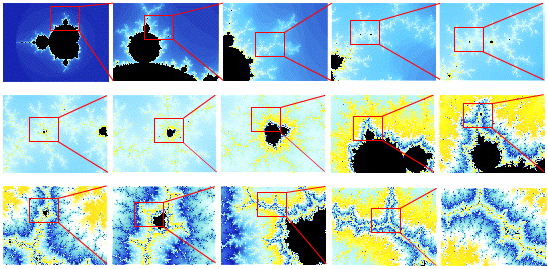
A sequence of 15 zooms into the edge of the Mandelbrot set, see here.
The excellent PC
program Fractint allows very deep zooming into the Mandelbrot set by bypassing
a computer's 16/32/64 bit maths routines, both OS & CPU. The image
of the mini-Mandelbrot set shown below is obtained at a magnification of 4 x 10^58:

4 x 1058 is a simply HUGE magnification. It is a zoom of:
x 4,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
This YouTube clip gives a deep zoom and is called: "A Mandelbrot the size of the known universe".
And an even deeper zoom: Mandelbrot Fractal Set Trip To e214 HD from teamfresh on Vimeo.
The very highly recommended Powers of 10 web site zooms from the edge of the known universe to deep inside of a proton, and that is only a magnification factor of 1039. A Homer Simpson spoof version can be found here.
Mandelbrot showed that fractals are patterns have the property of being self-similar with respect to scale, and so when looking at a fractal pattern it is not possible to deduce the scale of the image because self-similarity can occur over many orders of magnitude. Furthermore, Mandelbrot pointed out that many features of the natural world are fractal and self-similar. The famously rugged coastline of Great Britain is fractal over the scale from metres to hundreds of kilometres:
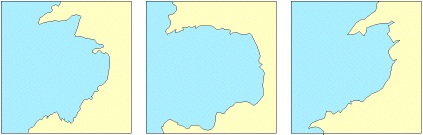
Three outline maps show parts of the Great Britain coastline, specifically parts of Wales. The map on the left shows about 1 mile, the middle map about 10 miles and the right map about 100 miles:
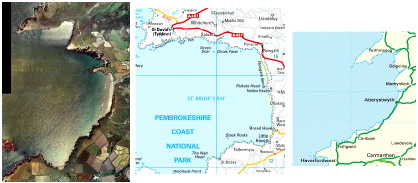
One implication of fractal and self-similar geometry is that is is not possible to come up with an accurate measure of the length of the coastline of Great Britain because the answer will be dependent upon the scale at which the measurement is taken. Thus, fractal geometries can lead to real problems for classical sciences which like to be able to provide precise numerical answers to clear questions like: "How long is the coastline of Britain?".
The coastline diagrams bring out an important feature of fractal geometry. Even though we may not know the scale, coastlines are still clearly coastlines and we do not confuse coastlines with other natural fractal system such as branching trees, mountain ranges or clouds. Our brains are excellent at distinguishing between different types of natural fractal pattern, which is useful because the natural world is so intrinsically fractal:

Psychologists and neuroscientists do not yet understand how the brain is so good at distinguishing between different types of natural fractal.
Mandelbrot showed that simple, looping non-linear equations can exhibit regular behaviour, or they can act in complex, unpredictable, chaotic ways.
Consider the looping equation (A * B * B) – 1 = B
Meaning that the numerical result of (A * B * B) – 1 is used as the value of B on the next iteration of the loop.
With certain values of A and B (0.400 and 0.630) the series decays to zero, with some it regularly oscillates between values, and with others it behaves chaotically producing "random" numbers:
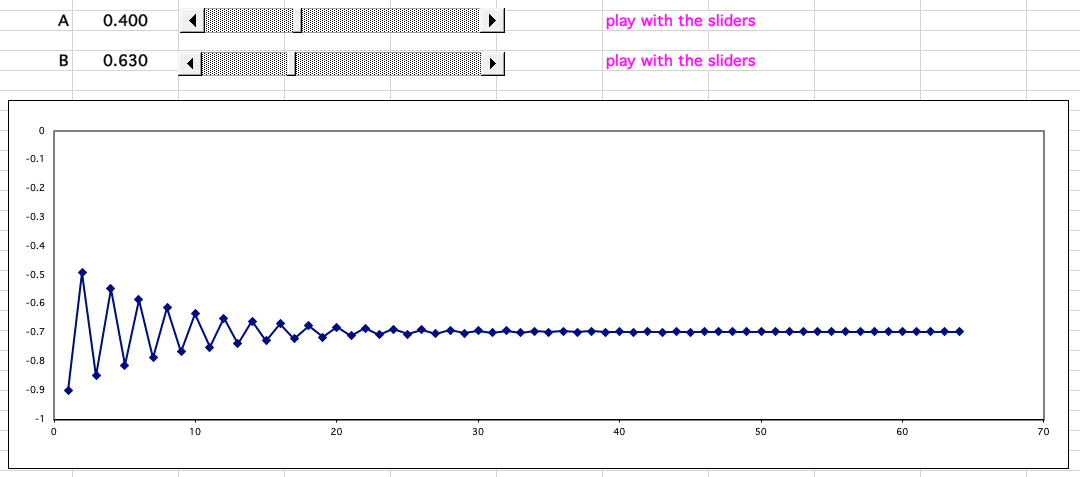

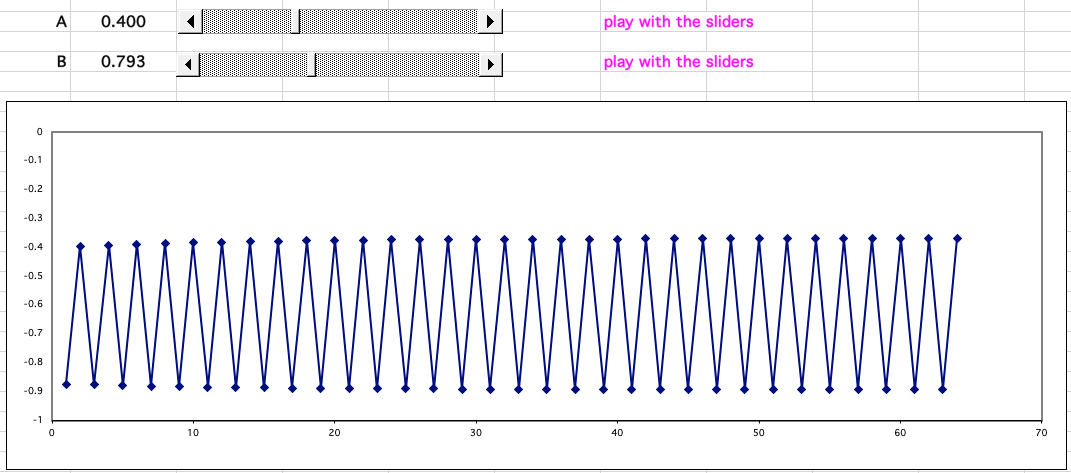
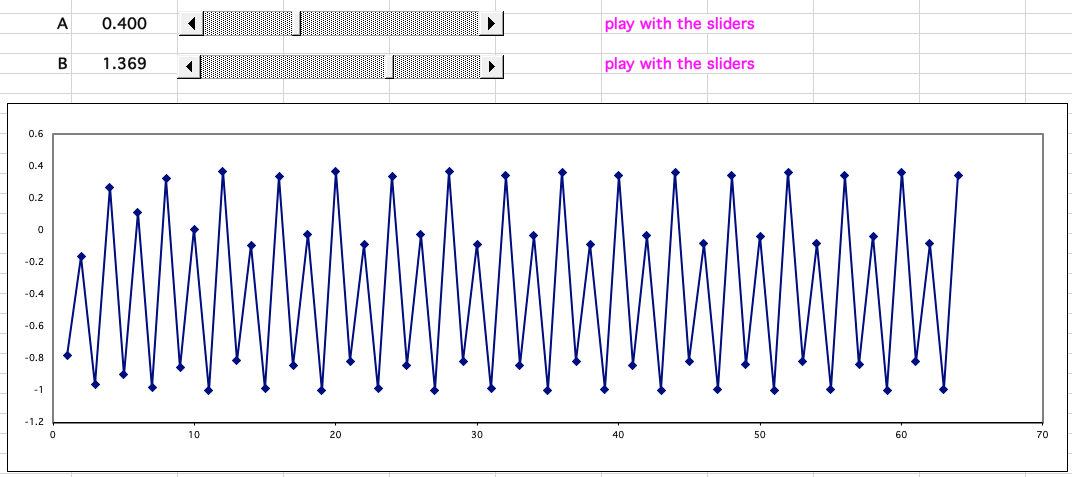
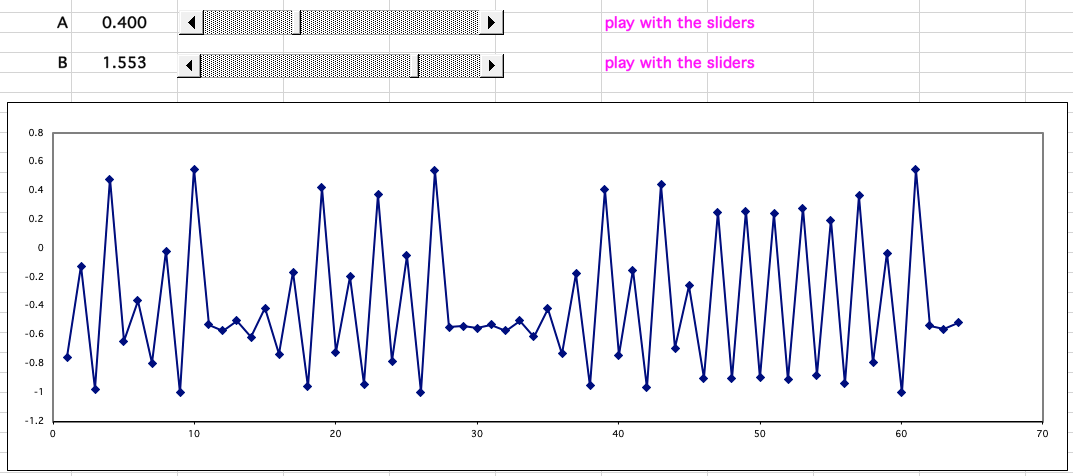
This spreadsheet model shows the famous Butterfly effect in operation: A butterfly flaps its wings in China and a hurricane forms in the Caribbean.
When the system is behaving chaotically, tiny [butterfly wing flap] changes to the constant B, for example 1.553, 1.554 and 1.555, cause wide variation so that it is not possible to predict the values of B after 20 or more iterations:

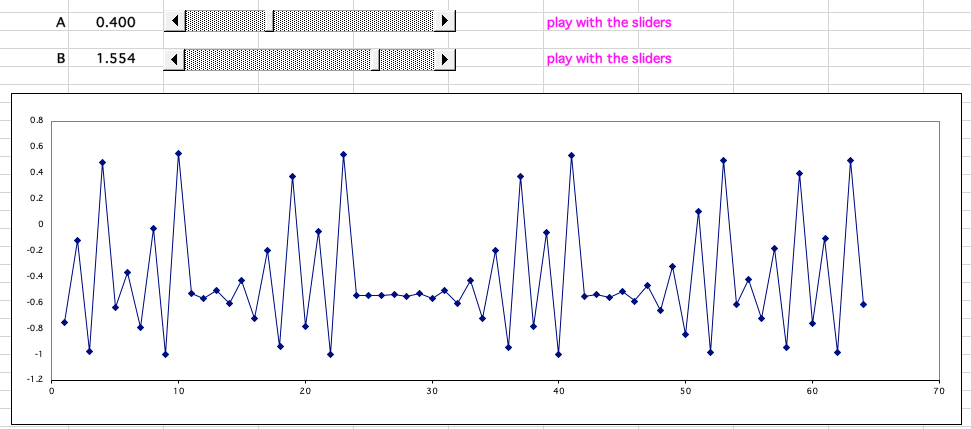
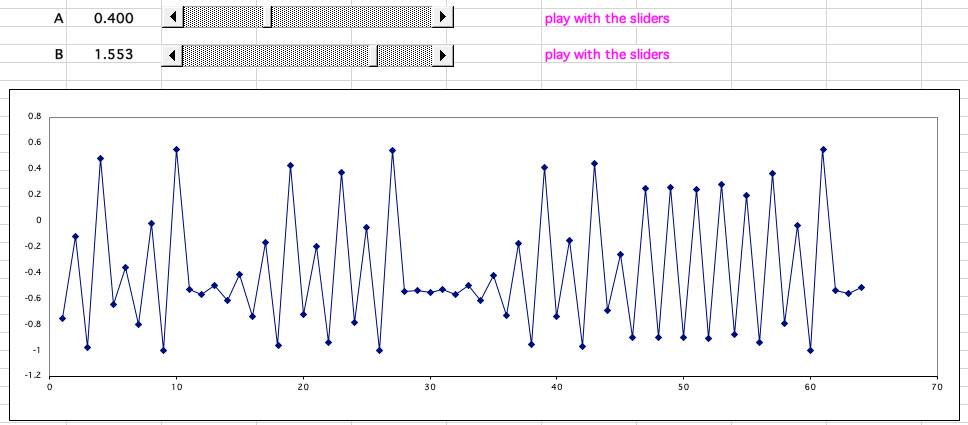
Download the Excel spreadsheet and play with the sliders, here.
Cellular automata are discrete dynamical systems whose behaviour is generative and completely specified in terms of local rules. Complex emergent behaviours can develop in even very simple systems. One of the best known and studied examples is The Game of Life invented by the British mathematician John Conway in the nineteen sixties.
The Game of Life consists of a two dimensional array of squares on a computer screen and the "game" is played over a series of steps [or generations] with two simple rules:
- If a square is off, it turns on if exactly three of its neighbours are on.
- If a square is on, it stays on if exactly two or three neighbours are on, otherwise it turns off.

From http://mathworld.wolfram.com/Life.html:
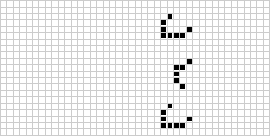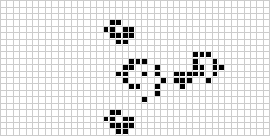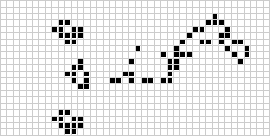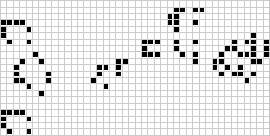
Game of Life "runs" develop in involved ways, but the individual objects always have a few common types of ending:
- On screen object may grow for a few generations until it becomes static and unchanging.
- An object may flip or cycle between two or more forms and become a "blinker" [a Game of Life term].
- An object may grow for a few generations and then shrink, self-destruct and vanish.
- An on screen object may eject a "glider" [a Game of Life term], an object which moves away from the place where it formed until it collides with the edge of the playing area.
- An interactive (java) Game of Life website can be found here. Click and have fun.
- Go to this mathworld link for an excellent discussion and history of Conway's work.
The science of cellular automata has been rigorously explored by Stephen Wolfram in his recent book, A New Kind of Science, and website, NKS and here,
Read a fair – but critical – review of this new analysis, here.
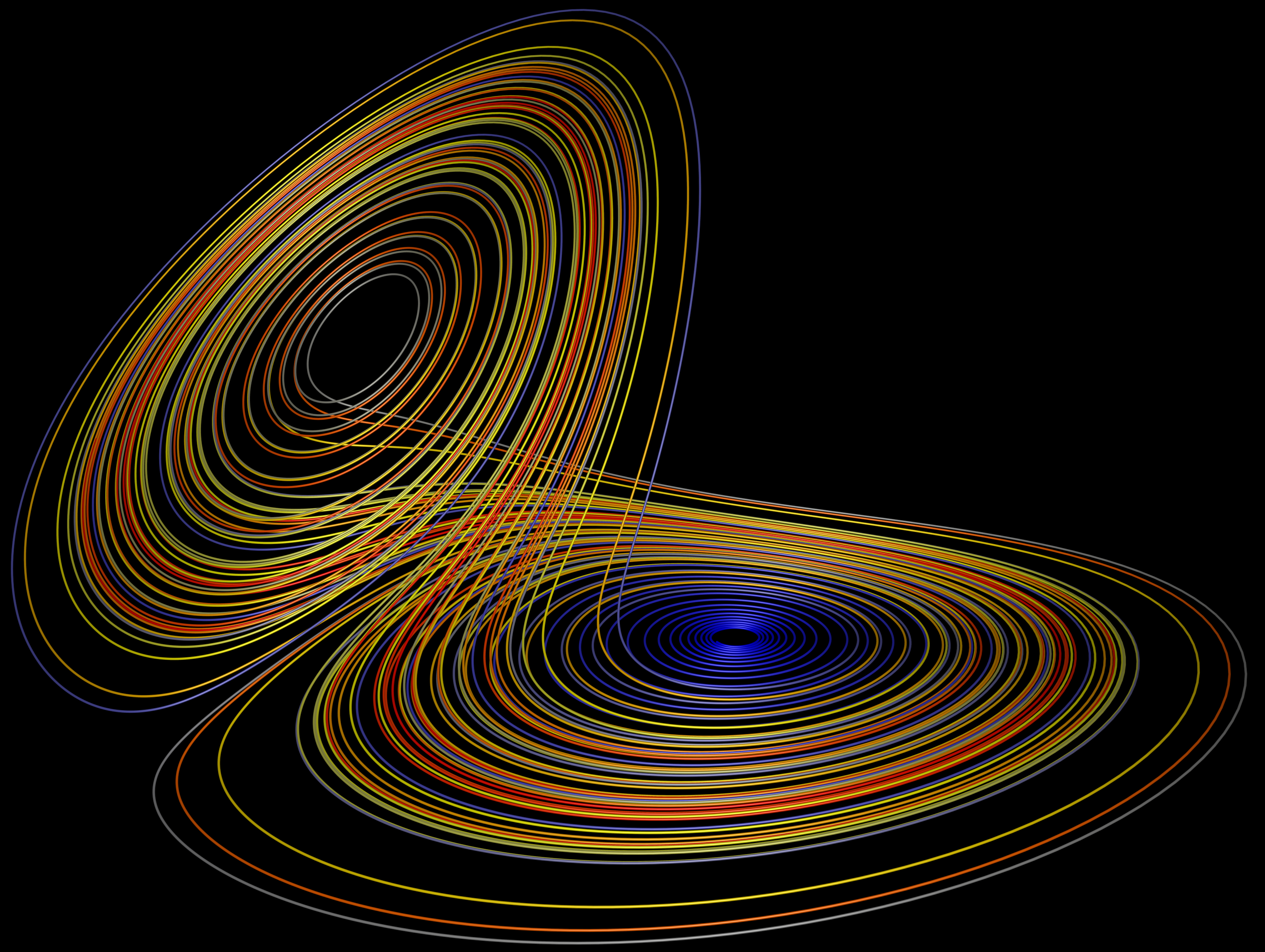
Lorenz strange attractors are useful when modeling the weather, here:
Fractal dimensions (and here), give a new way of understanding patterns:
- Line has a dimension of 1
- Plane has a dimension of 2
- Cube has a dimension of 3
- Fractal images have a dimension of between 1 and 2
- Fractal objects have dimensions between 2 and 3
Mitchell Feigenbaum, in the 1970s and like Mandelbrot also using computers to study looping mathematical functions, found a universal constant for functions approaching chaos via period doubling.
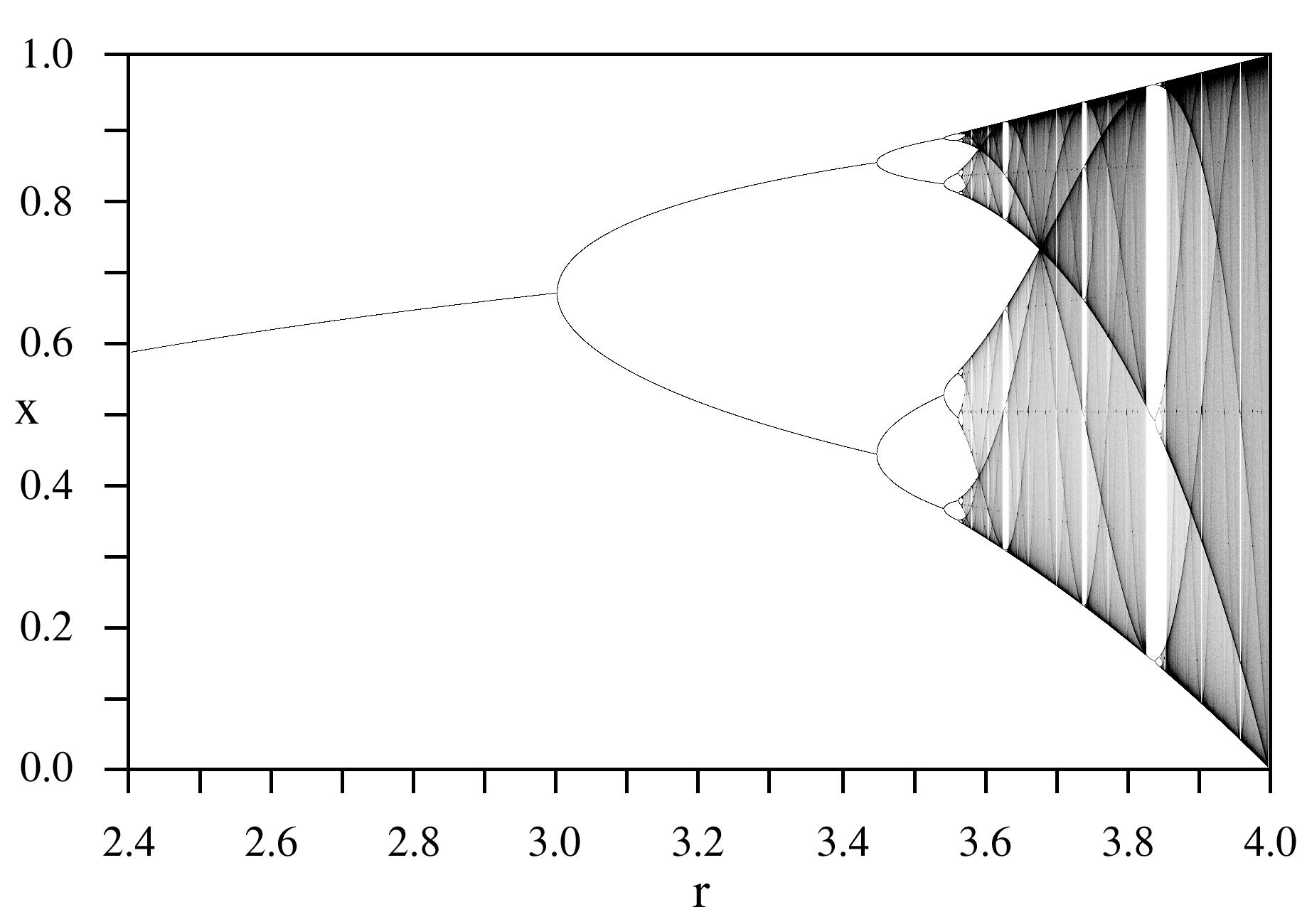
It turns out that
the Feigenbaum and Mandelbrot approaches are closely related.
Systems that Crackle
Crackling noise is associated with: earthquakes and the general fracture of disordered materials, crumpling paper, magnetizing of iron, shearing bubbles in a foam, biological extinctions, fluids invading a porous medium, fluctuations in stock markets, solar flares, sound emitted during martensitic phase transitions, and even group decision making
Complex systems are discussed in a Nature Insight collection of review articles: Nature, 410, 241-284 (2001), specially the first paper: Crackling Noise by J.P. Sethna, K.A. Dahmen & C.R. Myers pp242-250.
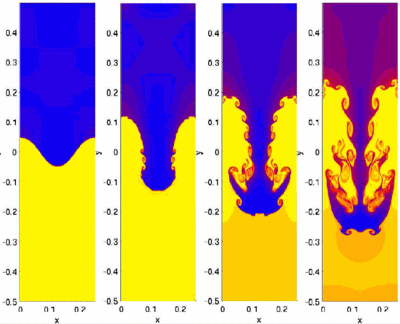
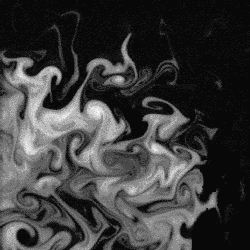
Understanding the nature of turbulence has long been recognised as a scientific and engineering problem. It is now recognised that turbulence is fractal:
In 1988 James Gleick, a science journalist, reviewed the new and emerging field in his well timed and readable book Chaos: Making a New Science. In a non-technical way, Gleick's book reviews and links together the people who made the discoveries with the various parts of [what is now known as] complexity theory.
Ian Stewart, a mathematician and communicator has written extensively on the these matters with more depth and with greater mathematical rigour.
View some extraordinary images of computer generated mathematically complex objects on the Mathematica gallery (below are some captured thumbnails):

And, there is a heap of good stuff to be found on the web. Explore some of the links from this page, or explore this excellent page of chaos & fractal links, here, or have a look at images generated by the commercial package, Untrafractal.
Systems Chemistry
"Systems chemistry deals with the emergent properties of interacting chemical systems or networks. In other words, properties that result from the interaction between the components in a network, rather than any one species acting individually." RSC
One powerful systems way to look at chemistry – as in "chemistry, the whole thing" – is to consider chemistry to be a generational science because all entities of chemical interest, with the notable exceptions of the electron and the photon, are compound objects constructed from simpler unit entities:
- Up & down quarks combine to give protons & neutrons
- Protons and neutrons combine to give atomic nuclei
- Atomic nuclei and electrons combine to give atoms and ions
- Atoms with the same proton number can be collected as bulk elements
- Elements combine to give diatomic molecules and binary compounds
- Binary compounds may be gases, liquids or solids; metallic, ionic, molecular or network materials
- Simple chemical species react with each other to give larger and ever more complex molecules
- C, H, N, O, P & S combine to give, amongst other entities, the nucleic and amino acids
- The nucleic and amino acids combine to give DNA, RNA, thousands of peptides, proteins... and life
As the entities become more complicated, emergent properties appear, as will be discussed below.
Chemistry is not unique in being generational, consider language & literature:
- Letters arrange into words
- Words arrange into phrases
- Phrases arrange into sentences
- Sentences arrange into paragraphs, sections, chapters & books
- Books are arranged in a library
- Literature mirrors and influences society
Emergent properties appear: We would not predict from the arrangement of letters in words (spelling), the rules for constructing sentences or for writing successful novels.
And motorcars:
- Individual components are arranged into the engine, chassis, bodywork sub-assemblies
- Sub-assemblies are combined into the working car
- Cars are driven
on roads with other cars obeying the rules of the road
Emergent properties appear: We would not predict from the arrangement of the nuts and bolts that, that at high traffic densities on fast moving freeways traffic bunching would occur.
As a generational science, chemistry can – in large part – be regarded as a cone of increasing complexity emanating from the periodic table of the elements:
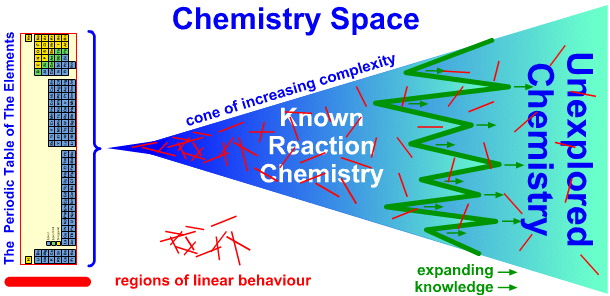
The periodic table is a schema that rationally displays the building blocks from which our physical world is constructed, the chemical elements. The cone of increasing complexity gives rise to:
- Molecules & materials
- Gases, liquids, solids
- Pure substances & mixtures of substances
- Chemical interactions & reactions between substances
- Inorganic and organic materials
- Rock, geology, biology
As a generational science consisting of many interacting particles, chemistry behaves like a cellular automata.
As Stephen Wolfram and John Conway show with with their very simple math cellular automata (discussed above), cellular automata systems can develop in simple ways or they can exhibit extremely complex behaviours. And so it is with "chemical automata"that involve real interacting chemical species: atoms, ions, molecules...
- There are regions
in chemistry space where behaviour is linear and simple, including the
gas laws, ideal dilute solutions, periodicity, etc., as will be discussed
below.
- And there are regions where the behaviour is formally complex, like the Belousov-Zhabotinsky (BZ) reaction, turbulence, mechanistic pathways, synthesis, etc.
Theory and experience tell us that as systems "enlarge", behaviour becomes more complex and new, emergent, complex properties appear, and chemistry is no different.
Note that here the term "enlarge" refers to variety of amongst the types of chemical species and variety in the rules of chemical interaction, rather than the total number of species.
The behaviours of chemical species interactions are more involved that those of the cells in Conway-Wolfram cellular automata.
Systems exhibiting linear behaviour can be found in chemistry space... amongst the complexity!
Chemical Systems
Chemistry consists of multiple systems which together explore and define chemistry space.
Consider the term "explore":
- We learn about our house, garden and the roads around it.
- Millions of ants explore every nook and cranny of their local environments.
- Googlebots and other crawlers and spiders explore web-space.
- Chemical species explore their local spaces by occupying the available quantum states:
Chemical species are quantum objects that vibrate, rotate, translate (move), and at higher energies undergo electronic transitions. The science is well understood and an array of mathematical tools – based on quantum mechanics and kinetic theory (statistical thermodynamics) – is available. The techniques involved are covered by university level physical chemistry courses and by textbooks such as Atkins' Physical Chemistry.
Chemical species explore their local chemical interaction & reaction environments. This science is the primary concern of the chemogenesis web book which takes the simplest chemical species, the main group elemental hydrides, and employs a combinatorial approach to explore the emerging reaction chemistry.
Chemical species distribute themselves between – and thereby completely explore – the local states according to temperature. This argument is sometimes expressed as the totalitarian rule (after TH White, Once and Future King):
"Everything not forbidden is compulsory."
Or in a chemical context: "Any reaction that can occur, will occur."
The equilibrium distribution of species in a system with two states, i & j, and where i is higher in energy than j, is modelled by the Boltzmann relationship:
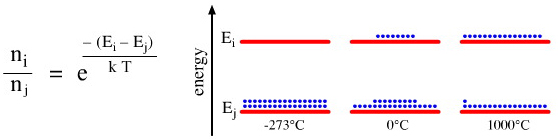
where:
n is the number of particles (mole fraction) in the states ni and nj
E is the energy of the states Ei and Ej
k is Boltzmann's constant, 1.38066 x 1023
T the thermodynamic (Kelvin) temperatureThe Boltzmann relationship tells us that at equilibrium and at absolute zero (0.00 Kelvin or –273.15°C), all species will be in the lowest energy state, Ej, and that at higher temperatures [and at thermal equilibrium, see below] there will always be more species in the lower energy state than the higher energy state.
Consider the statement: "chemistry consists of multiple systems":
Each of the following is "a system":
- An atom
- The periodic table
- A closed thermodynamic system
- Kinetic theory
- The gas laws
- A closed, half-filled jar of water
- Butane and its conformers
- A Bunsen burner flame
- A gas chromatograph
- The manufacture of methyl tertiary butyl ether, MTBE
- Inorganic chemistry
- Mechanistic theory
- The Chemical Thesaurus Reaction Chemistry Database
- The chemical literature
- Etc., etc., etc...
Chemical systems explore their local environments and in total, define the expanding boundary of chemistry space.
At school and university, chemistry is always taught on a topic-by-topic (system-by-system) basis.
The Chemical Reaction as a System
Chemistry is often described as "the study of matter and its changes".
Matter is the stuff from which our world is constructed, however, chemical scientists make the great simplification of – wherever possible – working with simple matter: pure substances, homogeneous solutions and reagent grade chemicals. Matter and its classification are discussed elsewhere in this web book, here.
The change that occurs when a sample of matter is processed: heated, compressed or mixed with another type of matter can be be described in terms of a chemical equation, a powerful metaphor because the entities may be of many types.
For example, a reaction equation employ imaginary, generic species that have arbitrary symbols like X, Y & Z.
The generic reaction equation:
X + Y → Z
can be used to model many reaction processes, see here.
Or, the entities that make up the equation may represent real chemical substances like hydrogen , oxygen and water:
2H2 + O2 → 2H2O
When all the reacting entities in a chemical equation are real reagent grade chemicals of known purity, the reaction equation can be balanced in terms of mass, charge, free energy, enthalpy and energy, below.
The reaction equation arrow: →
- Is the central & pivotal part of a chemical reaction equation.
- Is equivalent to – but is not the same as – the equality or "equals sign" in maths =
- Reactions are always
written and balanced with respect to the reaction arrow.
- Thermochemical
data is always given with respect to the reaction as written,
ie. with respect to the arrow. This convention removes any apparent
ambiguity where the enthalpy of a reaction may be expressed "per
mol", but it is not be clear what the mole is. The decomposition
of ozone would be an example: 2O3
 3O2.
3O2.
- There are several types of reaction arrow:

As written, a balanced chemical reaction equation is a closed system that evolves with time, and when we discuss a gas phase reaction involving real chemical reagents, such as:
2H2(g) + O2(g) → 2H2O(g)
the chemical reaction is the system universe:
- No edges are described
or defined in the reaction equation. These are constraints for us to
add.
- We are reduced
to inert observers inside a reaction vessel of infinite size containing
only hydrogen and oxygen and/or water.
- If the reaction involves a physical phase change, for example the conversion of water to vapour reaction system:
H2O(l) → H2O(g)
the phase surface is an infinite surface, like the boundary between an infinite ocean and an infinite atmosphere.
- The reaction equation is scale invariant: it can represent individual atoms or it can represent billions of tons of bulk material.
It was stated above that chemistry is a generational science. Each and all of these generational steps: quarks to protons & neutrons; protons + neutrons to atomic nuclei; atomic nuclei + electrons to atoms and ions; etc., can be described in terms of balanced chemical equations.
Chemical reactions and the associated symbolic reaction equations are the "unit systems" from which chemistry is constructed. The set of chemical reactions represents reaction space.
Summing Up
There are a number of theories:
Systems theory
Catastrophe theory
Chaos theory
Complexity theory
Briefly, when academics first started looking systems they realised that systems could be linear (simple) or non-linear and complicated.
Catastrophe theory was one of the first approaches to dealing with difficult non-linear systems, but the theory proved to be lacking in generality.
In the 1970s it was discovered that looping computer code could generate patterns of infinite complexity, and the term chaos was adopted to describe the extraordinary fractal patterns produced.
Mandelbrot realised that the new fractal patterns seemed to mimic the natural world, and could exhibit rare beauty. By the mid 1980s the term chaos theory entered popular culture.
It is now recognised that the terms "complex" and "complexity" are actually more useful – and carry less cultural baggage – than the term "chaos", even though the terms are sometimes [confusing] used interchangeably.
Due to complexity theory, the word "random" has rather lost its meaning because it is just a description, whereas the term complexity implies that a non-linear process is operating. Physical and natural systems that exhibit random behaviour are always complex.
Before Mandelbrot's work, the coastline of Great Britain may have been described as "a random collection of headlands and bays". Post–Mandelbrot, coastlines are recognised as being complex, fractal and self-similar.
Chemistry can be studied using systems analysis, as discussed on these pages and by a Royal Society of Chemistry Instant insight: Systems chemistry by R. Frederick Ludlow & Sijbren Otto.
 |
 |
 |
| Functional Group Database | Chemistry & Complexity: Linear Chemistry Systems |
© Mark R. Leach 1999 –
Queries, Suggestions, Bugs, Errors, Typos...
If you have any:
Queries
Comments
Suggestions
Suggestions for links
Bug, typo or grammatical error reports about this page,please contact Mark R. Leach, the author, using mark@meta-synthesis.com
This free, open access web book is an ongoing project and your input is appreciated.