Periodic Table |
 |
 |
 |
 |
 |
 |
 |
| Lewis & Brønsted Theories of Acidity | Main Group Elemental Hydrides |
Pearson's
Hard Soft [Lewis] Acid Base Principle:
The HSAB Principle
Ralph Pearson introduced his Hard Soft [Lewis] Acid Base (HSAB) principle in the early nineteen sixties, and in doing so attempted to unify inorganic and organic reaction chemistry. The impact of the new idea was immediate, however, over the years the HSAB principle has rather fallen by the wayside while other approaches developed at the same time, such as frontier molecular orbital (FMO) theory and molecular mechanics, have flourished.
This page discusses the profound limitations of the Pearson approach and compares & contrasts the HSAB principle to the chemogenesis analysis as presented in this web book.
Note, in this web book:
| Lewis acids are RED | Lewis bases are BLUE |
Irving-Williams Stability Series
The Irving-Williams stability series (1953) pointed out that for a given ligand the stability of dipositive metal ion complexes increase:
Ba2+ < Sr2+ < Ca2+ < Mg2+ < Mn2+ < Fe2+ < Co2+ < Ni2+ < Cu2+ < Zn2+
It was also known that certain ligands formed their most stable complexes with metal ions like Al3+, Ti4+ & Co3+ while others formed stable complexes with Ag+, Hg2+ & Pt2+
Ahrland's Type A, Type B Analysis
In 1958 Ahrland et al. classified metal cations as Type A and Type B, where:
Type A metal cations include:
- Alkali metal cations: Li+ to Cs+
- Alkaline earth metal cations: Be2+ to Ba2+
- Lighter transition metal cations in higher oxidation states: Ti4+, Cr3+, Fe3+, Co3+
- The proton, H+
Type B metal cations include:
- Heavier transition metal cations in lower oxidation states: Cu+, Ag+, Cd2+, Hg+, Ni2+, Pd2+, Pt2+
Ligands, chemical entities that complex with metal cations, were classified as Type A or Type B depending upon whether they formed more stable complexes with Type A metal cations or Type B metal cations, from here:
Ligand's tendency to complex with Type A Metals |
Ligand's tendency to complex with Type B Metals |
N >> P > As > Sb > Bi O >> S > Se > Te F >> Cl > Br > I |
N << P > As > Sb > Bi O << S ~ Se ~ Te F < Cl < Br << I |
From this analysis, an empirical rule can be derived:
Type A Metals prefer to bind (complex) to Type A Ligands
and
Type B Metals prefer to bind (complex) to Type B Ligands
These empirical – experimentally derived – rules tell us that Type A Metals are more likely to form oxides, carbonates, nitrides and fluorides, while Type B Metals are more likely to form phosphides, sulfides and selinides.
Railsback's Geochemical Analysis
The "Type A, Type B" analysis is of great economic importance because:
- Some metals are found in nature as Type A metal + Type A ligand minerals, such as carbonates: MgCO3 and CaCO3 and oxides: Fe2O3 and TiO2
- While others are found as Type B metal + Type B ligand minerals, for example the sulfide ores: PbS, CdS, NiS, etc.
This approach has been very successful developed in by Bruce Railsback with his excellent and highly recommended "Earth Scientist's Periodic Table website".
Click image to enlarge:
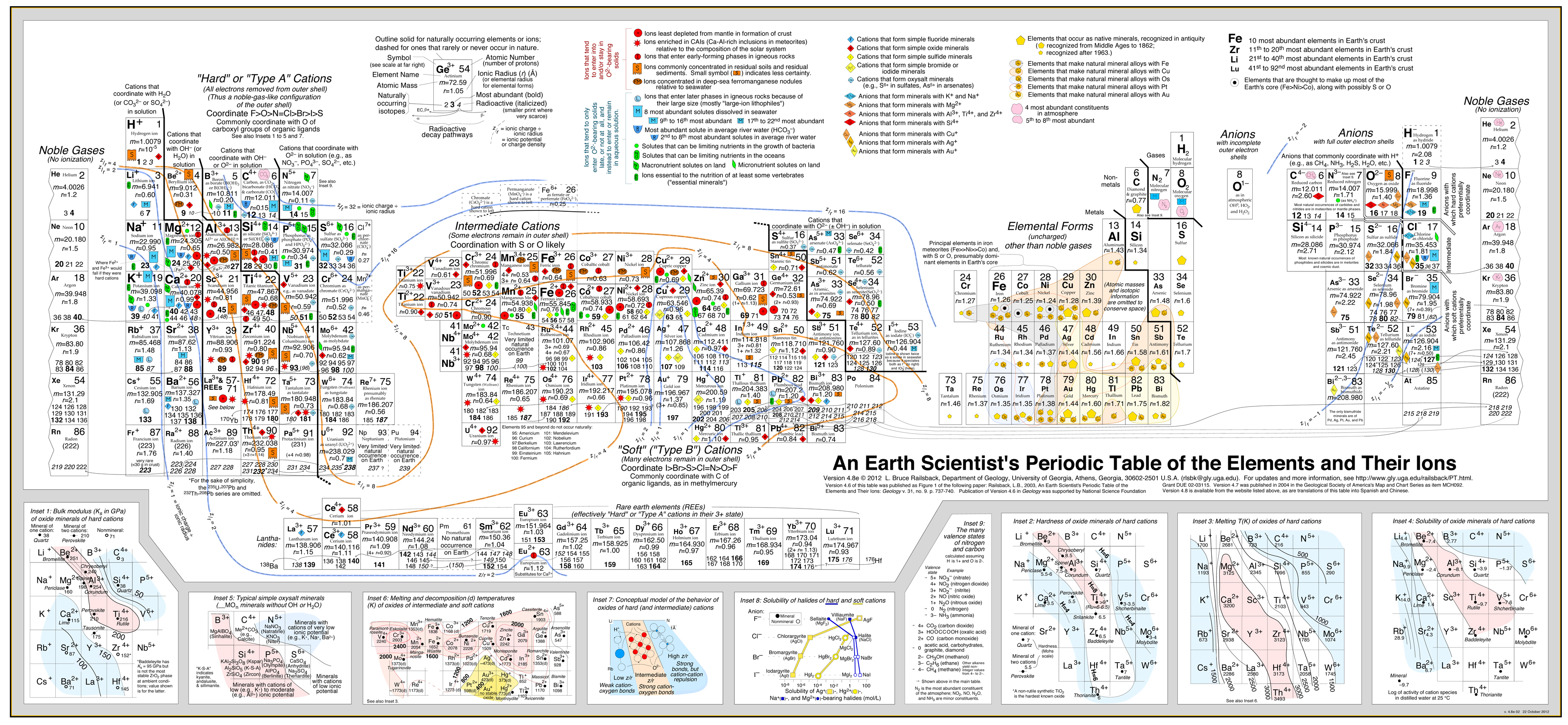
- The Railsback analysis uses
contours of behaviour superimposed upon the periodic table. [As Bruce told me in a personal communication: "Earth
scientists love contours..."].
- See the paper: A Synthesis of Systematic Mineralogy by Bruce Railsback that develops this analysis.
Pearson's HSAB Principle: The Hard Soft [Lewis] Acid Base Principle
Hard and Soft Acids and Bases, Ralph G. Pearson, J. Am. Chem. Soc. 1963, 85, 22, 3533–3539, https://doi.org/10.1021/ja00905a001
In the nineteen sixties, Ralph Pearson greatly expanded the Type A–Type B logic by explaining the differential complexation behaviour of cations and ligands in terms of electron pair accepting Lewis acids and electron pair donating Lewis bases:
Lewis acid + Lewis base → Lewis acid/base complex
Pearson classified Lewis acids and Lewis bases as hard, borderline or soft.
According to Pearson's hard soft [Lewis] acid base (HSAB) principle:
Hard [Lewis] acids prefer to bind to [complex with] Hard [Lewis] bases
and
Soft [Lewis] acids prefer to bind to [complex with] Soft [Lewis] bases
At first sight, the HSAB analysis seems rather similar to the Type A and Type B system.
However, Pearson classified a very wide range of atoms, ions, molecules and molecular ions as hard, borderline or soft, moving the analysis from traditional metal/ligand inorganic chemistry into – and combining with – the realm of organic chemistry.
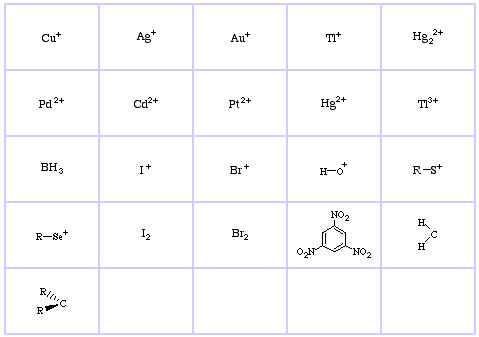
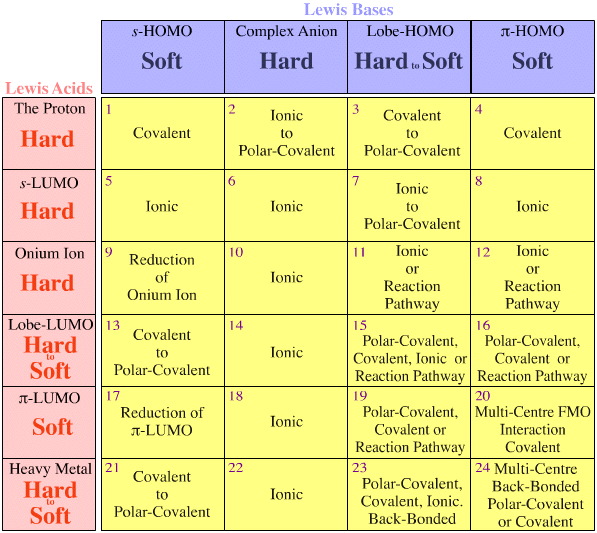
Pearson's HSAB Classification System, from here:
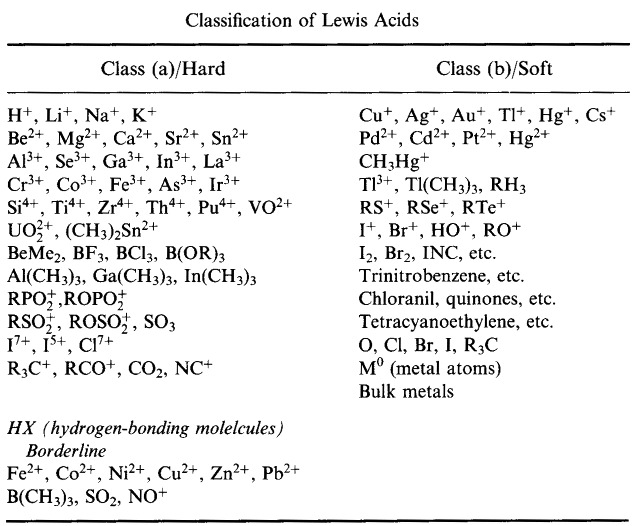
Pearson's Hard Lewis Acids (from the Chemical Thesaurus), here, and from the congeneric array database, here:
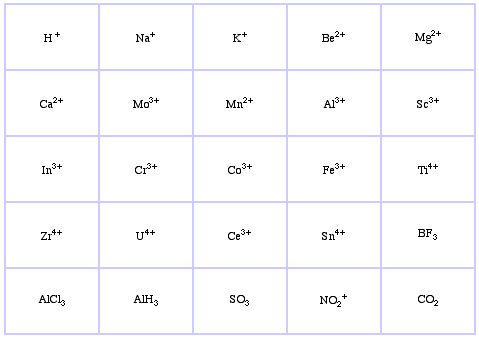
Pearson's Borderline Lewis Acids, here, and here:
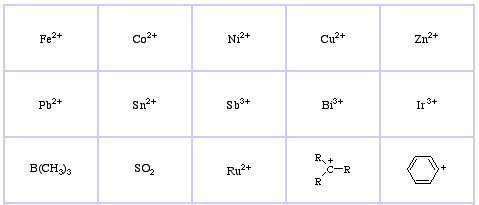
Pearson's Soft Lewis Acids, here, and here:
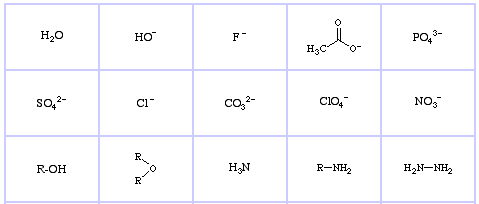
Pearson's Hard Lewis Bases (from The Chemical Thesaurus), here, and from the congeneric array database, here:
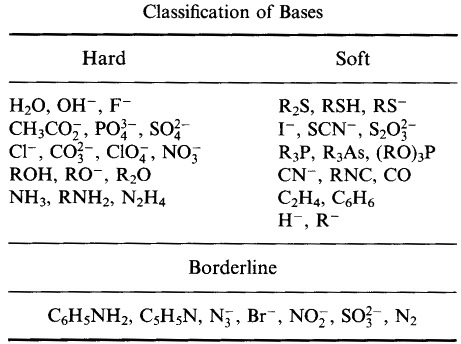
Pearson's Borderline Lewis Bases, here, and here:

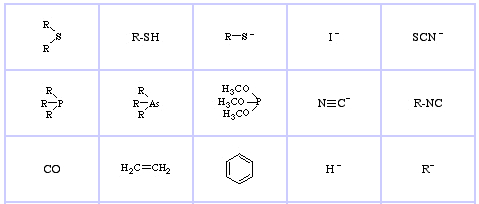
Pearson's Soft Lewis Bases, here, and here:
Jensen's Review
William (Bill) Jensen presented three papers in the ACS journal Chemistry, vol 47 (1974), Lewis Acid-Base Theory: Part I March pp 11-14; Part II April pp 13-18; Part III May pp 14-18.
The combined paper – which is both excellent and detailed – was available on Bill's webspace (the link is broken) however, a clone of the file can be downloaded from this website.
Part III deals with Pearson's HSAB analysis, which we critique on the next page of this web book.
Klopman's FMO Analysis
In 1968, G. Klopman attempted to quantify Pearson's HSAB principle using frontier molecular orbital (FMO) theory, as discussed elsewhere in this web book, here, with this equation:
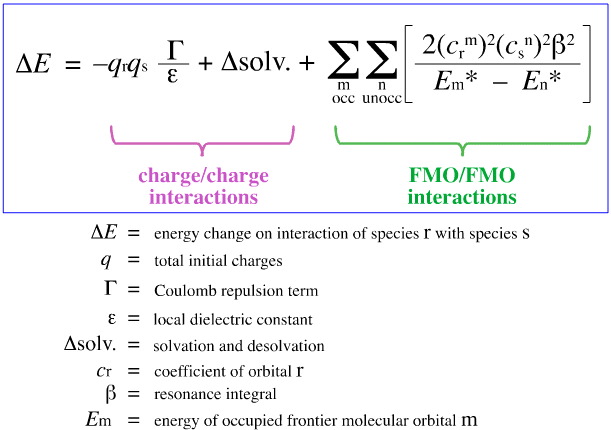
Klopman proposed that:
Hard [Lewis] Acids bind [complex] to hard [Lewis] bases to give charge-controlled (ionic) complexes. Such interactions are dominated by the +/– charges on the interacting species.
and
Soft [Lewis] Acids bind [complex] to soft [Lewis] bases to give FMO-controlled [covalent] complexes. These interactions are dominated by the energies of the participating frontier molecular orbitals (FMO), the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO).
Read more elsewhere in the Chemogenesis web book, here, or look at Ian Fleming's Organic Chemistry and FMO theory here, where these ideas are developed at some length.
Using the above analysis, the contributing aspects of charge-controlled and FMO-controlled Lewis acid/base complexation are separated and quantified, a crucial development.
Combining Pearson's and Klopman's Ideas
• Hard Lewis acids:
• Atomic centres of small ionic radius
• High positive charge
• Species do not contain electron pairs in their valence shells
• Low electron affinity
• Likely to be strongly solvated
• High energy LUMO• Soft Lewis acids:
• Large radius
• Low or partial δ+ positive charge
• Electron pairs in their valence shells
• Easy to polarise and oxidise
• Low energy LUMOs, but large magnitude LUMO coefficients• Hard Lewis bases:
• Small, highly solvated, electronegative atomic centres: 3.0–4.0
• Species are weakly polarisable
• Difficult to oxidise
• High energy HOMO• Soft Lewis bases:
• Large atoms of intermediate electronegativity: 2.5–3.0
• Easy to polarise and oxidise
• Low energy HOMOs but large magnitude HOMO coefficients• Borderline species have intermediate properties.
There is a qualifier in Klopman's paper saying that: it is not necessary for species to possess all properties.
The Ho Paper
Pearson suggested that hard-to-soft trends could be found amongst groups 15, 16 and 17 of the periodic table. In 1975 the idea was extended by Tse Lok Ho who used realistic chemical species and coined the term congeneric (of the same family), where congeneric species are isoelectronc (have the same outer shell Lewis structure).
[Your author has spent many, many hours reading this most interesting paper.]
 |
|||||
Bi |
Sb |
As |
P |
N |
Pearson, R.G., Hard and Soft Acids and Bases, JACS 85, 3533-3539 (1963) |
Te |
Se |
S |
O |
||
I |
Br |
Cl |
F |
||
R3Sb: |
R3As: |
R3P: |
R3N: |
Ho, T.-L., The Hard Soft Acids Bases (HSAB) Principle and Organic Chemistry Chemistry Reviews 75, 1-20 (1975) | |
H3C– |
H2N– |
HO– |
F– |
||
I– |
Br– |
Cl– |
F– |
||
H3C+ |
(CH3)H2C+ |
(CH3)2HC+ |
(CH3)3C+ |
||
The HSAB Principle for Organic & Main Group Chemists
For our purposes – main group and organic reaction chemistry – the Pearson approach is most successful when comparing pairs of species:
- Sodium ion, Na+, is harder Lewis acid than the silver ion, Ag+
- Alkoxide ions, RO–,
are harder Lewis bases than thioanions, RS–
- Copper(II) ion, Cu2+,
is harder Lewis acid than the copper(I) ion, Cu+
- The nitrogen anion end of
the ambidentate cyanide ion, CN–, is harder Lewis base than
the softer carbon anion end, NC–
- The ambidentate enolate ion, has a hard oxyanion Lewis base centre while the carbanion centre is softer Lewis base and is more nucleophilic
This type of analysis can be very useful in explaining reaction selectivity.
For example, β-propiolactone – a reactive cyclic ester – is ring opened by nucleophilic Lewis bases. The attack can occur at two positions and nucleophiles exhibit regioselectivity:
- Harder nucleophiles
like alkoxide ion, R-O–, attack the acyl (carbonyl)
carbon.
- Softer nucleophiles like the cyanide ion, NC–, and the thioanion, R-S–, attack the β-alkyl carbon.
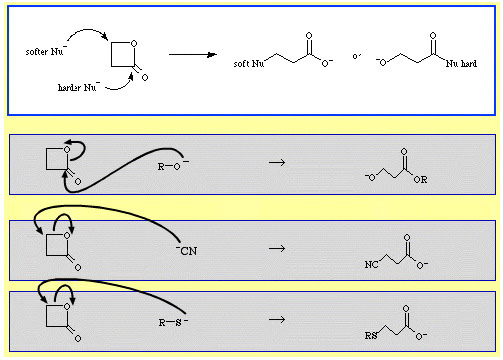
There are quite a number of examples of ambidentate selectivity in The Chemical Thesaurus reaction chemistry database:
Problems, problems, problems...
However, there are severe problems with Pearson's analysis. While the Pearson-Klopman HSAB model is not exactly wrong... it does grossly simplify [over simplify] the known reaction chemistry, as recognised by Ralph Pearson himself:
|
At the beginning of his 1997 book, Chemical Hardness, Wiley-VCH, pp 3-4, Ralph Pearson candidly writes: "With [the 'Hard-Soft'] nomenclature it is possible to make a simple, general statement:
"Note that this Principle is simply a restatement of the experimental evidence which led to [the classification system in the first place]. It is a condensed statement of a very large amount of chemical information. As such it might be called a law. But this label seems pretentious in view of the lack of a quantitative definition of hardness. "HSAB is not a theory, since it does not explain variations in the strength of chemical bonds. The word 'prefer' in the HSAB Principle implies a rather modest effect. "Softness is not the only factor which determines the value of ΔH° in the equation: A + :B → A:B "There are many examples of very strong bonds between mismatched pairs, such as H2, formed from hard H+ and soft H–. "H2O, OH– and O2– are all classified as hard bases, but there are great differences in their base strength, by any criterion." RP |
Indeed so... (!)
One problem is that the full set of hard-borderline-soft interactions and complexations is simply not considered using the Pearson analysis. Look how empty the HSAB interaction matrix is:
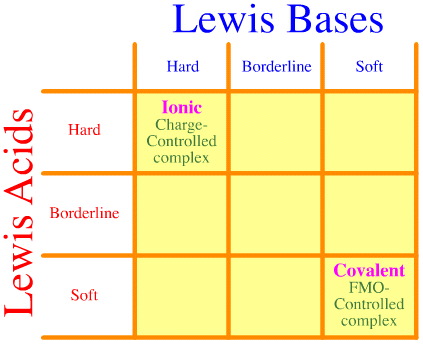
The Pearson HSAB principle states that "hard [Lewis] acids prefer to bind to hard [Lewis] bases and that soft [Lewis] acids prefer to bind to soft [Lewis] bases", which may be true, but it says nothing about mixed hard-soft complexes.
Klopman simply states – very unhelpfully – that such interactions are "undefined"!
Yet, many of the most interesting reagents of organic and inorganic reaction chemistry are hard-soft "strained" complexes:
| Sodium hydride |
NaH
|
Na+
|
H–
|
| Lithium aluminium hydride |
LiAlH4
|
Al3+
|
H–
|
| Lead(IV) acetate |
Pb(AcO)4
|
Pb4+
|
AcO–
|
| Methyl iodide | CH3I |
CH3+ |
I– |
| Methyl lithium |
CH3Li
|
Li+
|
CH3–
|
| Triethyloxonium tetrafluoroborate |
[Et3O]+ [BF4]–
|
CH3CH2+
|
:OR2
|
| Ferrocene |
Fe(Cp)2
|
Fe2+
|
[C5H5]–
|
|
Hard
|
Borderline
|
Soft
|
By comparison, the richness of known reaction chemistry arises naturally in the Lewis acid/base interaction matrix, a central tenet of the chemogenesis analysis (but we are in danger of getting ahead of ourselves, see the next pages here & here).
There are two observations/rules, and both concern congeneric arrays of isoelectronic/isoreactive species:
- Congeneric arrays are always found within the cells of the Lewis acid/base Interaction Matrix, and not crossing cells.
- Hard-to-soft trends occur within congeneric arrays, but they never cross between arrays.
Fajans' Rules
The Pearson-Klopman HSAB analysis is also in direct contradiction with the well known "Fajans' rules" (developed over the years 1915-24), even though no other author appears to have addressed this issue to date.
Ionic-covalent character in metal plus non-metal binary materials can be calculated using the Pauling equation, here, but the difference in electronegativity underestimates the effect of polarisation: the extent to which one atom distorts or polarises the electron cloud of the other.
Fajans rules say:
- A small positive
ion is highly polarising, favours covalency, and for a given cation
the covalent character increases as the anion becomes bigger.
- Large negative ions
are highly polarisible, favour covalency, and for a given anion covalent
character increases as the cation gets smaller.
- Covalent character
increases with increasing ionic charge on either ion.
- Polarisation, and hence covalency, is favoured if the positive ion does not have a noble gas configuration. This is important for cations like: Tl+, Pb2+, Bi3+, Ti3+, V3+, Cr2+, Mn2+, Cu+, Ce3+ & Eu2+.
An example:
Consider beryllium chloride, BeCl2 compared with the other alkaline earth chlorides: MgCl2, CaCl2, SrCl2, & BaCl2:
Cation |
Ionic Radius |
Eneg. |
% Ionic of to Cl– bond |
Bond & Material Type |
Be2+ |
41 |
1.57 |
34 |
Covalent/Molecular |
Mg2+ |
86 |
1.31 |
42 |
Ionic Salt |
Ca2+ |
114 |
1.00 |
51 |
Ionic Salt |
Sr2+ |
132 |
0.95 |
52 |
Ionic Salt |
Ba2+ |
149 |
0.89 |
54 |
Ionic Salt |
Ionic radius data from web elements
Beryllium chloride, BeCl2, is covalent: the anhydrous material is soluble in organic solvents, it sublimes (in a vacuum), and the molten material is a poor conductor of electricity. MgCl2, CaCl2, SrCl2 and BaCl2 are ionic materials and the molten salts are excellent electrical conductors.
- Fajans rules clearly explain this chemistry by saying that the very small, highly charged Be2+ ion is able to polarise (distort) the electron clouds of comparatively large chloride ions into covalent bonding and therefore to give a molecular structure.
- The Pearson-Klopman HSAB analysis states that the beryllium ion, being the smallest of the Group II metal cations is also the hardest. Beryllium ion salts should therefore exhibit extreme charge controlled bonding and give rise to ionic materials, but they do not.
- The chemogenesis analysis, here, says that Group II cations:
Be2+, Mg2+, Ca2+, Sr2+ &
Ba2+, make up a congeneric series of charged s-LUMO Lewis
acids, that linear behaviour trends are found over this series.
These linear behaviour trends can be ascribed to 'hard-soft' behaviour, if so wished, however, the terms 'hard' and 'soft' can only be used with respect to [and within] the congeneric series in question and 'hard-soft' comparisons cannot be made with respect to other Lewis acids.
So, What's Going On?
The point is that no physical parameter correlates with hardness over Pearson's chosen set of species. This creates ambiguities, such as with the organic chemistry of the fluoride ion, here, and the contradiction with Fajans' rules, above.
The Pearson model takes no account of FMO geometry (the shapes & phases of the participating orbitals). For example, just how similar are Pearson's hard [Lewis] acids:
H+ [NH4]+ BF3 CO2 Cs+ Cu2+ ?
Or, how similar are Pearson's soft [Lewis] bases:
H– R2S: H3C– benzene ?
Crucially for organic and main group chemists, the HSAB analysis says little/nothing about the important carbenium ion (carbocation) Lewis acid, H3C+, or the carbanion Lewis base, H3C–.
|
Bold Claim The one-dimensional hard-borderline-soft continuum of Pearson's analysis actually has the effect of blurring much of the rich, linear (predictable) behaviour that can be found in Lewis acid/base reaction chemistry space. The new chemogenesis analysis – as presented in this web book and backed by the reaction chemistry held in The Chemical Thesaurus database – avoids and explains the pitfalls of Pearson's much hyped HSAB approach. |
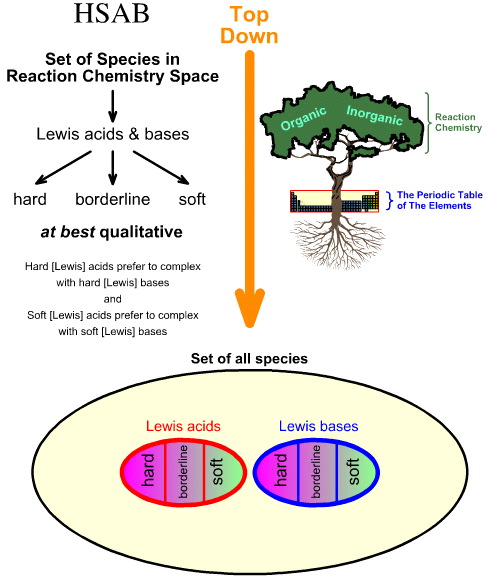
Comparing the "Top Down" HSAB Analysis with the "Bottom Up" Chemogenesis Analysis
Pearson's Hard Soft [Lewis] Acid Base (HSAB) analysis is top down.
- Starting with all
species in reaction chemistry space, a number of important species are
identified as Lewis acids and Lewis bases.
- Lewis acids and Lewis bases are then classified as hard, borderline or soft using empirical observation and the principle that: hard Lewis acids prefer to complex with hard Lewis bases and soft Lewis acids prefer to complex with soft Lewis bases:
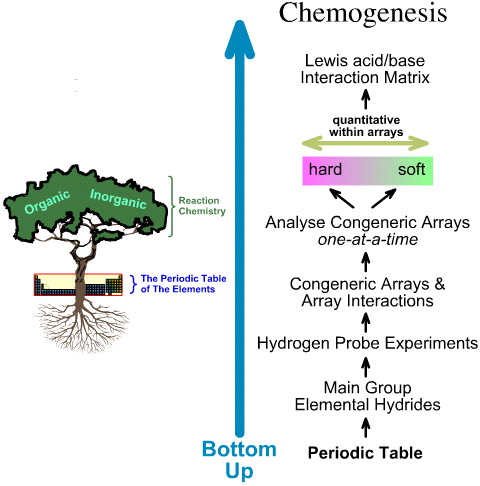
In contrast, the chemogenesis analysis is bottom up:
- The main group elemental
hydrides are subjected to the 5 hydrogen probe experiments.
- Congeneric arrays
and array interactions are studied.
- Linear hard-to-soft structural and reactivity trends are identified within arrays, and it
is recognised that linear behaviour cannot expected between arrays.
- Lewis acids and Lewis bases are classified by their Lewis electronic structures and FMO topologies and are arranged into a Lewis acid/base interaction matrix, here.
The HSAB Papers:
R.G.Pearson, J.Am.Chem.Soc., 85, 3533-3543, 1963
R.G.Pearson, Science, 151, 172-177, 1966
R.G.Pearson, Chem. Br., 3, 103-107, 1967
R.G.Pearson, J.Chem.Ed., 45, 581-587, 1968
R.G.Pearson, Chemical Hardness, Wiley-VCH (1997)G.Klopman and R.F.Hudson, Theoret. Chim. Acta, 8, 165, 1967
G.Klopman, J.Am.Chem.Soc., 90, 223-234, 1968Also look here.
Other Post-Pearson Analysis
The ECW model is a semi-quantitative model that describes and predicts the strength of Lewis acid/base interactions. Initially, the model assigned electrostatic (E) and covalent (C) parameters to the Lewis acids and bases. This was later expanded to the ECW model to cover reactions that have a constant energy term, W, which describes processes that precede the acid/base interaction.
In Drago & Wayland's original 1965 analysis, a two term equation was employed such that each Lewis acid is characterized by EA and CA terms and each Lewis base by EB and CB where the E and C parameters refer to the electrostatic and covalent contributions to the strength of the bonds that the acid/base interaction will form. (This is like the Klopman analysis, above.) These parameters were empirically obtained by using enthalpies for adducts that form only σ bonds between the Lewis acid and the Lewis base and have no steric repulsion:
−ΔH = EAEB + CACB
In the ECW model, a new term W was added to the equation.
-
−ΔH = EAEB + CACB + W
where the W term represents a constant energy for cleavage of a dimeric Lewis acid or Lewis base.
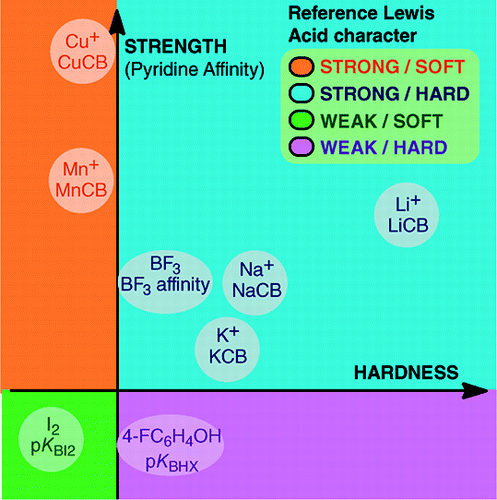
From An Overview of Lewis Basicity and Affinity Scales by Laurence, Graton & Gal: J. Chem. Educ. 2011, 88, 12, 1651–1657:
Abstract:
The impossibility of establishing a universal scale of Lewis basicity does not prevent the determination of the quantitative behavior of Lewis bases, thanks to scales constructed against particular Lewis acids: BF3, 4-FC6H4OH, I2, Li+, Na+, K+, Al+, Mn+, CpNi+, and CH3NH3+. These scales encompass important types of bonds formed in a Lewis acid–base adduct: the dative bond, the conventional and ionic hydrogen bonds, the halogen bond and cation–molecule bonds for metal cations of groups 1, 7, 10, 11, and 13. Moreover, although these scales are generally not interrelated, there exist family-dependent relationships that permit ranking, in a rather general order, of [Lewis] bases belonging to a given chemical family, for example, the family of oxygen bases. Therefore, the scepticism about the quantitative usefulness of the Lewis concept of acids and bases is no longer founded.and:
The formation of Lewis acid–base adducts covers a wide variety of bond-forming processes, from the weak van der Waals bond in Ar---BF3 to the strong dative bond in H3N–BF3. The term "bond" can be objectionable for weak adducts. These weakly bonded species are generally produced in a supersonic beam or a cryogenic matrix. Here, we are mainly interested by complexes that can be observed in a room temperature mixture of the Lewis acid and of the Lewis base.In water, the order of complexation constants of halide ions with the acid Fe3+ is F– > Cl– > Br– > I–, whereas with Hg2+, it is I– > Br– > Cl– >F–. This reversal is explained by the hard and soft acid and base principle of Pearson.
The coordination of a series of azines to metallocenes has been correlated to the hydrogen-bond basicity scale of the azines.
The ab initio computation of the Lewis acid strength of covalent metal halides in vacuo using the fluoride anion as the reference Lewis base.
A DN value of triethylamine was estimated from a correlation between DN and the NMR chemical shift of the 23Na nucleus for solutions of sodium salts in basic solvents. Later on, the direct determination gave a value that was half the estimated value.
 |
 |
 |
| Lewis & Brønsted Theories of Acidity | Main Group Elemental Hydrides |
© Mark R. Leach 1999 –
Queries, Suggestions, Bugs, Errors, Typos...
If you have any:
Queries
Comments
Suggestions
Suggestions for links
Bug, typo or grammatical error reports about this page,please contact Mark R. Leach, the author, using mark@meta-synthesis.com
This free, open access web book is an ongoing project and your input is appreciated.