Periodic Table |
 |
 |
 |
 |
 |
 |
 |
| Pericyclic Reaction Chemistry | Thermochemistry Synthlet |
Why Do Chemical Reactions Occur?
The chemogenesis analysis presented in this web book is concerned with chemical reactions and reactivity with an emphasis on the nature of mechanism, but this narrative skirts around the fundamental question: why do chemical reactions happen at all?
The "why" question can be addressed at two levels, by looking at the thermochemistry of bulk materials and by examining at what is going on at the atomic level and the atom's quest for spherical symmetry.
Thermochemistry of Reacting Substances
Taking the macroscopic and view that chemistry involves the transformation of bulk substance, we can confidently state that a chemical process (reaction or interaction) can feasibly occur when the Gibbs free energy of the system decreases, ie. when ΔG is negative or less than zero, ΔG < 0.00.
The Gibbs function is: ΔG = ΔH – T ΔS
- Δ (delta) means "change in"
- ΔH is the change in enthalpy or heat equivalent
- T is the thermodynamic temperature, the temperature in Kelvin
- ΔS is the change in entropy or "dispersion of energy", where gases are more dispersed and have greater entropy than liquids, etc.
- Reactions can be exothermic, –ΔH, or endothermic, +ΔH
- Reactions [the
local system] can decrease in entropy, –ΔS,
or they can increase in entropy, +ΔS
- For a reaction to occur the Gibbs free energy must be negative: ΔG < 0.00
- ΔH⦵, ΔS⦵ & ΔG⦵ refer to standard conditions (1.0 atm) and temperature (298K)
- ΔH°, ΔS° & ΔG° refer to standard conditions but non-standard temperatures
The Gibbs function, ΔG = ΔH – TΔS, tells us that the entropy term, ΔS, is multiplied by the thermodynamic temperature, T, so the energy dispersion contribution (randomness) becomes progressively ever more important as the temperature is increases.
The Gibbs function tells us that there is a balance between: entities coming together and evolving heat, and heat being added to a collection of entities which makes them disperse.
- At high temperature: solids melt, liquids boil, bonds break and materials dissolve in solvents.
- At low temperature: gases condense, liquids freeze,bonds form and saturated solutions yield crystals.
A Couple of Qualifiers
There may be a substantial activation energy that stops a thermodynamically feasible reaction from occurring.
Trinitrotoluene, TNT, can feasibly explode with a great deal of energy into the hot gases CO2, H2O, N2, NO2... etc., but at room temperature the material is [said to be] meta-stable.
Thus, reaction processes can appear to violate the ΔG < 0 rule.
Consider crystallisation.
The crystal is more ordered than the melt/solution so entropy decreases and so surely, ΔG must be positive???
However, this analysis does not describe the thermodynamics of the system. Crucially heat is evolved and this must be lost (dispersed) to the surroundings so ΔG is negative at low temperatures. Apparent violations to the the ΔG < 0 rule are always a "local". Overall here is always an increase in entropy when the surroundings are included as part of the system.
Indeed, life on Earth is highly ordered and appears to be in violation of thermodynamics. But, we are part of the Earth/Sun system. As the Sun 'runs down' it gives out photons of light which power photosynthesis and life on our green planet.
That said, it is possible to design and build real world chemical reaction systems using glass & metal that remove heat and/or products. The effect is to separate and isolate the local system from the global system.
If these issues are not pointed out, much of the following discussion could be highly ambiguous.
The Gibbs function can be used to show how water and stream interact at 50°C and 1.0 atm pressure:
The enthalpy of formation and entropy data for liquid water and steam are both and can be looked in tables. The data on both sides of the reaction is summed, and the left-hand-side (reactant) data is subtracted from the right-hand-side (product) data. For this reaction process this gives, ΔHreaction = +44.0 kJ/mol and ΔSreaction = +0.119 kJ/Kmol.

Choose a temperature, say 50°C (323 Kelvin), plug the numbers into the Gibbs function and calculate the free energy of the system:

At 50°C (323 Kelvin), the Gibbs free energy is +5.6 kJ/mol, so the reaction will NOT proceed, in fact it will go in the reverse direction. As is well known, at 50°C and 1.0 atm steam condenses to water.
At equilibrium ΔG = 0. In this state the Gibbs relationship can be rearranged to T = ΔH/ΔS, an equation that tells us the temperature at which, in this case, water will boil. Even this rather simplistic version of the Gibbs equation predicts 370K or 97°C... really quite close to 100°C... and this is not a full thermochemical calculation.
Consider the classic and industrially important Haber Process for the synthesis of ammonia.
3 H2(g) + N2(g) ⇄ 2 NH3(g)
Interesting factoid: 1% of the world's energy supply is consumed in the manufacture of ammonia derived fertilizer and other chemicals, Science 297(1654), Sept 2002.
The process operating conditions are a balance between:
Overcoming the activation energy of the reaction
Having a sufficient rate of reaction rate
Moving the equilibrium position to the production of ammonia
The cost of the industrial plant
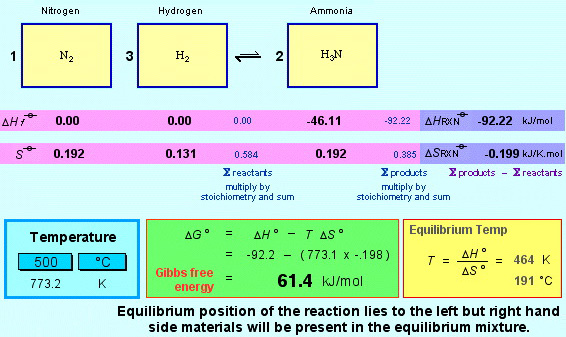
The Gibbs function allows us to model and understand numerous thermal reactions and processes, it tells us a great deal about the entropy – the dispersion of energy ΔS – and its relationship with temperature T.
The Gibbs function explains how we can manipulate reaction systems so that they produce chemical substances that are not in thermodynamic equilibrium with their surroundings.
Consider the production of quick lime (calcium oxide, CaO) from limestone, one of the world's oldest and in terms of scale one of the largest, chemical processes:
CaCO3(s) ⇄ CaO(s) + CO2(g)
The production of quicklime illustrates the general principle of: heat, separate, cool quickly.
Heat the reactant substance(s) so that there is a change in phase space. High temperature means that the change occurs quickly. When calcium carbonate, CaCO3(s), is heated to high temperature the equilibrium position changes to carbon dioxide, CO2(g), plus calcium oxide, CaO(s).
Separate the phases. In the quick lime process, the hot carbon dioxide is gas is easily removed from the local system by venting to atmosphere.
Quickly cool the system, so trapping the various components in what is now an out-of-thermodynamic-equilibrium state.
In the quick lime case, the calcium oxide, CaO, is removed and placed in gas & water proof containers. At room temperature if calcium oxide comes into contact with carbon dioxide it will slowly react to reform calcium carbonate and if it comes into contact with water it forms slaked lime (calcium hydroxide), Ca(OH)2.
This type of process relies on the general principle that the time scale for thermodynamic equilibration is longer than the time it takes to physically separate the phases. This is achieved through manipulation of the reaction system using good design and operation procedures.
OK... What's In It For The Atoms?
The Gibbs function tells us about the dispersion of phases at various temperatures: how the entropy, ΔS, of the system is influenced by temperature, but it says nothing about the nature of the ΔH bonding term. It does not in any way explain why the atoms choose to react in the various ways that they do.
So, what is in it for the atoms?
Taking Occam's Razor to The Set of Chemical ReactionsWilliam of Occam (1285-1349) emphasised that it is important to get to point, to strip away all of the unnecessary detail and to deal with the core of the issue at hand. Or, as William eloquently put it:
To find the answer to the question why do chemical reactions occur?, it is necessary to take Occam's razor to the set of chemical reactions and to look for the few, simple, illuminating ideas and examples amongst the morass of interesting but complicating detail. |
Electronegativity
In his book Modern Inorganic Chemistry, William Jolly states:
"The most stable arrangement of [polar] covalent bonds connecting a group of atoms is that arrangement in which the atom with the highest electronegativity be bonded to the atom with the lowest electronegativity." Jolly, Modern Inorganic Chemistry, McGraw-Hill (1985) pp 61-62 |
Jolly gives four examples to illustrate this general principle. In each case there is a net increase in electronegativity difference:
Hydrogen iodide reacts with chlorine to give hydrogen chloride and iodine:
2HI + Cl2 → 2HCl + I2
Chlorine reacts with iodine to give the interhalogen compound iodine chloride, ICl:
Cl2 + I2 → 2ICl
There is a ligand exchange reaction between boron tribromide and phosphorus trichloride to give boron trichloride and phosphorous tribromide:
BBr3 + PCl3 → BCl3 + PBr3
Titanium tetrachloride reacts with alcohols to give the titanium tetraalkoxide and hydrogen chloride:
TiCl4 + 4 R-OH → Ti(OR)4 + 4HCl
Here are the four reactions with their respective electronegativity calculations:
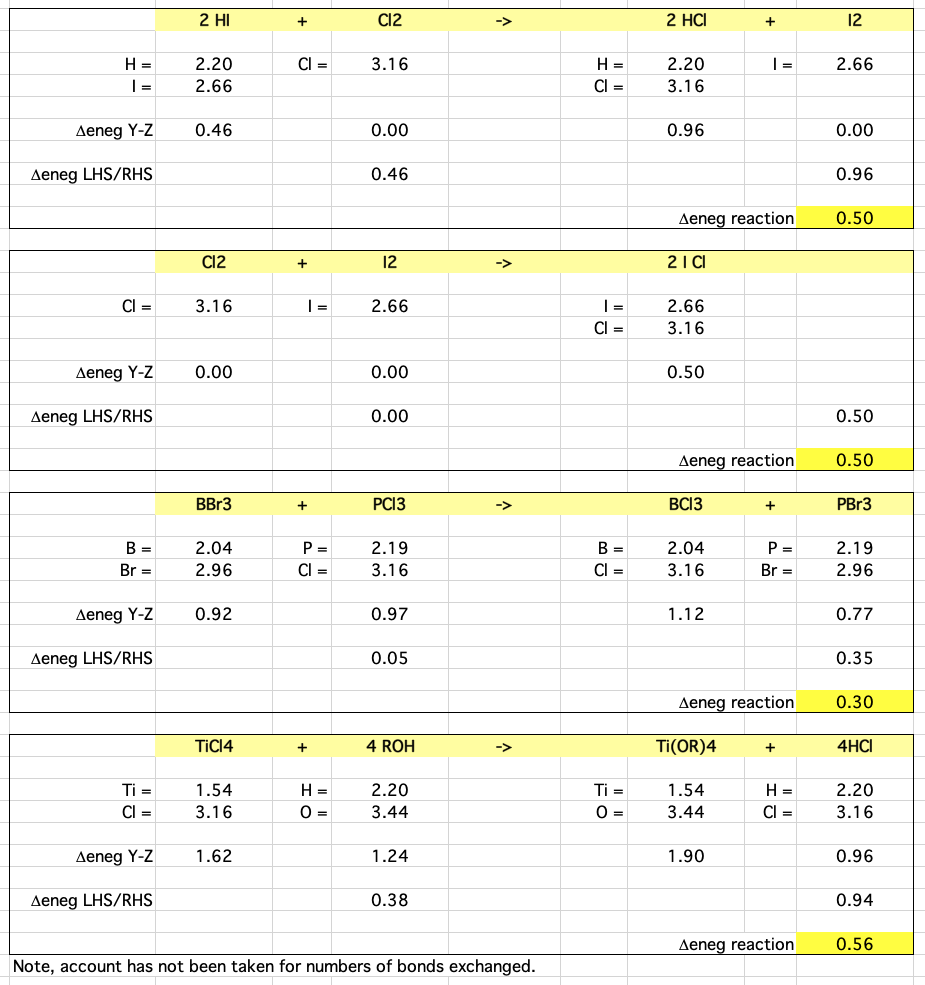
Revised Pauling electronegativity data is used. Download the Excel Spreadsheet here.
Another example:
Sodium hydride, NaH, reacts with boron trifluoride, BF3, to give sodium borohydride,NaBH4 and sodium fluoride, NaF, indeed this reaction is used in the industrial synthesis of NaBH4:
4NaH + BF3 → NaBH4 + 3NaF
In this reaction the electropositive sodium, Na = 0.93, moves from an association with hydrogen, H = 2.20, to an association with fluorine, F = 3.98. And 'in the other direction', boron, B = 2.04, moves from F = 3.98 to H = 2.20.
Disproportionation of Difluoromethane
This author's choice for the reaction that most clearly illuminates what's in it for the atom is the disproportionation of difluoromethane, CH2F2, to methane, CH4, and tetrafluoromethane, CF4.
This reaction reinforces the maximisation of electronegativity difference, but it shows something else as well: maximisation of spherical symmetry.
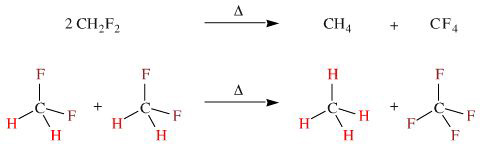
This reaction can be considered can be considered thermochemically:
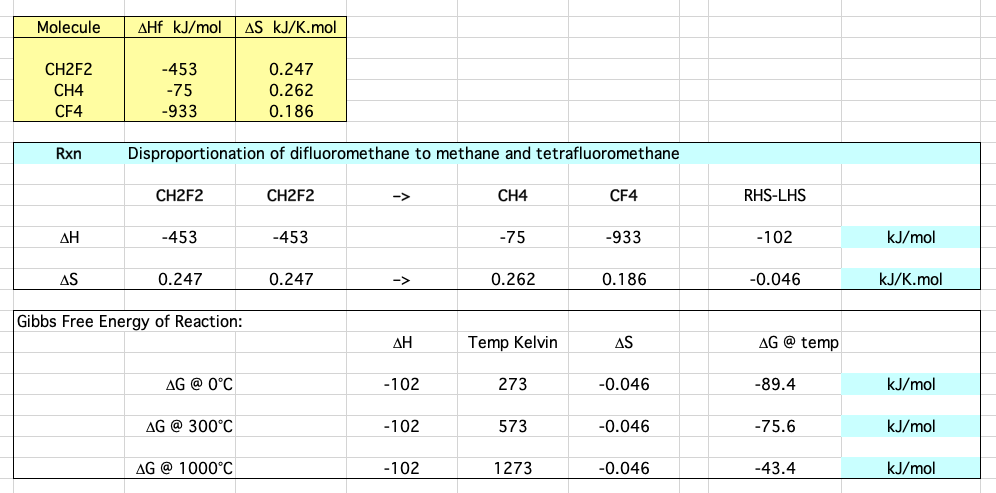
Download the Excel spreadsheet here.
The reaction system is particularly simple because:
- All species are molecular and in the gas phase.
- The reaction proceeds under thermal conditions and equilibrium is reached.
- The reaction is clearly exothermic, ΔHrxn = -102 kJ/mol.
- ΔG is negative at all temperatures.
- To good approximation, the ΔS enthalpy term is negligible in most disproportionation reactions and can be ignored.
Another example: On heating formaldehyde (methanal) disproportionates to methane and carbon dioxide:
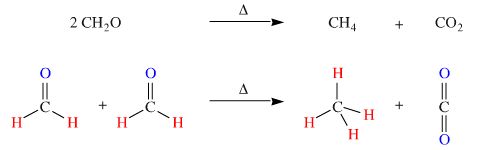
For organic chemists, this is the 'parent example' of the Cannizzaro reaction, a reaction that involves the disproportionation of an aldehyde into a primary alcohol and a carboxylic acid.
The products, methane and carbon dioxide, have higher spherical symmetry than the aldehyde starting material.
A third example, but this time a ligand exchange rather than a disproportionation reaction. When heated together, trifluoroiodomethane reacts with fluoromethane to give tetrafluoromethane and methyl iodide.
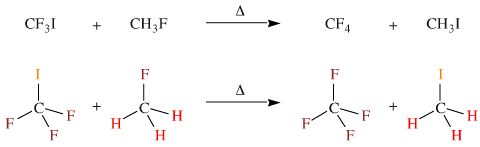 In 1967 Ralph Pearson cited these
three reactions in support of his (then new) HSAB principle, saying:
In 1967 Ralph Pearson cited these
three reactions in support of his (then new) HSAB principle, saying:
"The symbiotic principle states that there is an extra stabilisation if several soft bases (ligands) or several hard bases cluster about a single acidic atom." Pearson & Songstad, JACS, 89, 1827 (1967). [Read more about Pearson's HSAB principle look elsewhere in this web book.]
In this author's opinion, these reactions show no such thing. What they do show is general and far more interesting: if an atomic centre has multiple ligands/bonding partners, then the atomic centre prefers to have similar ligands rather than mixed bonding partners.
Indeed, it appears to be general that:
| Atomic centres behave so as to maximise their spherical symmetry. |
Spherical symmetry can be defined (from Symmetry: A Unifying Concept by István & Magdolna Hargittai):
"Everything is the same in all directions, as if on the surface of a sphere."
The pollen of hollyhock exhibits good spherical symmetry:
A CSIRO scientist examines a 'perfect' silicon sphere, similar to one that will be used to determine the exact atomic weight of a kilogram, from The Age:

Maximizing Spherical Symmetry: Molecular Orbitals
Consider again the species involved in the 2 CH2F2 → CH4 + CF4 disproportionation reaction:
Methane, CH4, and tetrafluoromethane, CF4, are perfect tetrahedral octapoles: they have zero dipole moment and belong to Td the symmetry point group.
Difluoromethane, CH2F2, has a dipole moment of 2.29 debyes (calculated) and the molecule belongs to the C2v symmetry point group.
The HOMO and LUMO frontier molecular orbitals are clearly more spherically symmetric in CH4 and CF4 compared with CH2F2:
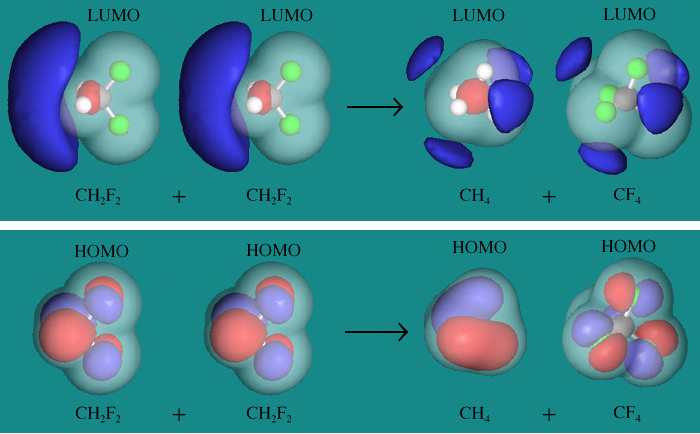
Compare the HOMO of CH2F2 with the HOMOs of CH4 and CF4. The CH4 and CH4 HOMOs are clearly have more spherical symmetry than the CH2F2 HOMO. It is the same with the LUMOs. Diagrams obtained using Spartan.
|
The observation that atoms strive to achieve spherical symmetry should not be unexpected because it can be seen with the simplest chemical systems, including isolated atoms. Indeed, an atom's quest for spherical symmetry is a dominant theme in chemistry. |
Maximising Spherical Symmetry: Atomic Orbitals
Consider the electronic structure of atoms. Electrons add to atoms according to a few simple rules:
- The Pauli exclusion principle states that an orbital can contain a maximum of two electrons that must be of opposite spin.
- The Aufbau or build-up principle states that electrons enter and fill lower energy orbitals before higher energy orbitals.
- Hund's rule states that when there there are degenerate (equal energy) orbitals available, electrons will enter the orbitals one at a time and only when all the orbitals are half filled will pairing-up occur.
- These rules act so as to maximise the spherical symmetry of the atom. The spherical s-orbitals fill before the dumbell-like p-orbitals, and the dumbell-like p-orbitals fill with electrons one-at-a-time before pairing up:
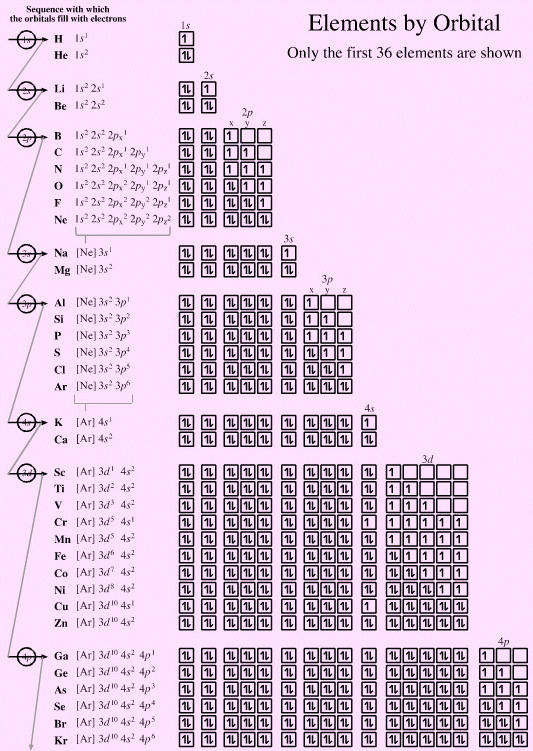
Nitrogen as 1s2 2s2 2px1 2py1 2pz1 is more spherically symmetric than 1s2 2s2 2px2 2py1 2pz0
Copper as [Ar] 3d10 4s1 is more spherically symmetric than [Ar] 3d9 4s2
Maximising Spherical Symmetry: Valence Shell Electron Pair Repulsion
Consider the valence shell electron pair repulsion, VSEPR method.
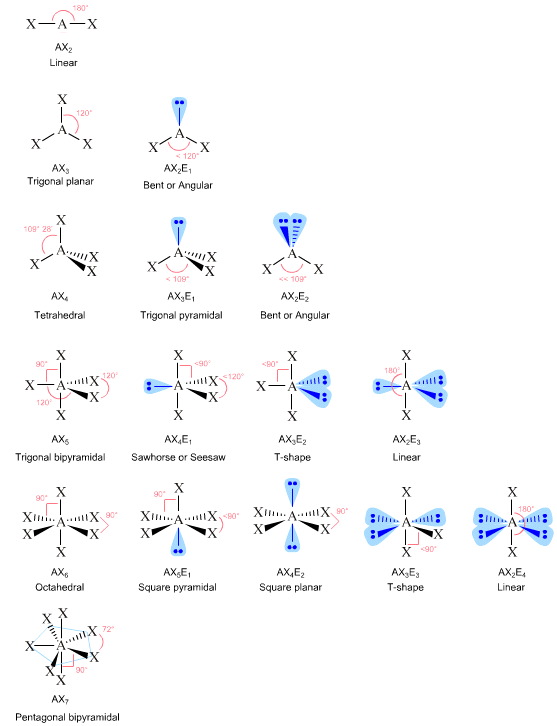
In this technique, bonding and non-bonding ("lone-pairs") of electrons are arranged about the atomic centre so as to maximise the spherical symmetry. Interestingly, nature adopts the same strategy, the maximisation of spherically. Thus, the VSEPR method can be used to predict molecular and ionic shape rather well.
Read more about VSEPR elsewhere in this web book.
Maximising Spherical Symmetry: Disproportionation
Atom centres with multiple ligands adopt the most spherically symmetric conformation, as predicted by VSEPR. Likewise, atomic centres with mixed ligands undergo exchange reactions to maximise spherical symmetry. |
Thus, on heating difluoromethane, CH2F2, disproportionates to methane, CH4, and tetrafluoromethane, CF4 because methane, CH4, and tetrafluoromethane, CF4, are more spherically symmetric than difluoromethane, CH2F2.

The ΔH enthalpy term of the Gibbs function, or what's in it for the atom, concerns the maximisation of atomic spherical symmetry.
Maximising Spherical Symmetry: Co-operation, Winners & Losers
Atoms in molecules and materials co-operate and compete so as to maximise the net atomic spherical symmetry. In a reaction there may be winners as losers, although the winners will always win more than the losers lose.
An example:
Aluminium chloride, AlCl3, reacts with alkyl chlorides, R-Cl, to give tetrachloroaluminate ion, [AlCl4]–, and a carbenium ion (carbocation), [R-CH2]+. The reaction is used in the first step of the Friedel-Crafts alkylation reaction.
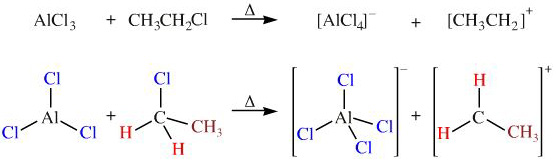
In this reaction the trigonal planar aluminium chloride Lewis acid, AlCl3, gains more spherical symmetry on going to the tetrahedral tetrachloroaluminate ion, [AlCl4]–, than the alkyl chloride, R-CH2Cl, looses on forming a carbenium ion, [R-CH2]+.
Pauling's Five Rules for Crystal Structure
The crystal structure of an ionic compound can be predicted using a set of empirical rules that act to maximise spherical symmetry about as many centres as possible:
- The First Rule: Around every cation, a coordination polyhedron of anions forms, in which the cation-anion distance is determined by the radius sums and the coordination number is determined by the radius ratio.
- The Number of Polyhedra with a Common Corner - The Electrostatic Valence Rule: An ionic structure will be stable to the extent that the sum of the strengths of the electrostatic bonds that reach an anion equals the charge on that anion.
- The Sharing of Polyhedra Edges, Faces & Corners, particularly faces by two anion polyhedra, decreases the stability of a crystal.
- An extension of the third rule: In a crystal which contains different cations, those with high charge and low coordination numbers tend not to share elements of their coordination polyhedra.
- The Rule of Parsimony The number of essentially different kinds of constituents in a crystal tends to be small.
Crystal structures are usually named after a definitive crystal structure, such as: zinc sulfide (structure), sodium chloride, cesium chloride, calcium fluoride (fluorite), rutile, diamond, etc.
Read more in the Wikipedia and ScienceWorld.
Mechanism and The Kinetic Domain
Consider again the 2 CH2F2 → CH4 + CF4 disproportionation reaction, and ask the question: Are there any possible competing reactions?
There is one: the carbon forming, or coking reaction, producing of hydrogen fluoride and carbon.
CH2F2 → C + 2HF
Thermochemistry calculations show this pathway is energetically preferred over disproportionation:
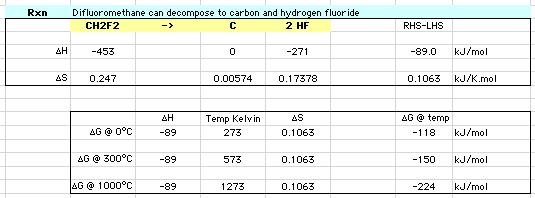
At 300° ΔG for disproportionation is -76 kJ/mol and for carbon + HF formation is -150 kJ/mol.
Download the spreadsheet.
Yet the 2 CH2F2 → CH4 + CF4 disproportionation reaction occurs.
So, the question is:
Why does CH2F2 disproportionate to CH4 + CF4 and not to C + 2HF?
The answer is subtle:
- When there are two or more possible reactions, each reaction will proceed by an associated reaction mechanism and each mechanism will have an associated activation energy, Eactiv., AND a Gibbs free energy, ΔGrxn.
- Under local conditions, the reaction will always proceed via the mechanistic pathway that has the lowest activation energy, Eactiv..
- The effect is to produce the locally thermodynamically more stable product(s) rather than globally most thermodynamically stable product(s).
At a higher temperature the globally most stable reaction will happen, and 'coking' will occur:
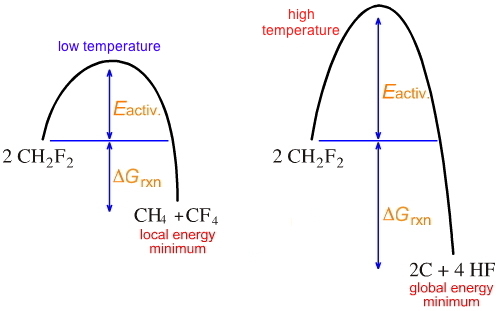
This is an important industrial limitation. Chemical engineers will 'push' the conditions to maximise yield [or 'mass transfer', in their language] but at the expense of carbon depositing on hot surfaces.
Chemoselectivity
The arguments given above have only concerned thermal equilibria: heat, pressure & concentration.
There also exist other types of chemical reactivity which exhibit subtle selectivities.
In photochemical reactions a photon of specific energy is adsorbed by a specific chemical entity creating a population inversion (in thermochemical terms) of excited species. Interesting & complex chemistry invariably ensues...
A classic example is the formation of ozone, O3:
O2 + UV light → 2 O•
O• + O2 → O3
Ozone is meta-stable, and so is thermodynamically unstable with respect to normal oxygen, triplet O2:
ΔfH O3 = +142.3 kJmol-1
The reaction:
3O3 → 3O2
Is exothermic and dispersion increases. This reaction is spontaneous/feasible at all temperatures.
Thus, O3 cannot be formed thermally from O2, but it can be formed photochemically.
Likewise, strange and interesting chemical selectivities are associated with Lewis acid/base, redox & pericyclic reaction chemistries.
All Rivers Flow To The Sea...
The Gibbs equation can predict whether a particular reaction is thermodynamically feasible and it can be used to compare reactions, but it tells us nothing about other possible possible reactions or the activation energies of those reactions.
The topology of this complex space must be determined by experiment.
A physical geography example illustrates this crucial point:
 |
And so it is with chemistry:
Chemical reactivity is dominated by the mechanistic & thermochemical topology of the local reaction chemistry space. |
Thus, this Chemogenesis web book is primarily concerned with the nature of mechanism and complexity.
 |
 |
 |
| Pericyclic Reaction Chemistry | Thermochemistry Synthlet |
© Mark R. Leach 1999 –
Queries, Suggestions, Bugs, Errors, Typos...
If you have any:
Queries
Comments
Suggestions
Suggestions for links
Bug, typo or grammatical error reports about this page,please contact Mark R. Leach, the author, using mark@meta-synthesis.com
This free, open access web book is an ongoing project and your input is appreciated.