Periodic Table |
 |
 |
 |
 |
 |
 |
 |
| Diatomics | Organic π-Systems & Functional Groups |
Polyatomic Species: Molecular Orbitals
Polyatomic species like methane, CH4, can be described in terms of molecular orbital theory, however, the diagrams can be very difficult to visualise. However, structures built up from hybrid atomic orbitals are much easier comprehend.
Introduction: Methane, CH4
Using the carbon and hydrogen atomic orbitals, methane, CH4, is constructed by overlapping the carbon's one 2s and three 2p AOs with the four hydrogen 1s AOs.
Methane's MOs have a topology similar to the AOs of carbon, but the structure can be very difficult to visualise, so the methane MO construction diagrams A, B and C (below) are shown with the AOs and MOs superimposed upon line structures of the methane. But, remember that the lines are "not there", it is the bonding MOs that hold the molecule together.
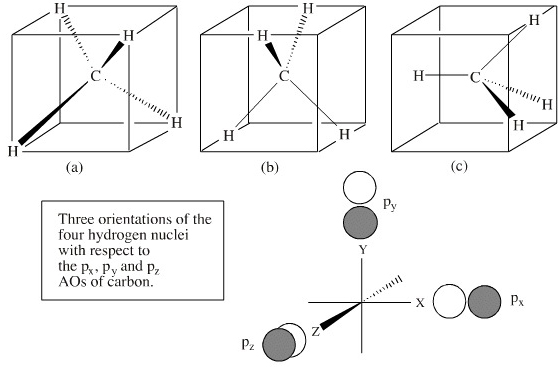
It is possible to devise an infinite number of MO methane constructs depending upon how the five nuclei (which are tetrahedral with respect to each other, with the carbon at the centre) are positioned in space with respect to the x, y and z Cartesian axes defined px, py and pz orbitals. On other words, the four hydrogen atoms can be regarded as sitting on a hypothetical spherical shell which is able to freely rotate with respect to the p orbitals.
We shall examine three methane LCAO MO constructions: A, B and C below.
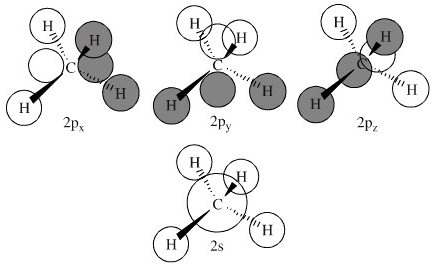
MO Methane: Construction A
In construction A, the three MOs derived from the carbon's three p orbitals are degenerate, as are the four hydrogen AOs, but it is not entirely obvious how any of the hydrogen AOs are overlapping with the carbon AOs. The hydrogens appear to be avoiding overlap with the p orbitals. Note, however, that these LCAO diagrams are schematic, drawn to emphasize LCAO construction rather than attempting to represent the orbital overlap integral. |
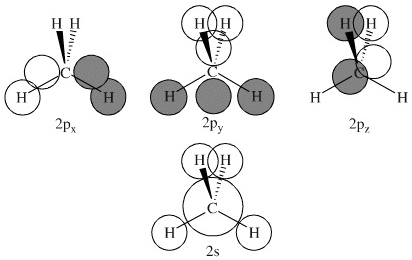
MO Methane: Construction B
In construction B, the 2px and 2pz orbitals overlap (are bonding) with respect to only two on the hydrogens, the other two hydrogens are on a nodal plane. The nodal plane is non-bonding with respect to these two hydrogens. The 2py AO is bonding with respect to all four hydrogen AOs. |
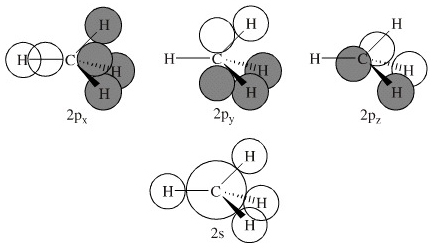
MO Methane: Construction C
In construction C, the 2px AO has maximum overlap with one of the hydrogen atoms, but at the expense of overlap with the other hydrogens and the other p orbitals. The three p orbitals also appear to be non-equivalent and therefore non-degenerate. Many authors explain the s H-C bonding in methane in terms of 1s + 2px (construction c) overlap. The apparent difficulties with each of the LCAO constructions disappear when it is realised that the net carbon-hydrogen orbital overlap integral in methane is the same for any spatial orientation of the hydrogen nuclei with respect to the 2px, 2py and 2pz orbitals. |
Molecular orbital calculations using software such as Spartan or Gaussian are performed by assigning the five nuclei positions in space, and then constructing wavefunctions for (or adding electrons into) the molecular orbitals, where the MOs are constructed as a linear combination of the contributing atomic orbitals, the LCAO approximation. Inter-nuclear geometries are varied until the energy is minimized:
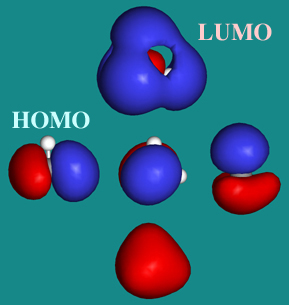
Ethane
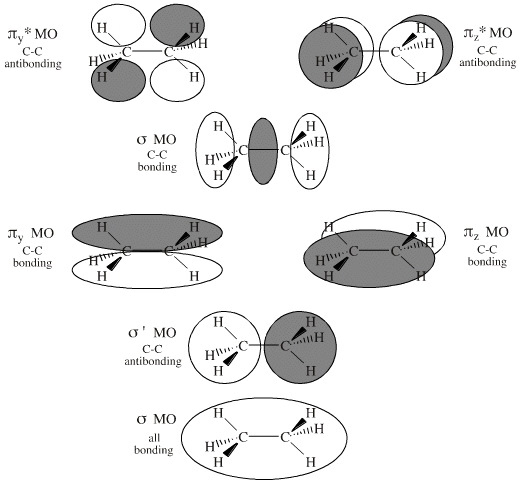
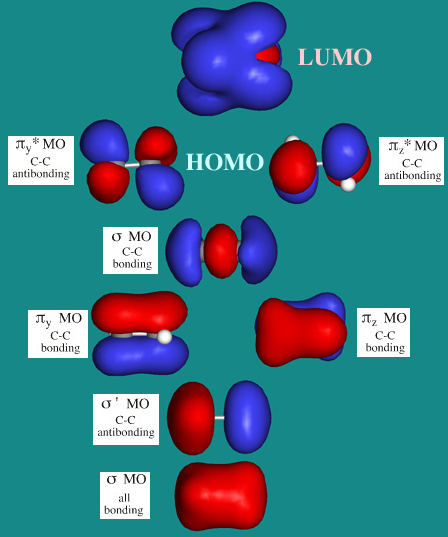
For symmetry reasons, the MOs of ethane, CH3CH3, are rather different to those of methane as the π-bonds and π*-antibonds are present.
Ethane possesses 8 atoms, 14 (valence) electrons and 7 MOs (four bonding and three antibonding). These larger numbers mean that it is easier to visualise ethane with preconstructed MOs, rather than attempting to show the full AO to MO construction.
- Carbon-carbon sigma
bonding primarily arises from an (end-on/end-on) px + px -> sigma MO. This is the first (and lowest
energy) ethane MO, the 1sigma MO.
- This C–C sigma
bonding is counteracted by an antibonding 1sigma* MO, although this
MO is bonding with respect to the hydrogen atoms.
- Superimposed upon
the 1sigma and 1sigma* MOs are a degenerate pair of bonding πy and πz MOs, but these are counteracted (again along the C-C bond axis) by a
degenerate pair of antibonding πy*
and πz*
MOs.
- Sitting (in energy)
between the π
and π*
MOs is the px/px sigma MO.
- Thus – as
a first approximation – the only MO which net bonds the two
carbon atoms together is the sigmax MO formed
by the end on interaction of the two px carbon
AOs. The carbon-carbon bond of ethane is a typical carbon-carbon single
bond and can rotate freely.
Ethene (Ethylene)
Ethene, H2C=CH2, has six atoms and 12 valence electrons in six MOs.
There are three sigma MOs (two bonding and one antibonding) which are similar to the equivalent MOs in ethane, but the π MOs are rather different.
- The πz bonding MO is counteracted by a πz*
antibonding MO.
- This leaves the highest
energy bonding MO occupied with electrons (the alkene's HOMO) as the
py + py –> π MO. This alkene π MO dominates the chemistry of alkenes by inhibiting bond rotation, acting
as an electron rich Lewis base centre, allowing addition reaction to
occur, etc.
- Also important is
the antibonding π*
antibonding MO, the alkene's LUMO.
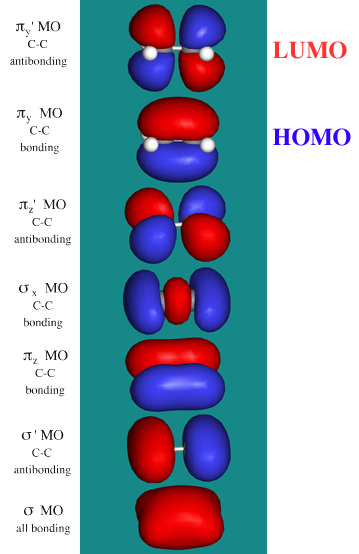
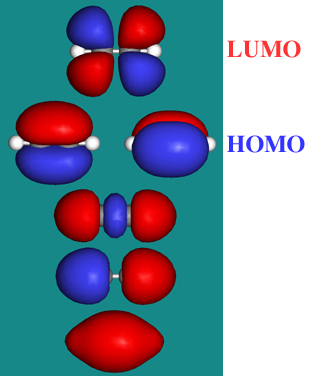
Ethyne (Acetylene)
Ethyne, HC≡CH, has four atoms and 10 valence electrons in four molecular orbitals:
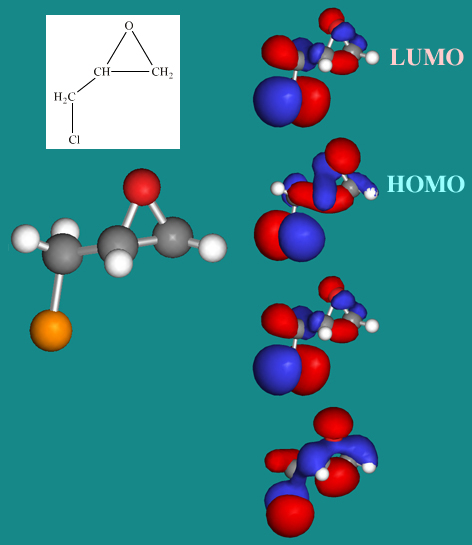
Epichlorohydrin
Epichlorohydrin is an organic molecule of intermediate complexity (and low symmetry). The MOs include:
Arrrrrrrgh... Molecular Orbitals Make My Head Hurt!
Mine too.
Richard Feynman said (here): "I think I can safely say that nobody understands quantum mechanics."
Put another way:
- Electron interactions obey
various selection rules and as a result give rise to involved patterns
with an intrinsic beauty and sometimes extraordinary complexity.
- The electron interaction
patterns can be calculated/predicted/modelled using advanced mathematical
routines running on fast computers.
- However, that that does
not mean that electron interactions – quantum mechanics –
can be fully known and understood in an intellectual sense. Ultimately,
it is just how our world works.
- Actually matters are even more involved than implied above. As discussed elsewhere in the chemogenesis web book wavefunctions are mathematically complex entities, and atomic and molecular orbitals cannot be directly observed in principle.
An analogy from engineering: Finite Element Analysis
Finite element analysis (FEA) is a technique for modeling mechanical structures such as: bridges, cranes and con-rods. A mathematical model of the object is created in a CAD program, which is then subjected to virtual loads. The displacement of the structure – the degree of bending – is determined by treating the object as millions of tiny, interconnected triangles, the finite elements. Overall stress is determined by considering the stresses of each finite element. The results can be presented as stress diagrams:

Image captured from L N Engineering.
Finite elements analysis is conceptually simple, unlike quantum mechanics, but it plays a similar role for the engineer as computational chemistry software does for the chemist.
Engineers can design a con-rod and predict the stresses in the solid, physical item. Likewise, a chemist can design a molecule in a software package like Spartan and predict bond-lengths, bond angles, van der Waals surfaces, conformers, rotormers, etc. with great confidence.
An engineer can zoom in and view each hypothetical finite element, if necessary. Likewise, the chemist can look inside the calculations and visualise the contributing molecular orbitals, should she so wish. There is more on finite element analysis in Wikipedia
Hybridization
Atomic and molecular orbitals are derived from the Schrödingerwave equation, and are actually wavefunctions (waves). Waves are well understood mathematically, and can be added together or subtracted from each other. Consider two sine waves, the product is a superposition, here:
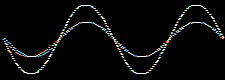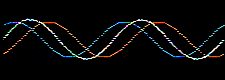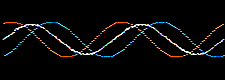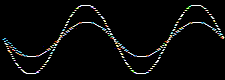
In molecular orbital theory, atomic orbitals on adjacent atoms are added together to give a linear combination of atomic orbitals (the LCAO approximation) which are used to construct molecular orbitals.
However, there is an alternative approach: The s, p and d atomic orbitals can be added together (mixed or hybridized) to produce hybrid atomic orbitals. Then, atoms in various compatible hybridization states can be joined together into polyatomic molecules. Hybridization, part of valance bond (VB) theory, was presented by Linus Pauling in 1930.
Actually, the MO and VB approached are, in principle, exactly equivalent. It is just that the LCAO approximation is very much easier to implement mathematically and it methodology has been extensively developed over the past 80 years.
On the other hand, VB theory and hybrid atomic orbitals are much easier for the human brain to conceptualise and understand.
The s and p atomic orbitals can be added together in various ways:
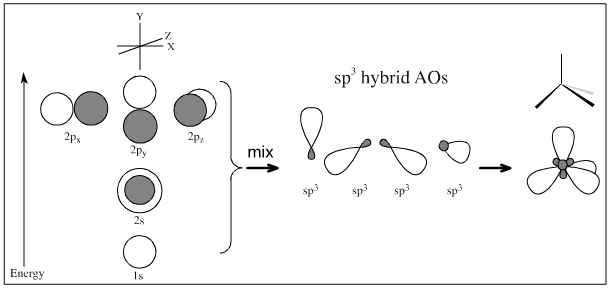
2s + 2p + 2p + 2p → sp3 + sp3 + sp3 + sp3 => sp3 hybridised centre
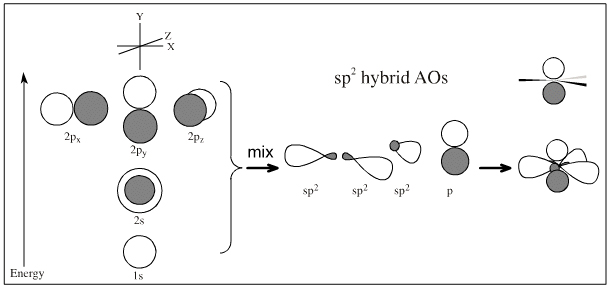
2s + 2p + 2p + 2p → sp2 + sp2 + sp2 + p => sp2 hybridised centre
2s + 2p + 2p + 2p → sp + sp + p + p => sp hybridised centre
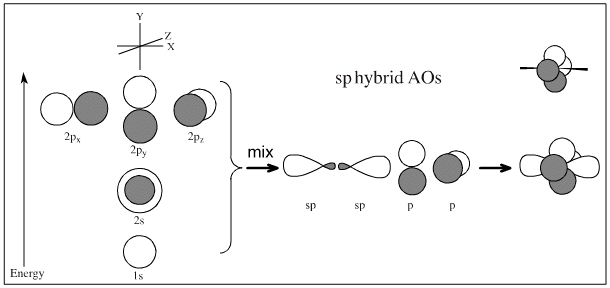
sp3, sp2 and sp hybridisation can be associated with carbon, nitrogen, oxygen atomic centres with various charge states. (Only these atoms are discussed here, there are many types of hybridisation.)
- The various centres can be associated with well known functional groups, reactive intermediates and fragments.
- They can be associated with equivalent VSEPR centres, even though these are constructed in an entirely different way, not involving waves.
|
Atomic
Centre |
Function
|
Formula
|
Hybridisation
State |
Hybridisation
Diagram |
VSEPR
Centre |
VSEPR
Diagram |
|
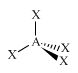
C
|
Alkane
|
CH4
|
sp3
|
 |
Tetrahedral
AX4 |
 |
|
C–
|
Carbanion
|
H3C–
|
sp3
|
 |
Trigonal
pyramidal AX3E |
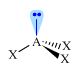 |
|
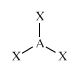
C
|
Alkene
(part of) |
H2C=
|
sp2
|
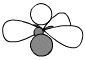 |
Trigonal
planar AX3 |
 |
|
C+
|
Carbenium
ion
|
H3C+
|
sp2
|
 |
Trigonal
planar AX3 |
 |
|
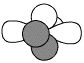
C
|
Alkyne
(part of) |
HC≡
|
sp
|
 |
Linear
AX2 |
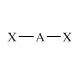 |
|
N
|
Amine
|
NH3
|
sp3
|
 |
Trigonal |
 |
|
N+
|
Ammonium
ion
|
[NH4]+
|
sp3
|
 |
Tetrahedral
AX4 |
 |
|
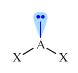
N
|
Imine
(part of) |
HN=
|
sp2
|
 |
Angular
AX2E |
 |
|
N
|
Nitrile
(part of) |
N≡
|
sp
|
 |
Terminal
|
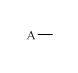 |
|
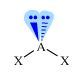
O
|
Water
|
H2O
|
sp3
|
 |
Angular
AX2E2 |
 |
|
O+
|
Oxonium
ion
|
[H3O]+
|
sp3
|
 |
Trigonal
pyramidal AX3E |
 |
|
O
|
Carbonyl
(part of) |
O=
|
sp2
|
 |
Terminal
|
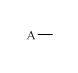 |
|
O+
|
Acyl
cation
(part of) |
+O≡
|
sp
|
 |
Terminal
|
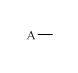 |
The various hybridised atomic centres can be "plugged together" to produce larger polyatomic structures. The rule is that like-joins-with-like:
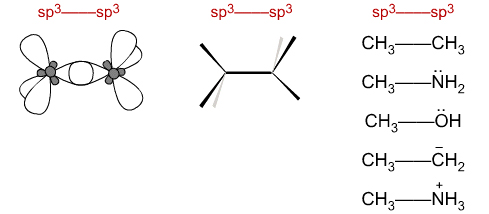
sp3 + sp3 centres plug together to give structures like: CH3CH3, CH3NH2, CH3OH, CH3CH2– and CH3NH3+.
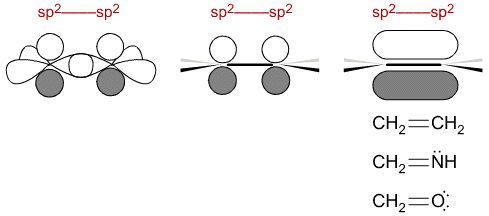
sp2 + sp2 centres plug together to give structures like: CH2=CH2, CH2=NH and CH2=O. Notice that the p-orbitals overlap to produce a π-molecular orbital, often called a π-bond or even just a 'double bond'.
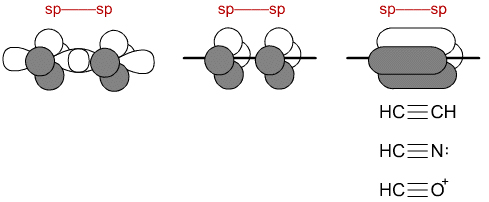
sp + sp centres plug together to give structures like acetylene (ethyne) and hydrogen cyanide. Notice that the two p-orbitals overlap to produce two π-molecular orbitals, often called a 'triple bond'.
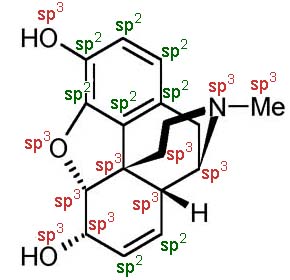
A molecule like morphine is constructed form hydrogen, carbon, nitrogen and oxygen with the C, O & N atoms in sp3, sp2 and sp states of hybridization:
The VB/VSEPR atomic centres are available as plastic plug-together-atomic-centres in numerous molecular model kits:

Understanding Molecular Structure: A Smörgåsbord of Theories
In this author's opinion it is usually too difficult to understand the molecular orbital structure of low symmetry multi-atom species like epichlorohydrin. We have computers to run sophisticated software that can keep track of the multiple arrays of complex numbers and calculate energies and equilibrium geometries.
Chemists mix & match theories and make conceptual simplifications when constructing models of molecules.
Polyatomic organic molecules are constructed by plugging sp3, sp2 and sp hybridized centres together. This is literally true when building plastic models of molecules!
The functional group approach, discussed on the next page of this chemogenesis web book, considers large organic molecules as consisting of functional groups (FGs): esters, aldehydes, ketones, carboxylic acids, aromatic rings, etc. When separated by –CH2– (methylene) groups each FG is deemed to behave as a discrete entity.
The Hückel approximation of sigma-pi separability, or σ-π separability, assumes that (as π electrons are at a much higher energy than the σ-skeleton electrons) the σ and π electrons have no influence upon each other. The σ skeleton of an organic molecule is described using hybridized-VSEPR atoms with the Hückel π-system functional groups superimposed 'on top'.
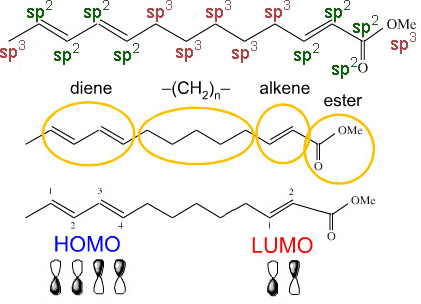
Frontier molecular orbital (FMO) theory models the π-system functional groups. For example, the triene ester, below has a diene HOMO and an alkene LUMO that are able to undergo Diels-Alder cycloaddition to give a bicyclic structure (more here):
 |
 |
 |
| Diatomics | Organic π-Systems & Functional Groups |
© Mark R. Leach 1999 –
Queries, Suggestions, Bugs, Errors, Typos...
If you have any:
Queries
Comments
Suggestions
Suggestions for links
Bug, typo or grammatical error reports about this page,please contact Mark R. Leach, the author, using mark@meta-synthesis.com
This free, open access web book is an ongoing project and your input is appreciated.