Periodic Table |
 |
 |
 |
 |
 |
 |
 |
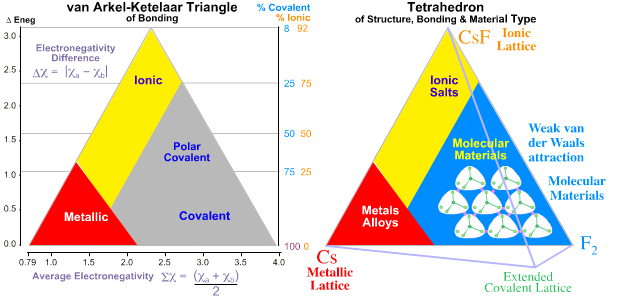
| van Arkel-Ketelaar Triangles | Binary Material Synthlet |
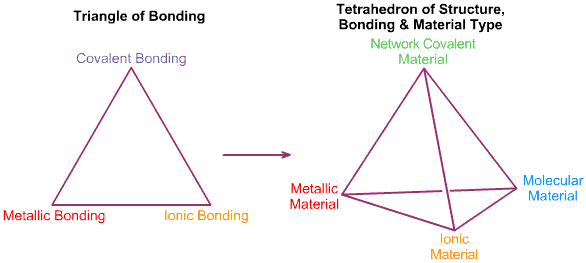
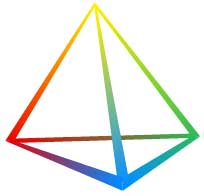
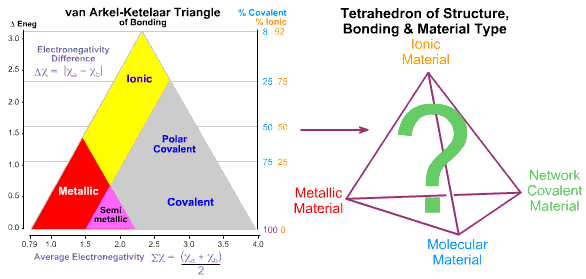
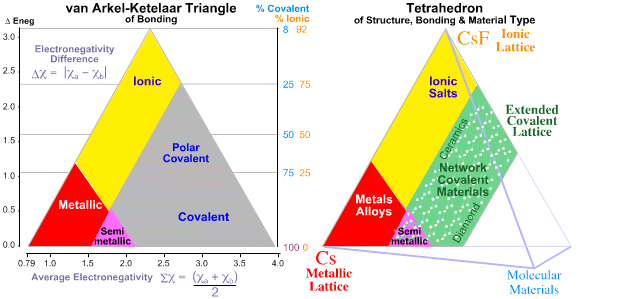
Tetrahedra of Structure, Bonding & Material Type
The van
Arkel-Ketelaar triangle, as discussed on the previous page of this web book, recognises that the chemical elements & binary compounds exhibit three
extreme types of bonding: Metallic, Ionic & Covalent.
But this can not the whole story because covalently bonded materials are seen to
take two extreme forms. They either have an extended three-dimensional covalent network-lattice structure, as exemplified by diamond (carbon) and silicon dioxide (sand), SiO2, and silicon, Si. Or they present as discrete molecules like fluorine, F2, methane, CH4, or glucose, C6H12O6 that interact with each other via weak (van der Waals/dipole-dipole/hydrogen bonding) forces.
This extra dimension leads to a Tetrahedron of Structure, Bonding & Material Type:
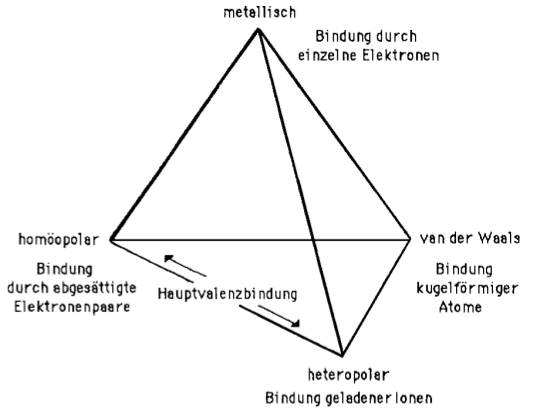
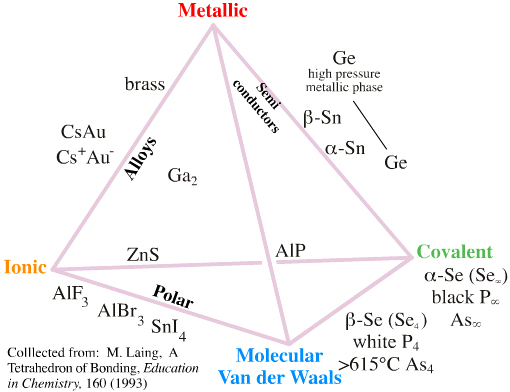
The Grimm Tetrahedron (1928)
William Jensen reports, below, that Grimm and Dehlinger developed an early form of tetrahedron in the nineteen twenties/thirties, however, this knowledge appears to have been forgotten.
The Grimm Tetrahedron symbolically shows the four main types of bonding in solid chemical compounds: metallic (metallisch), ionic (heteropolar), van der Waals (molecular) & network (homopolar).
From William B. Jensen's paper: Logic, History, and the Chemistry Textbook, J.Chem.Educ. 817–828, 75, 1998: Dehlinger's 1934 drawing of Grimm's tetrahedron:
Grimm's two-dimensional projection of his 1934 bond- type tetrahedron redrawn by Jensen using corrected and updated examples:
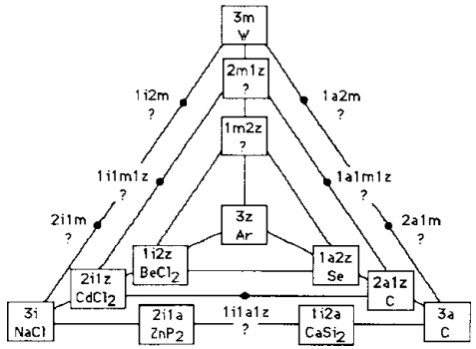
i = Ionenbindung
a = Atombindung
m = metallische Bindung
z = zwischenmolekulare Kräfte
The six edges between these vertices correspond to the intermediate types of bonds. It is clear that the idea of isolated molecules can be most naturally applied only to one vertex of this diagram (the central one, where the intermolecular interactions are the weak van der Waals forces).
This latter representation is employed in the Concept of Chemical Periodicity: from Mendeleev Table to Molecular Hyper-Periodicity Patterns by E. V. Babaev & Ray Hefferlin (1996).
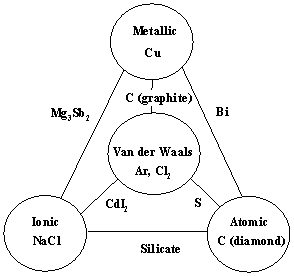
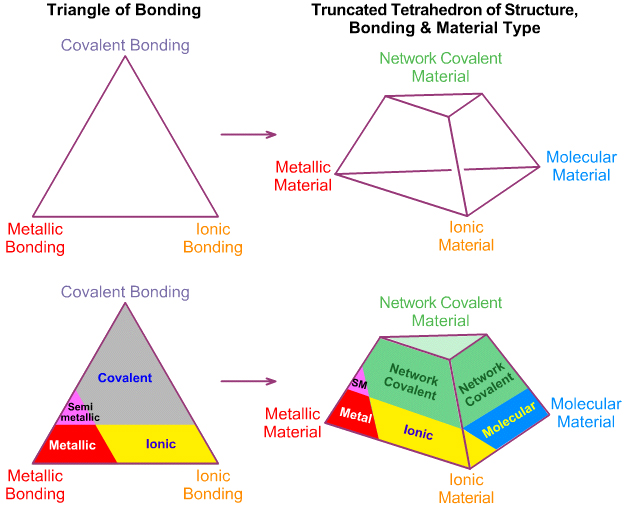
Laing's Tetrahedron of Bonding
In 1993 Michael Laing published an expansion of the two dimensional van Arkel-Ketelaar triangle of bonding into a tetrahedron by dividing covalent materials into two types, Covalent Network and van der Waals Molecular: M. Laing, A Tetrahedron of Bonding, Education in Chemistry, November, pp160-163 (1993):

Representative species:
- Metallic materials:
Copper, Cu, magnesium, Mg, sodium, Na, and chromium, Cr
- Ionic materials:
Sodium fluoride, NaF, magnesium fluoride, MgF2, sodium chloride, NaCl, and calcium oxide, CaO
- Van der Waals
(molecular) materials: Iodine, I2, carbon dioxide, CO2, naphthalene, C10H8, Group 18 (inert)
gases, nitrogen, N2, benzene, C6H6, sulfur hexafluoride, SF6, carbon tetrachloride, CCl4,
and hydrogen bonded solids
- [Network] Covalent materials : Diamond, C, silicon dioxide, SiO2, silicon carbide, SiC
Laing is interested in compounds/materials with intermediate properties. A triangle has three corners and three edges, but a tetrahedron has four corners, four sides and six edges. With respect to the six edges, Laing discusses:
- Van der Waals–to–Metallic: Gallium, Ga2, arsenic and mercury
- Van der Waals–to–Ionic (polar): Aluminium chloride, AlCl3, aluminium bromide, AlBr3, and tin tetraiodide, SnI4
- Ionic–to–Covalent: Zinc sulfide, ZnS, and zinc selenide, ZnSe
- Metallic–to–Covalent (semiconductors): Tin and germanium
- Ionic–to–Metallic (alloys): Copper-zinc brass and cesium-gold alloy
- Covalent–to–Van der Waals: Sulfur, selenium, phosphorus and arsenic
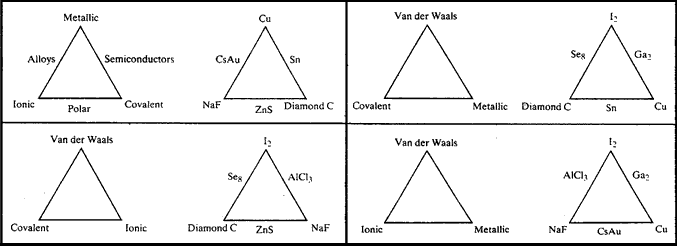
Mike Laing sent (personal communication, 2010) an updated version of his triangle/tetrahedron of bonding:
A Letter from William Jensen
I contacted William Jensen in 2004 for his comments about the earlier version of this page and the Arkel-Ketelaar triangle page, here. Bill very kindly sent me the following email, which I reproduce verbatim:
Mark, "A few historical corrections. Since writing the 1995 article I have discovered that the first bond-type triangle was actually given by Fernelius and Robey in 1935 rather than by van Arkel and was, in turn, partially anticipated by an even earlier triangle given by Grimm in 1928. Details are found in references 1 and 4 below. "Laing is not the originator of the tetrahedral diagram and it should not be named after him. All that he said had been said 60 years before by Grimm and Dehlinger, who in fact had developed a more sophisticated form of the tetrahedron. This tetrahedron was used in several materials science textbooks in the 1950s and 1960s. Details may be found in references 3 and 4 below. "The triangle is a bond type diagram, but the tetrahedron is a structure type diagram. It is important to recognized that these two concepts are not identical. Bond type is only one of several parameters which determine overall structure type. The differences between the two types of diagram are discussed in references 3 and 4 below."
Best Regards: Bill Jensen |
A number of changes have been made to the text on this page as a result of Bill Jensen's communication, particularly the point about triangles of bonding but tetrahedra of structure bonding & material type.
The Four General Types of Crystalline Solid
At an early stage in the study of chemistry we learn that there are four general types of crystalline solid and four associated material types: metals, ionic materials like sodium chloride (salts), molecular materials like methane, CH4, and network covalent materials like diamond.
|
|
|
|
 |
|
|
||
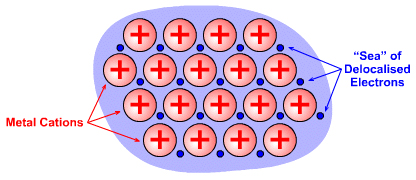
Metallic (Metallisch) Materials
Metals have a characteristic lustre and are excellent conductors of electricity. There are two models of bonding in metals. The classical Drude model of conductivity has a lattice of cations immersed in a sea of mobile valence electrons delocalised over the entire crystal. The positive cations attract the delocalised electrons, and vice versa. The mobile electrons are the agents responsible for the conduction of electricity and heat:
Metals can also be modeled using band theory.
A metal's thermal and electrical conductivities are proportional, but increasing the temperature increases the thermal conductivity and decreases the electrical conductivity, a behaviour quantified by the Wiedemann-Franz Law, here.
From Wikipedia: "The simple classical Drude model provides a very good explanation of DC and AC conductivity, the Hall effect, and thermal conductivity (due to electrons) in metals. The model also explains the Wiedemann-Franz law of 1853. However, the Drude model greatly overestimates the electronic heat capacities of metals. In reality, metals and insulators have roughly the same heat capacity at room temperature. Although the Drude model can be applied to positive (hole) charge carriers, as demonstrated by the Hall effect, it does not predict their existence. |
Metals are often ductile and exhibit a huge range of melting points, from mercury, –39°C, to tungsten at 3200°C. Read more in Wikipedia.
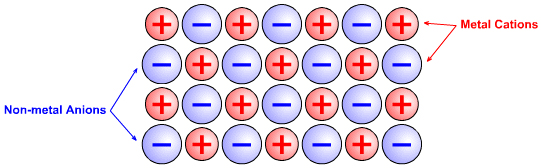
Ionic (Heteropolar) Materials
Ionic materials, such as sodium chloride, NaCl, have an extended crystal lattice with non-metal anions electrostatically attracted to adjacent metal cations and metal cations electrostatically attracted to adjacent non-metal anions:

Ionic materials are insulators as solids, but are electrical conductors when molten and when dissolved in aqueous solution. Ionic materials may dissolve in water (and sometimes in dipolar aprotic solvents such as DMSO), but they are insoluble in non-polar solvents like hexane or chloroform.
Ionic binary materials have moderately high melting points, usually in the 300–1000°C range. Read more about ionic bonding in Wikipedia.
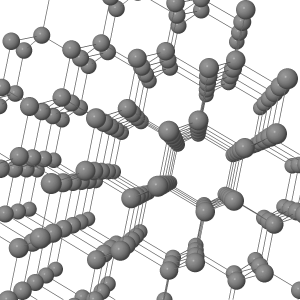
Network Covalent (Homöopolar) Materials
Network covalent materials, such as diamond, C, silicon, Si, and silicon dioxide (quartz and sand), SiO2, have atoms arranged in an extended 3-dimensional lattice of strong, shared electron pair covalent bonds:
Network covalent materials are hard, refractory, brittle, usually electrical insulators, and they are not soluble in any solvent. Materials have very high melting points, >1500°C, and are chemically intractable materials.
Semiconductors are a sub-set of network covalent materials that conduct electricity, albeit with high resistance when pure. The electrical conductivity, modeled using band theory, can be modified by doping, and this is the basis of the transistor and silicon chip – integrated circuit – technology. Semiconductor elements and binary materials include: silicon, gallium arsinide & indium phosphide.
Several elements have pairs of allotropes, one of which is molecular and insulating, and the other which is metalloid: hard, brittle, with a network covalent structure, a metallic lustre and electrical conductivity. These include: carbon (C60 & graphite), tin (gray & white) & arsenic (yellow & grey).
Molecular (van der Waals) Materials
Discrete molecules, such as methane, CH4, and glucose, C6H12O6, are held together internally by strong intramolecular (within molecule) shared electron pair covalent bonds, but when forming condensed solid or liquid phases, the molecules interact/bond with each other via weak intermolecular (between molecule) van der Waals forces and/or hydrogen bonds:
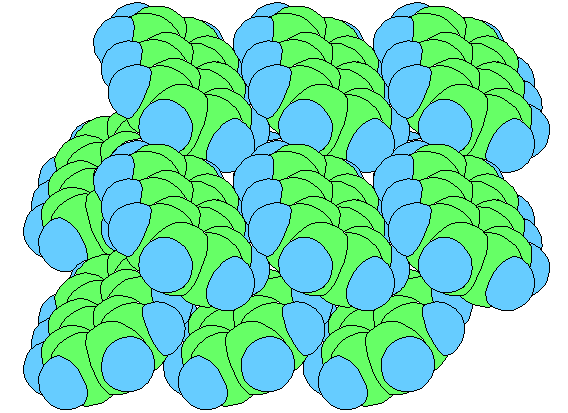
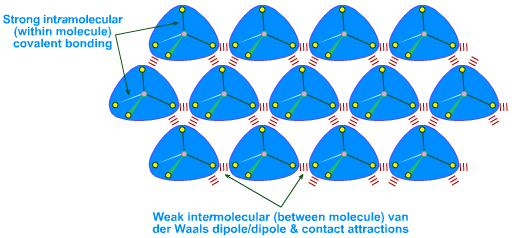
There are several types of van der Waals attraction:
- dipole/dipole attraction
- dipole/induced-dipole attraction
- spontaneous-dipole/induced-dipole attraction
It is tempting to consider these forces to be of different strengths, but it is the distance range that is more important.
The spontaneous-dipole/induced-dipole attractions – also known as London dispersion forces (LDF) – are surprisingly strong but only act at very short range. These are contact attractions: the surface of even neutral, non-polar molecules like methane are 'sticky'.
All molecules have London dispersion forces and the strength increases with the size/surface area of the molecule. This logic is used to explains the increasing boiling and sublimation temperatures of the halogens:
F2 < Cl2 < Br2 < I2
In addition, some molecules have dipole-dipole, hydrogen bonding, etc., which increase the total amount of interaction between the molecules.
A nice example:
Consider iodine chloride, ICl and bromine, Br2. Both are 70-electron systems, but ICl is polar and Br2 is non-polar, yet they have rather similar boiling points of 97° and 59° respectively. Both molecules show induced dipole (London) attraction, but only ICl shows dipole/dipole attraction. The boiling point numbers that the dipole/dipole attraction makes only a rather minor contribution. (Many thanks to members of the ChemEd list for the above points.)
Molecular materials may also be hydrogen bonded, where a hydrogen bond involves a proton being shared between two Lewis bases, usually with oxygen, nitrogen or fluorine atomic centres, as discussed here.
Molecular materials exhibit a vast array of properties, but they are generally mechanically weak, have zero electrical conductivity, have low melting and boiling points, and/or a susceptibility to sublime. Molecular materials usually soluble in (or miscible with) non-polar solvents.
Hydrogen bonded molecular solids are often soluble in water.
Some Points for Consideration:
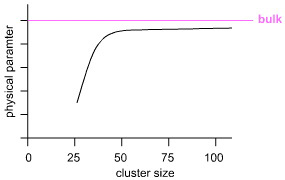
Structural Models & Lattice SizeDiscrete molecules, ie molecular van der Waals materials, are rather easy to model using plastic models and/or computer software because molecular materials are, by definition, of limited size and only consist of a few atoms. Lattice materials – metals, ionic salts & network covalent compounds – are considered to be of infinite size and without surfaces, this is computationally a more difficult task. Indeed, experiment shows that small clusters consisting of hundreds of atoms are required before bulk properties are approached, below. Indeed, if one wishes to calculate/model a bulk property of a molecular material, such as boiling point, it is necessary to consider a lattice of molecular entities. Network covalent materials must, of course, have a surface. The surface does not consist of 'dangling bonds', but can either be oxidised or the surface layer(s) of atoms can rearrange to give a very subtle surface structure.
_surface.png) |
CrystalsThis web page is concerned with bonding and material type, not with crystal type. The science of how atoms, ions and molecules fit together to produce various types of crystallographic unit cell can be explored via Wikipedia. Bob Hanson of St. Olaf College has developed the Jmol Crystal Symmetry Explorer, a web based tool that allows the visualisation of crystal structures. (Note: Your computer must be allowed to run downloaded java applications use this page. Your network administrator may not allow this.) 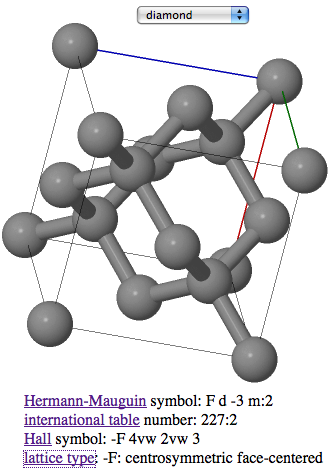
Read more in Stephen Lower's Chem1 Virtual Textbook: States of Matter & Solids. |
SchemasThe van Arkel-Ketelaar triangle and the Tetrahedron of structure, bonding & material type are – like the periodic table – visual schemas that map chemical properties to theories of chemical structure. Like all schemas, anyone is free to have a go at choosing representative species and extending/expanding the property sets. There is still a great deal to discover about the tetrahedron of structure, bonding and material type, and some of this author's ideas – found by standing on the shoulders of Jensen & Laing – follow. |
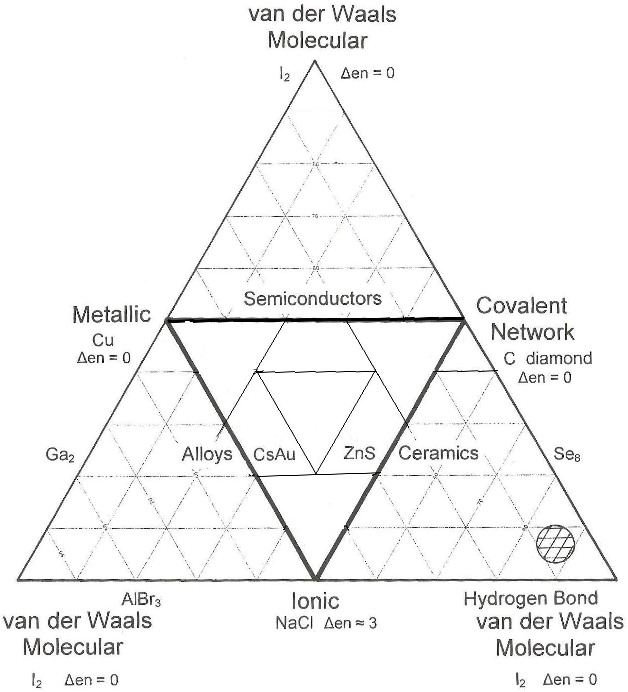
The Quantitative Truncated Tetrahedron of Structure, Bonding & Material Type
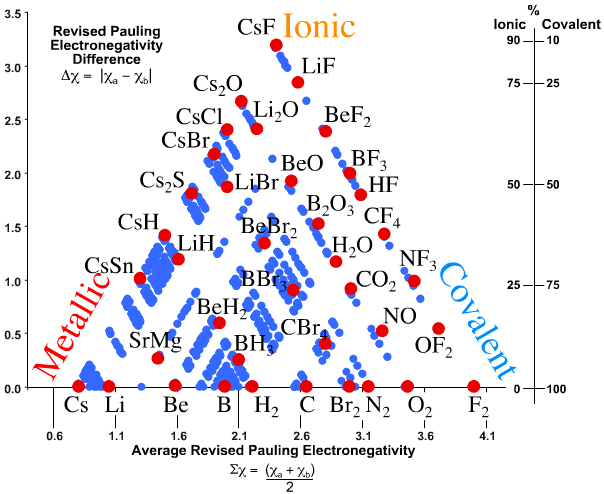
Jensen showed that it is possible to quantify the van Arkel-Ketelaar Triangle of Bonding by looking at average electronegativity and electronegativity difference:
A Quantitative can Arkel Diagram, J.Chem.Educ., 395-398, 72 (1995):
The question is: Can the Tetrahedron of Structure, Bonding and Material Type be Quantified?
A simple valency rule can be used to predict with good – but admittedly not perfect – accuracy whether a binary compound with covalent bonding will be a molecular or network covalent material.
Valency Rule:
- If both of the elements have a common (lower) valency of two or greater and the bonding be covalent the binary compound will likely be a network covalent material: mechanically hard, brittle solid with a high melting temperature that will be insoluble in any solvent.
- Otherwise, if one or both of the atoms has a common (lower) valency of one: H, Li, Na, K, F, Cl, Br or I, and the bonding be covalent, the binary compound will be molecular material that will be mechanically soft, have a low melting temp (and may even be a liquid or gas) and will be likely to be soluble in either polar or non-polar solvents, but probably not both.
- CAUTION! This over simple rule does throw up some important errors: CO2, O2 and N2 are predicted to be network covalent materials and therefore solids... where as they are actually molecular gases.
1 + 1 |
Molecular: Ionic: |
H2, HCl, Cl2, LiH(gas) LiH(solid), NaCl |
1 + 2 |
Molecular: Ionic: |
H2O, OF2, SCl2 MgF2, Na2O |
1 + 3 |
Molecular: |
NH3, PCl3, BF3 |
1 + 4 |
Molecular: |
CH4, SiCl4 |
1 + 5 |
Molecular: |
PCl5, IF5 |
2 + 2 |
Molecular: Chain: Ionic: |
O2, S8 (-S-S-S-S-S-S-)n MgO, CaS |
2 + 3 |
Network: |
aluminium oxide, Al2O3 |
2 + 4 |
Network: Special case molecular: |
silicon dioxide, SiO2 carbon dioxide, CO2, however, at high pressure carbon dioxide is now known to form an extended network structure |
3 + 3 & 3 + 5 |
Network: Special case molecular: |
aluminium phosphide, AlP, boron nitride, BN, gallium arsinide, GaAs nitrogen, N2, white phosphorous, P4 |
3 + 4 |
Network: |
silicon nitride, Si3N4 |
4 + 4 |
Network: Special case clusters: |
silicon carbide, SiC carbon, C60, etc. |
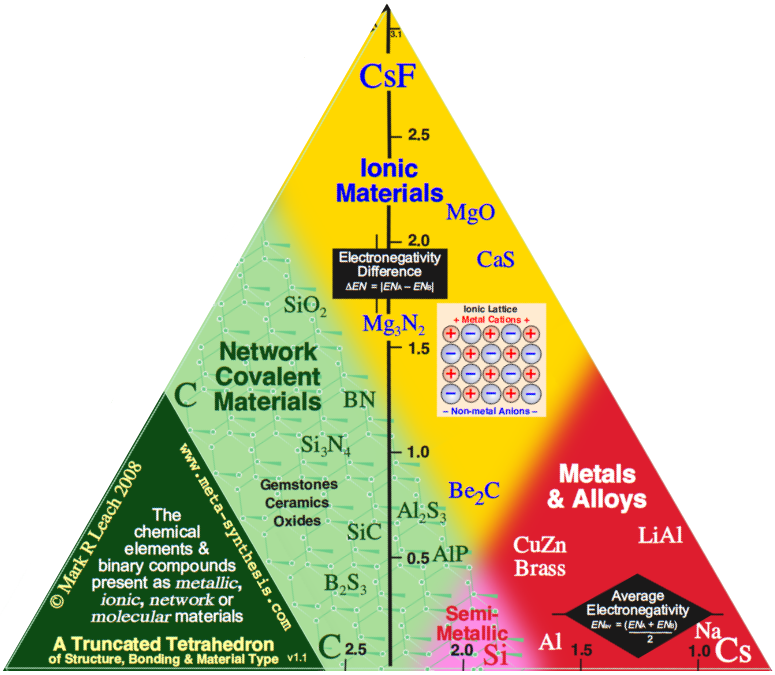
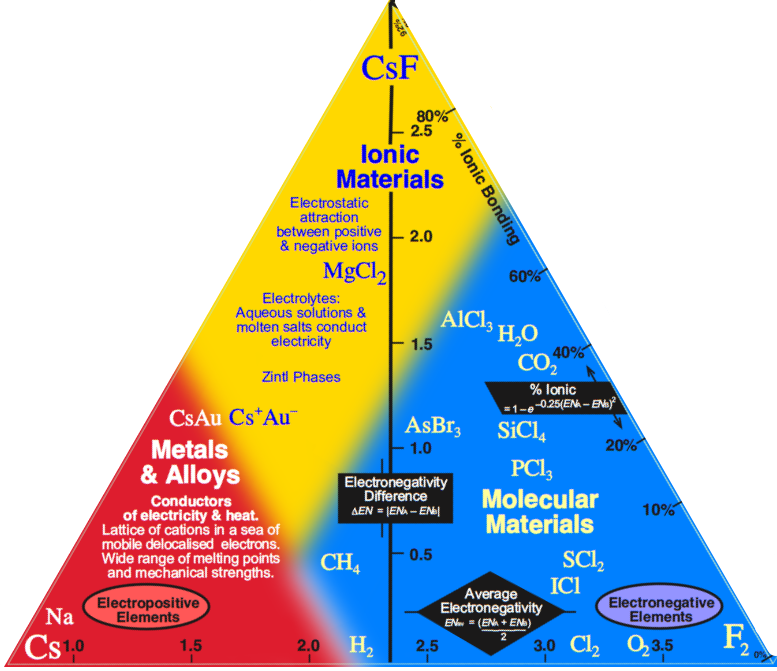
Observation: Three of the corners of the quantitative tetrahedron are clear: Cs, F2 and CsF.
- Metallic: Cesium, Cs, is a metal and the most electropositive element, 0.79.
- Molecular: Fluorine is the most electronegative element, 3.98, it is molecular, F2, and the covalent bond is non-polar.
- Ionic: Cesium fluoride, CsF, is the most ionic binary compound, 3.98 – 0.79 = 3.19.
But what about the fourth corner, Network Covalent?
- The most electronegative element that forms a network covalent material is carbon, 2.55.
It follows that diamond should not be placed at the corner of a tetrahedron at electronegativity 3.98, but at some distance from it, at 2.55.
Indeed, the corner of the tetrahedron should be cut off at 2.55, giving a truncated tetrahedron.
A Physical Semi-Quantitiative Truncated Tetrahedron
Click to download truncated_tetrahedron.pdf, print, cut out, score & glue together:
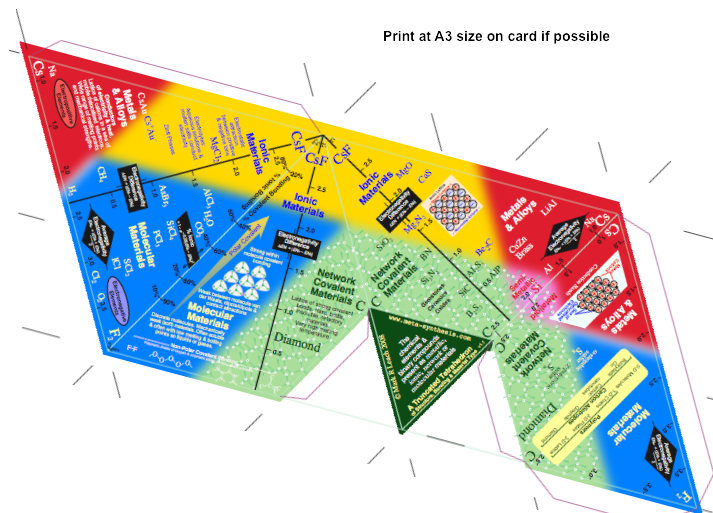

The meta-synthesis Semi-Quantitiative Truncated Tetrahedron of Structure, Bonding & Material Type: The Four Faces
The molecular to network edge, with the text "Non-Polar Covalent Bonding" (above) should have the species:
- F2 molecular fluorine
- [-OO-]n polymer chains of oxygen atoms
- [N]n 2D polymeric nitrogen (flat plates like graphite)
- [C]n 3D polymeric carbon, diamond
Unfortunately, the polymeric oxygen and nitrogen allotropes are unknown!
Structural Theory and the Truncated Tetrahedron
Models & theories of chemical structure & bonding can be mapped onto the Truncated Tetrahedron of Structure, Bonding & Material Type.
The theoretical models for metals and semiconductors use band theory, ionic materials use lattice models, molecular and network materials are modeled either by molecular orbital (MO) theory or by valence shell electron pair repulsion (VSEPR):
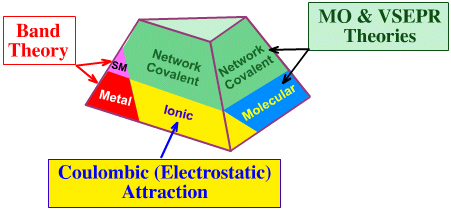
Band Theory: Metals, Alloys & Metalloids (Semi-metals)
When metal atoms collect together to form metal, the atomic orbitals overlap form molecular orbitals which range from completely bonding to completely antibonding. These MOs can be separated into conducting and non-conducting bands with as many energy levels as there are electrons. If a material has electrons in the conduction band it will conduct electricity and heat, if there are no electrons in the conducting band it will be an insulator. Semiconductors have a few electrons in the conduction band. Read more in the Wikipedia.Coulombic (Electrostatic) Attraction: Ionic Materials
It is convenient to think of ionic solids as consisting of a lattice of idealised spheres of definite size and charge, subject only to Coulombic (electrostatic) attraction. Positive cations are attracted to adjacent negative anions, and vice versa. In the simplest models electrons are not shared.The structure of many ionic materials can be accounted for in terms of the relative sizes of the ions, their relative numbers, the radius ratios, and their preference for tetrahedral or octahedral coordination. Crystal structure can usually be explained in terms of Pauling's Five rules:
- Around every cation, a coordination polyhedron of anions forms, in which the cation-anion distance is determined by the radius sums and the coordination number is determined by the radius ratio.
- The Electrostatic Valence Rule: An ionic structure will be stable to the extent that the sum of the strengths of the electrostatic bonds that reach an anion equals the charge on that anion.
- The sharing of edges, and particularly faces by two anion polyhedra decreases the stability of a crystal.
- An extension of the third rule: In a crystal which contains different cations, those with high charge and low coordination numbers tend not to share elements of their coordination polyhedra.
- The Rule of Parsimony The number of essentially different kinds of constituents in a crystal tends to be small.
Crystal structures are usually named after a definitive crystal structure, such as: zinc sulfide (structure), sodium chloride, cesium chloride, calcium fluoride (fluorite), rutile, diamond, etc.
MO Theory & VSEPR: Molecular and Extended Lattice Structures
Molecular and network covalent materials can be modeled in terms of hybridized atomic centres and/or valence shell electron pair repulsion (VSEPR) entities. For example, sp3, tetrahedral carbon is found in molecular methane, CH4, and in the extended network covalent of diamond. Molecular structures can be modeled in more detail with (paramertised) molecular mechanics software or with molecular orbital theory.
A more detailed discussion of structural theory is available elsewhere in the Chemogenesis web book, here.
Six Edges To The Tetrahedron
There are six edges to the Tetrahedron of Structure, Bonding & Material Type and the trends associated with each edge will be discussed in turn:
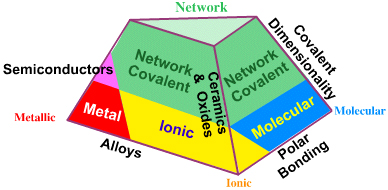
- Molecular – Network: Molecular Covalent Dimensionality
- Ionic–Network: Ceramics & Oxides
- Metallic–Molecular (not shown on diagram): Cluster Compounds
- Metallic–Ionic: Alloys
- Ionic–Molecular: Polar Bonding
- Metallic–Network: Semiconductors
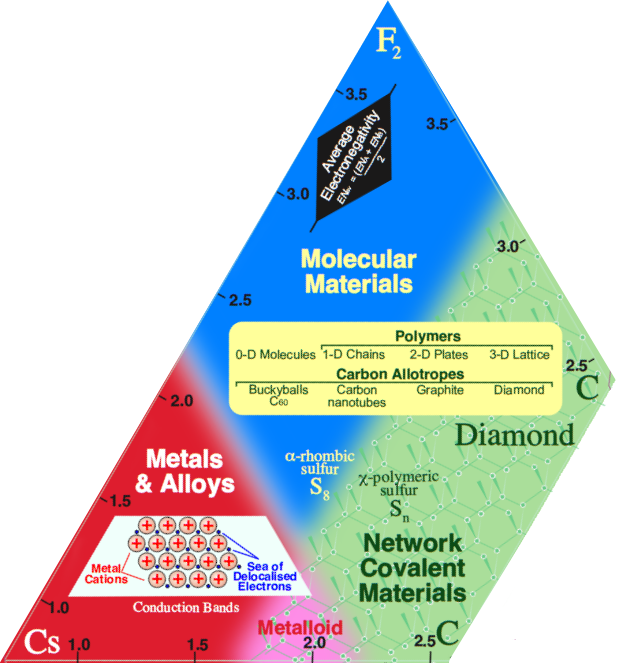
Molecular – Network: Molecular Covalent Dimensionality
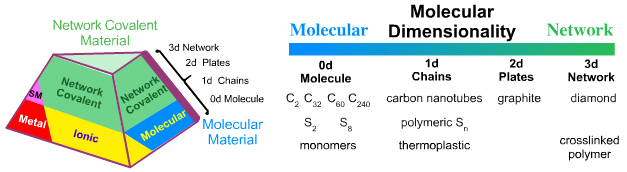
If an extended network covalent structure is three dimensional, 3d, and plates are two dimensional, 2d, then chains are one dimensional, 1d, and discrete molecules are zero dimensional, 0d, with respect to extended structure, ie at the millimeter scale.
The molecular to network edge should have the species:
- F2 molecular fluorine
- [-OO-]n polymer chains of oxygen atoms
- [N]n 2D polymeric nitrogen (flat plates like graphite)
- [C]n 3D polymeric carbon, diamond
Unfortunately, the polymeric oxygen and nitrogen allotropes are not known.
Carbon allotropes beautifully illustrate covalent molecular dimensionality:
- Diamond has a three dimensional, 3d, network covalent structure
- Graphite consists of two dimensional, 2d, covalent plates
- Single wall carbon nanotubes are one dimensional, 1d, tubes
- C60 buckyballs are zero dimensional, 0d, molecules. C2 is known in the gas phase at high temperature. On the millimeter scale these are point entities.
- Read a series of reviews about carbon chemistry in Materials Today.
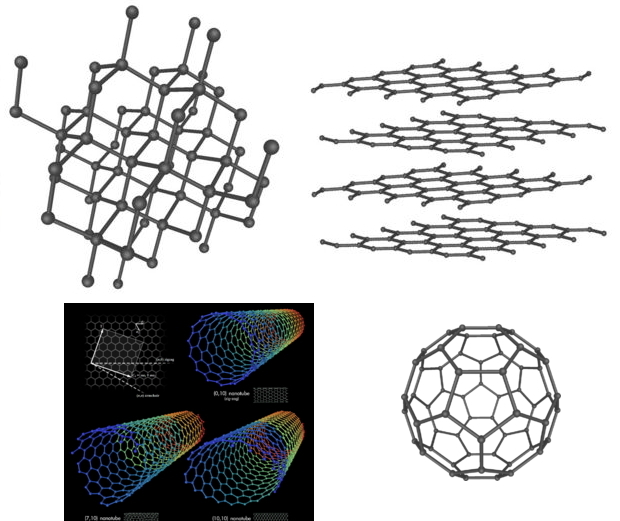
Composite image of three dimensional diamond, two dimensional graphite, one dimensional carbon nanotubes and zero dimensional – with respect to extended structure– C60. From Wikipedia: here, here & here
Sulfur has zero dimensional and one dimensional allotropes.
- Above 600°C sulfur exists as S2, a species isoelectronic with O2.
- At 20°C sulfur exists as the yellow crystalline allotrope Flowers of Sulfur (Brimstone) which consist of S8 rings.
- Clever chemistry can be used to make ring sizes of 6, 7, 9, 10, 11, 12, 18 & 20.
- Heating to 160°C causes the S8 rings to open and polymerise. Rapid cooling traps this 1d polymeric state... which slowly turns back into the flowers of sulfur allotrope at room temperature over several days.
Polymer chemistry involves converting small monomers, such as ethylene (zero dimensional entities) into one dimensional thermoplastic chains such as low density polyethylene (LDPE), or three dimensionally crosslinked (network covalent) materials like urea-formaldehyde resins.
Two further points:
- Between the integer 0d, 1d, 2d and 3d dimensions, there are fractional and fractal dimensions. Take a look at the fractal dimension calculator. There is a 1995 book Fractals in Chemistry.
- Network materials can be ground to fine powders, or synthesized as nano-sized particles. This important because size will strongly influence physical and chemical properties.
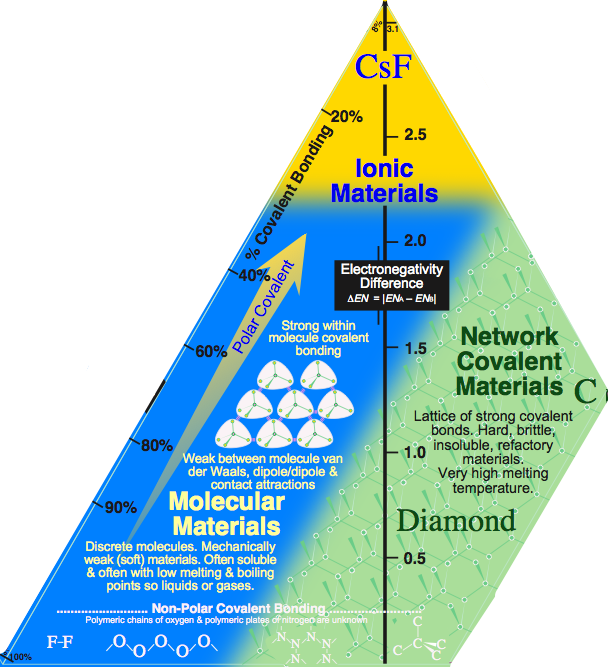
Ionic–Molecular: Polar Bonding
Like many authors, Laing identifies aluminium chloride, AlCl3, as intermediate between ionic and molecular because aluminium chloride sublimes (as Al2Cl6) so is molecular, but the intramolecular Al-Cl bonds are highly polarised. The difference in electronegativity can be used to calculate the % ionic and % covalent character using the Pauling equation, here.
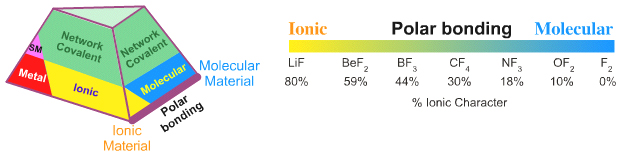
The Ionic-to-Molecular transition is well illustrated by looking at the fluoride, chloride & bromide (halogen) compounds across their periods:
|
LiF
|
BeF2
|
BF3
|
CF4
|
NF3
|
OF2
|
F2
|
|
NaCl
|
MgCl2
|
AlCl3
|
SiCl4
|
PCl3/PCl5
|
SCl2
|
Cl2
|
|
KBr
|
CaBr2
|
GaBr3
|
GeBr4
|
AsBr3
|
SeBr2
|
Br2
|
|
Ionic
|
Molecular, polar covalent
|
Covalent
|
||||
Reading from left to right:
- Ionic materials, ionic bonding, extended crystal lattice
- Molecular materials with polar covalent bonding
- Molecular materials with non-polar covalent bonding
There is a material type discontinuity going from a molecular van der Waals material to an ionic material. For example, on heating MgCl2 and AlCl3:
- Magnesium chloride, MgCl2, melts to give an ionic liquid that conducts electricity.
- Aluminium chloride, AlCl3, sublimes to give a gas of dimeric Al2Cl6 then AlCl3 molecular entities.
Ionic and polar materials can be ground to fine powders, or synthesized as nano-sized particles that approach molecular sizes.
Ionic–Network: Polar Ceramics and Oxides
Laing identifies zinc sulfide and zinc selenide, ZnS & ZnSe, as intermediate between ionic and network covalent. While there in nothing wrong with this analysis, it limited because a whole range of commercially important materials are to be found.

To consider polar ceramics and oxides it is necessary to identify which part of the tetrahedron we are discussing. For this topic we are not just to looking at Ionic-Network "edge", but the entire Ionic-Network-Molecular face.
Oxides range: Ionic <-> Polar Network <-> (Non-polar Network)
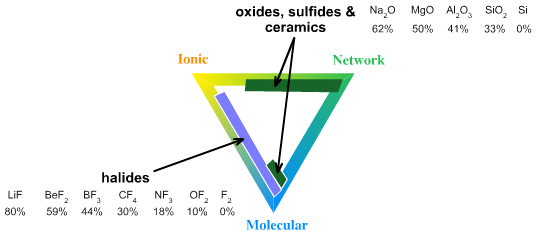
Ceramics are forming an ever more important part of our lives, but often in unexpected places. In the 1970s there was much talk in the engineering research community about building ceramic internal combustion engines, but the ceramics proved too difficult to work with and the topic is hardly discussed today. However, ceramics are now widely used in modern high performance engines, but they are employed as thin films and coatings rather than as parts.
- Engines used to be made of low quality cast iron with the pistons running in iron liners.
- In the 1970s aluminium engines were developed, but they retained their hard wearing iron liners. However, there were problems with the differential thermal expansion of the aluminium engine block and the iron liners that limited performance.
- Today, high performance engines are all aluminium alloy, with the cylinder bore (and possibly the piston rings) evenly coated with a few microns of a ceramic material such as silicon carbide or titanium nitride. (Different companies have their own proprietary recipes, for example CKS, a patent coating from Goetze.)
Planets, including the Earth, are made from rocks & minerals.
- Minerals are characterised by having a distinct crystal structure, and there can be exchange between cations, and exchange between anions so that a particular mineral can have a range of compositions. For example, the mineral rhodonite: manganese iron magnesium calcium silicate (Mn, Fe, Mg, Ca)5(SiO3)5 can vary in the exact ratio of Mn, Fe, Mg & Ca cations, as long as the net charge adds to 10, so as to counter the 5 silicate ions, [SiO3]2-.
- Most of the minerals that make up the earth's crust are oxides of silicon, aluminium & iron which give rise to polar network covalent materials which are: high melting point, insulating, insoluble materials.
- Most rocks – when examined closely – are found be assemblage of two or more minerals.
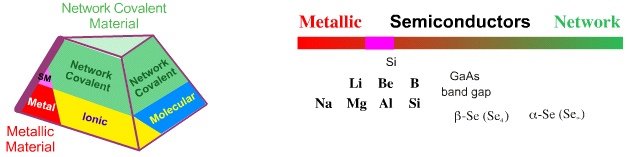
Metallic–Network: Semiconductors
Laing suggests that tin, Sn, is the ideal intermediate between metallic and network, because Sn has two allotropes, metallic β-tin and network covalent α-tin, and supports this suggestion with the story of how Napoleon's army had uniform buttons made from metallic tin, but during the attempted to invasion of Russia in 1812, the intense cold of winter transformed the metallic tin buttons into the mechanically weak network covalent allotrope of tin... and to powder...
There is a discontinuity in bonding – from metallic to covalent – when crossing a period:
Li |
Be |
B |
C |
N2 |
O2 |
F2 |
Ne |
Na |
Mg |
Al |
Si |
P4 |
S8 |
Cl2 |
Ar |
K |
Ca |
Ga |
Ge |
As |
Se |
Br2 |
Kr |
Metallic |
Covalent Bonding |
||||||
This discontinuity occurs due to the phase change from metallic to network covalent, as illustrated by the alpha and beta allotropes of tin. This phase change is independent of the onset of conductivity as described by band theory. Silicon has an extended network covalent structure: it is hard, brittle, has a high melting point, 1420°C, and is insoluble. However, Si also conducts electricity (albeit slightly) and has a metallic lustre.
In Periodicity and the s- and p-Block Elements (OCP 51, 1977, pp58), N.C. Norman reminds us that the metalloid, or semi-metallic, elements have a narrow range of electronegativity values, 1.8-2.2:
- B (2.04)
- Si (1.9)
- Ge (1.81)
- As (2.18)
- Sb (2.05)
- Te (2.1)
Furthermore, binary materials with average electronegativity values in this range can also be metalloid. Examples include:
| Gallium arsenide |
GaAs
|
(1.81
+ 2.18)/2
|
1.99
|
| Indium antimide |
InSb
|
(1.78
+ 2.05)/2
|
1.91
|
| Silicon carbide |
SiC
|
(1.9
+ 2.55)/2
|
2.22
|
| Aluminium phosphide |
AlP
|
(1.61
+ 2.19)/2
|
1.90
|
| Gallium phosphide |
GaP
|
(1.81
+ 2.19)/2
|
2.00
|
| Indium phosphide |
InP
|
(1.78
+ 2.19)/2
|
1.99
|
Ultra pure silicon is actually a poor conductor but its electronic properties can be dramatically modified by doping with small quantities of "impurity" atoms.
- Substitution of a silicon atom with a phosphorus, arsenic or antimony atom (at the parts per million level) will increase the number of electrons in the conduction band and make the material more conducting. This type of material is classed as an n-doped semiconductor, here.
- Substitution with boron, aluminium or gallium will reduce the number of electrons so that there are "electron holes". Such materials are classed as p-doped semiconductors, here.
- When p-doped semiconductors are joined to n-doped semiconductor so that there is a pn junction, a device is formed which will only allow electricity to flow in one direction. Such a device is called a diode, here.
- Materials like gallium arsenide, GaAs, and indium antimide, InAs, are isoelectronic with silicon and germanium and are known as III/V semiconductors.
- Research is being carried out on the doping of diamond to give it semiconductor properties.
Metallic–Molecular: Cluster Compounds
Laing identifies the digallium molecule, Ga2, as the intermediate between metallic and van der Waals molecular. I argue, as above, that there many intermediates and it is possible to identify and describe the gradual change from metallic to molecular behaviour.
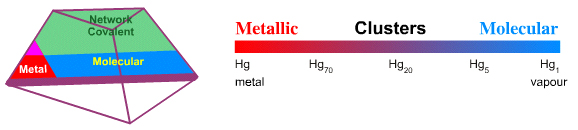
In a News and Views article – Nature, 331, 14th Jan, pp116, 1988 – Tony Stace asks the question:
"How large does a collection of atoms have to be before it begins to adopt the properties and features of a solid?"
The question is answered with reference to metallic clusters.
- It transpires that when the ionisation energy of mercury clusters is measured there is a gradual transition from essentially atomic behaviour for small clusters (5-10 atoms) to metallic behaviour (60-70 atoms). Thus, it seems that for mercury when a couple of dozen or so atoms bond together, there is sufficient atomic orbital overlap for a conduction band to form and for the material to adopt bulk metallic properties.
- Copper clusters only adopt the interatomic distance of bulk copper when the cluster size is greater than 10 atoms.
- The melting point of gold clusters increases with cluster size and more than 1000 atoms are required before the mp of the cluster approaches the mp of bulk gold:
Number of Atoms |
Melting Point °C |
20 |
500 |
50 |
800 |
100 |
920 |
200 |
980 |
bulk
gold |
1064 |
- Non-metals: Small argon clusters (20-50 atoms) exhibit icosahedral (five fold) symmetry. Larger clusters (>100 atoms) and solid argon have a face centred cubic crystalline structure and octahedral symmetry.
A graph of cluster size vs physical parameter (ionisation energy, interatomic distance, melting point) typically takes the following form with a distinct inflection point between molecular and bulk behaviour. The inflection point varies with element and experimental parameter.
Metallic–Ionic: Alloys
Laing discusses the Metallic-Ionic edge with respect to alloys, particularly the various copper-zinc (brass) alloys that have properties very different to the pure metals, and the cesium-gold intermetallic compound, CsAu or Cs+/Au–, which is intermediate between metallic and ionic.

Alloying involves mixing of two or more metals to create an entirely new material, eg. the fusion of copper and tin to make bronze. The mixing is usually carried out by melting a mixture of the solid metals in the desired proportions.
However, like water and organic solvents not all molten metals are fully miscible with each other.
- Copper and nickel are completely soluble in each other. On cooling, the copper and nickel atoms are randomly distributed in the metallic lattice. These are substitutional alloys, examples include: Cu/Ni Cu/Au & Na, K, Rb & Cs in all proportions
- When a small amount of zinc is added to liquid copper it will dissolve and form a substitutional alloy. However, at >30% zinc, a stoichiometric CuZn phase forms.
- Lithium is only miscible with sodium above 380°C. It is immiscible with potassium, rubidium and cesium and it does not form substitutional alloys.
- Lead and copper are immiscible.
- The earth's core is composed of liquid iron. Elements soluble in liquid iron, called siderophiles, are depleted in the earth's crust compared with the meteorites from which the earth was constructed. It is suggested that the siderophile metals partitioned into the iron core very early in the earth's history. Siderophile metals include: iron, nickel, cobalt, platinum, gold, etc., here.
Solid solution alloys form when two metals are totally soluble in both the liquid and solid states.
Eutectic alloys form when two metals are soluble in the liquid state but are insoluble in the solid state. The result, when viewed under a microscope, are grain boundaries in the solid alloy which consists of two distinguishable metals. A typical eutectic alloy is formed with cadmium and bismuth.
Partial solubility alloys are intermediate between solid solution and eutectic.
Intermetallic compounds have a fixed stoichiometric composition. For example, two atoms of magnesium combine with one atom of tin to give Mg2Sn. Likewise, cesium and gold form an intermetallic, CsAu which has properties of Cs+/Au–. The intermetallic iron carbide (Fe3C) or cementite is important in the phase diagram of steel, here. Intermetallic compounds are usually hard, brittle have low conductivity.
Zintl phases,Wikipedia, are valence compounds formed between electropositive metals and main group and post-transition elements. Syntheses are performed in liquid ammonia. Compounds are stoichiometric with salt like structures. In liquid ammonia polyatomic clusters form. Typically, Zintl phases are brittle, coloured and are semiconducting.
|
Metallurgy: Steel as Iron-Carbon Alloy Alloys and alloy science - metallurgy - can be highly involved. Prof. Joe Bellina – an academic physicist at Saint Mary's College, Notre Dame, Indiana, USA – made an interesting contribution to the ChemEd list on the subject of iron and steel alloys which illustrates this point. (Many thanks to Joe for permission to use the following text):
Now consider the skilled blacksmith, who from experience knows:
More
information on carbon steels, including the phase diagram, can
be found here.
|
Binary Material Software Widget: A Semi-Quantitative Tetrahedron
On the next page of this web book there is a Binary Material Software Synthlet that predicts bonding and material type from pairs of main-group elements in a semi-quantitative manner.
It works by determining whether a material is likely to be molecular or network from valency data, and then it projects the van Arkel-Ketelaar on to the appropriate face of the tetrahedron of bonding and material type:
 |
 |
 |
| van Arkel-Ketelaar Triangles | Binary Material Synthlet |
© Mark R. Leach 1999 –
Queries, Suggestions, Bugs, Errors, Typos...
If you have any:
Queries
Comments
Suggestions
Suggestions for links
Bug, typo or grammatical error reports about this page,please contact Mark R. Leach, the author, using mark@meta-synthesis.com
This free, open access web book is an ongoing project and your input is appreciated.