Periodic Table |
 |
 |
 |
 |
 |
 |
 |
| Modern Lewis Theory | Diatomics & MO Theory |
Valence Shell Electron Pair Repulsion
Valence shell electron pair repulsion, VSEPR, is a super-simple technique for predicting the geometry of atomic centres in molecules and molecular ions:
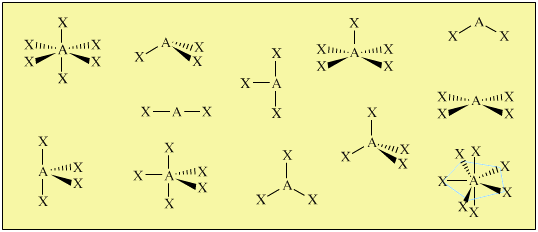
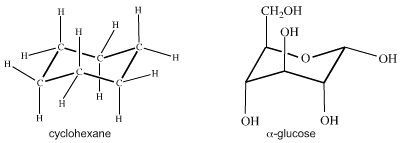
Crucially, atomic centres with VSEPR determined geometry can be joined together into molecular entities like cyclohexane and glucose:
This molecular building-block logic can be extended, enabling large biomolecular structures like DNA to be modelled and structurally understood:

The VSEPR Technique
Six or so steps are required to generate the VSEPR geometry of an atomic centre such as:
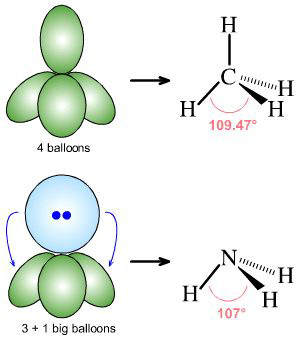
Carbon in methane, CH4
Nitrogen in ammonia, NH3
Xenon in xenon tetrafluoride, XeF4
Iodine in the iodide difluoride ion, [IF2]–
|
First, determine the number of electrons in the outer (valence) shell about the central atom (C, N, Xe, I, etc.): 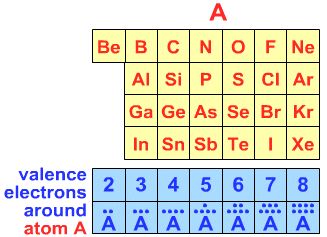
|
|
Second, find valency and number of electrons associated with the ligand X:  |
|
Third, construct a valid Lewis structure of the molecule in question showing all of the bonds and all of the lone pairs (nonbonded pairs) of electrons. If the structure is a molecular ion, add one valence electron for each negative charge and remove one valence electron for each positive charge. 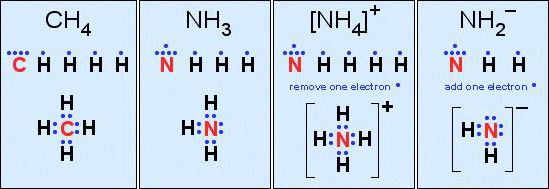
Not all Lewis structures have eight electrons about the central atom A (as emphasized by very simple Lewis octet theory). For example,
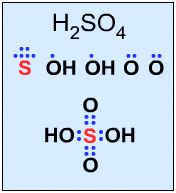
 |
|
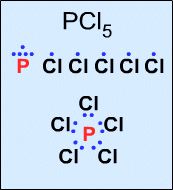
Fourth, determine the "total coordination number" of the central atom, where:
|
|
Fifth, the overall geometry of the atomic centre is determined by the mutual repulsion between the electron pairs of the total coordination number.
|
|
Sixth, there two adjustments are required by the VSEPR method to find the geometry of an atomic centre:
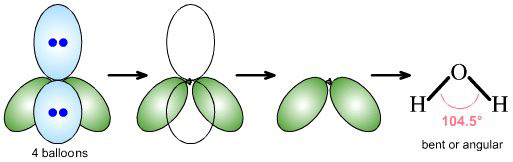 |
By Starjester1 as a Honors Chemistry class project:
The AXE system
American General Chemistry textbooks – but for some reason not British ones – adopt the excellent AXmEn system, where A is the central atom, m the number of ligands X, and n the number of nonbonded lone-pairs of electrons, E, about the central atom.
In this system:
methane, CH4, is AX4
ammonia, H3N:, is AX3E1
water, H2O, is AX2E2
Note that different AXmEndesignations can give rise to the same overall geometry or shape:
For example:
AX2E1 and AX2E2 both give rise to bent or angular geometries
AX2 and AX2E3 both give rise to linear geometries
Patterns in AXE Space
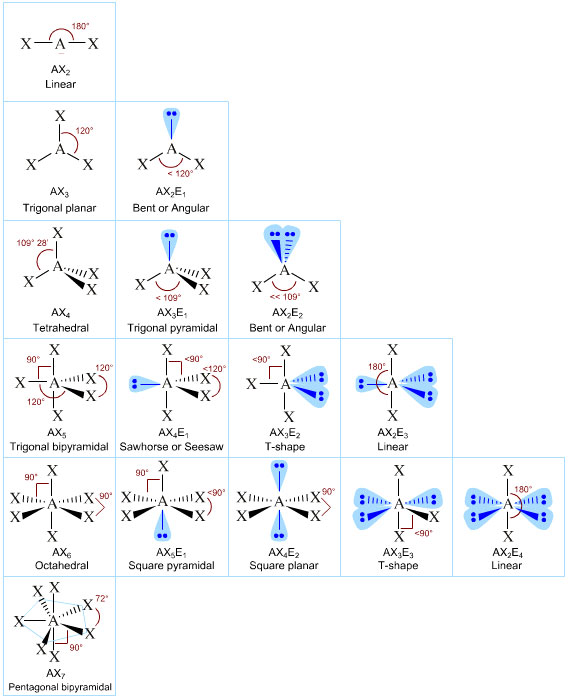
The AXE system gives rise to a pattern, from which the various atomic geometric shapes can be determined/assigned:
A Couple of More Advanced Examples:
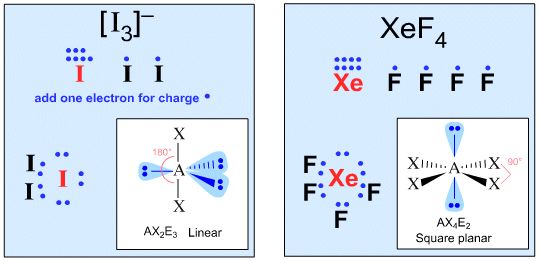
Beyond VSEPRDr. Benjamin R. Martin of the Department of Chemistry and Biochemistry Texas State University, a solid state chemist, writes to point out that there are several extensions to the vanilla VSEPR approach, as described above, that he finds useful:
|
Some Words About The Nature of VSEPR "Theory"
Valence shell electron pair repulsion – extraordinary though this may sound – is not based on any deep theory. It is simply a 'neat trick' that works extraordinarily well; see below.
VSEPR theory only says that ligands arrange themselves about an atomic centres so as to maximise spherical symmetry.
The 'theory' does not in any way explain why non-bonding lone pairs of electrons behave as they do.
It is often said that the VSEPR structure of water shows "two lone pairs of electrons sticking out like a pair of rabbit's ears":
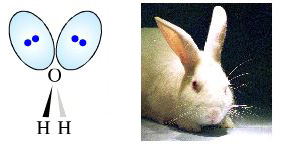
However, these "rabbit's ears" cannot be seen in molecular orbital (MO) theory models of molecular structure, and neither are they employed in the common space-fill molecular representations.
The rabbit's ears are not there!
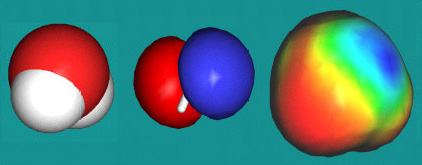
Space fill, HOMO and surface density representations of H2O.
Molecular structure modeling techniques based on quantum mechanics manipulate atomic orbital wavefunctions to maximise spherical symmetry and minimise energy.
According to VSEPR 'theory', a given set of ligands-plus-lone-pairs will arrange themselves about an atomic centre so as to adopt the most spherically symmetric arrangement.
However, there is no theoretical justification for this arrangement within VSEPR. The VSEPR 'theory' is simply a set of rules for predicting the maximum spherical symmetry of electron pairs, which is not the same thing at all.
The spherical symmetry argument is presented in greater detail elsewhere in this chemogenesis web book: Why Chemical Reactions Occur.
Ronald Gillespie, one of the two developers of modern VSEPR theory, ascribes the VSEPR effect to the Pauli exclusion principle: R. Gillespie & P. Popelier, Chemical Bonding and Molecular Geometry, OUP, 2001, Chapter 4 (Amazon).
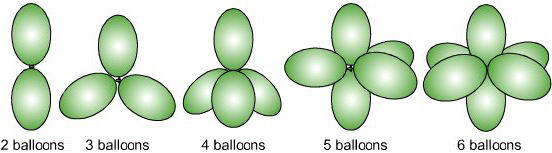
But, the same geometry predictions can be made by quantum mechanical calculations AND the VSEPR technique. This is not the same thing as saying that the VSEPR technique has its roots in QM. VSEPR predictions can be modelled by packing balloons together!
Read more about the nature of chemical theory, with specific reference to VSEPR, in the section of this web book: A Timeline of Structural Theory.
* The above text about the theoretical basis VSEPR was written in 2008, or thereabouts. I have recently, in 2017, been contacted Sam Johnson who writes:
"I think that a fair bit of work has been done that shows that electrons pairs repel each other because same spin fermions avoid each other (ie. the repulsion of electron pairs is the result of the Pauli exclusion principle).
"The statement regarding the lack of evidence for lone pairs in the electron density is misleading: Gillespie and Bader showed that the Laplacian of the electron density shows evidence of both the shell structure and electron pairing. So lone pair are not maxima in the electron density (only nuclei are), but if you look at enough electron density plots of something like water carefully you can actually see the distortions in the electron density without having to resort to the Laplacian.
"The Electron Location Function (ELF) method is a popular way to visualize the impact of the Pauli exclusion principle on the electron density. Gillepsie has written reviews and books regarding these concepts."
The Wikipedia ELF page says: ELF's usefulness stems from the manner it allows the analysis of electron localization in a chemically intuitive way. For example, the shell structure of heavy atoms is obvious when plotting ELF against the radial distance from the nucleus. When applied to molecules, an analysis of the ELF shows a clear separation between the core and valence electron, and also shows covalent bonds and lone pairs, in what has been called "a faithful visualization of VSEPR theory" in action.
Moreover, the ELF picture of water shows the "rabbit's ears" like structure (in orange)...

Symmetry Point Groups and Molecular Geometry
Atomic centres with multiple ligands can be mapped to symmetry point groups, where symmetry point groups are:"Symmetry operations that leave at least one point unmoved and that exhibit translational periodicity." From MathWorld, combining statements from here and here.
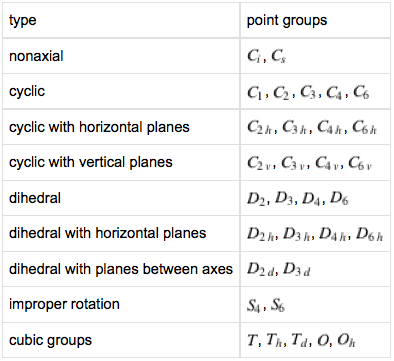
Symmetry point groups and the associated group theory are used for:
Understanding crystal structure
Classifying molecular structures
Classifying molecular orbitals
Constructing hybrid molecular orbitals
Classifying modes of vibration
Predicting allowed spectral transitions and splitting patternsAbout 40 point groups suffice to classify all known molecules.
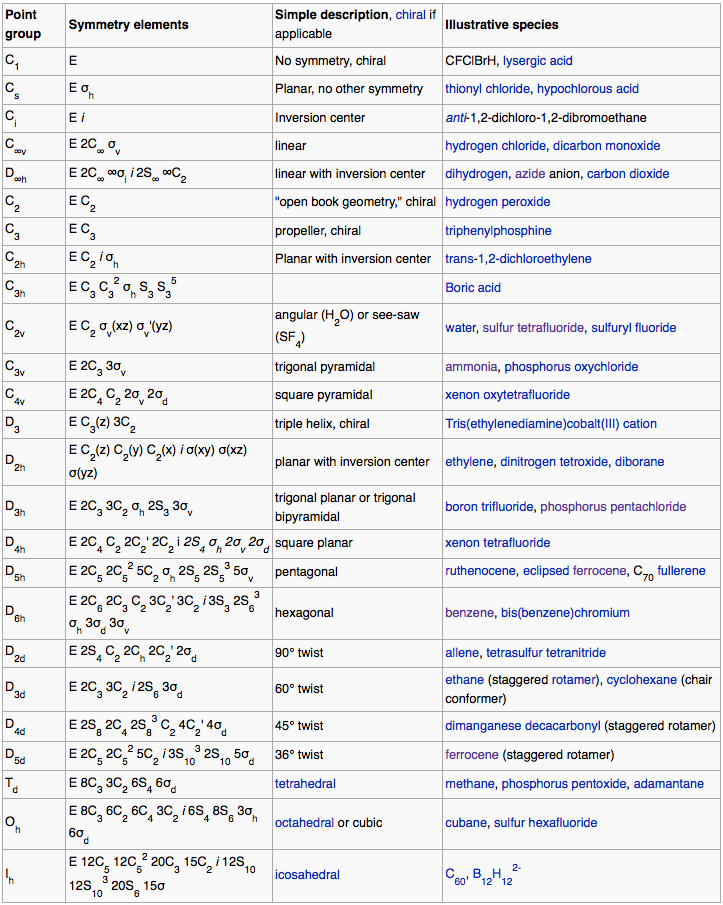
Keeping things simple, and maximizing symmetry by making all ligands identical, the symmetry point groups associated with VSEPR geometries are:
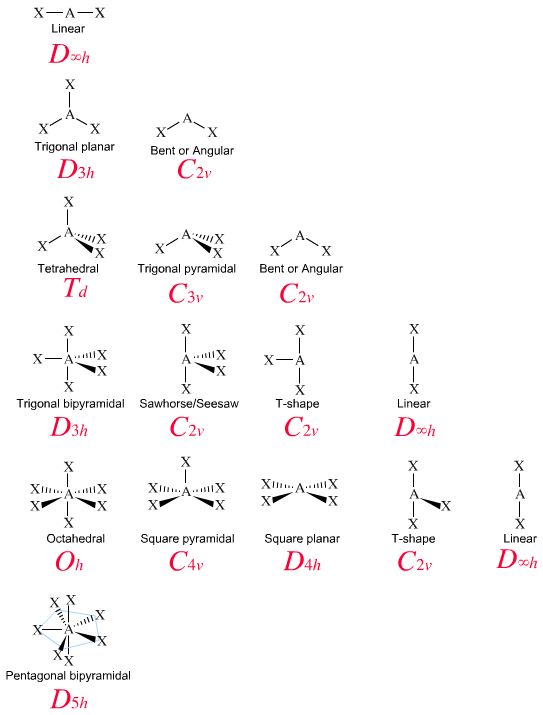
Henry Rzepa (of Imperial College London) has developed an excellent Overview of Molecular Symmetry Operations and Symmetry Groups web site that deals with these issues in detail.
And, there is an excellent Wikipedia page on molecular symmetry:
Distortions
In the real world molecules and molecular ions are subject to various types of distortion that act to reduce symmetry:
Consider the molecular entities methane, fluoromethane, difluoromethane and bromochlorofluoroiodomethane:
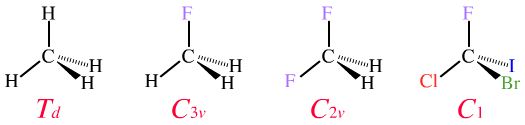
Formally these four molecules have different symmetries and belong to distinct symmetry point groups. That said, chemists usually consider the central carbon atoms of all four of these molecules as being "tetrahedral", but only methane is perfect.
X-ray structures are determined on solid phase materials, and crystal packing considerations often distort molecules and molecular ions and reduce symmetry. The CoolMolecules Molecular Structure Explorer website, where all structures are based on actual experimental data, illustrates this point: check out the bond length and H-N-H bond angle data of the ammonium ion, [NH4]+, below (image captured from the CoolMolecules site):
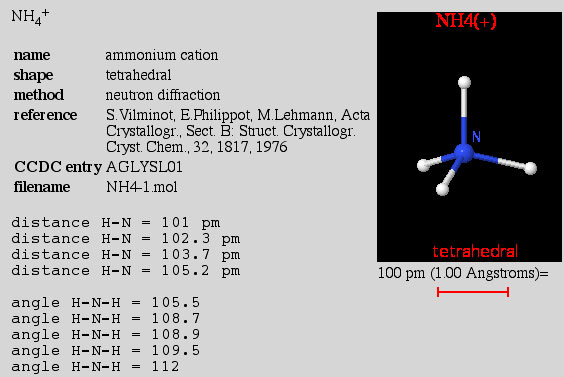
The CoolMolecules site classifies molecules by the shape/geometry of the central atom and not by the symmetry point group.
High symmetry entities like the ammonium ion, [NH4]+, are more likely to be found in the liquid phase where absolute proof of geometry/symmetry is difficult.
in silico computational chemistry structure calculations have a strong propensity to maximise symmetry, sometimes incorrectly!
The VSEPR drills on the Chemistry & Tutorials & Drills web site, another meta-synthesis web site, employ pure symmetry molecules and molecular ions.
Most of the VSEPR examples used in the Chemical Thesaurus are geometrically pure.
Many heavy metal complexes and complex ions are susceptible to Jahn-Teller distortions:
"A non-linear molecule in an electronically degenerate state must distort to lower the symmetry, remove the degeneracy, and lower the energy". Jahn and Teller, Proc. Roy. Soc., 1937, A161, 220
Hybridization & π-Bonding
VSEPR does not model the π-bond. However, an alliance can be made between valence bond (VB) theory, Hückel MO theory of π-systems and VSEPR.
Hückel structures such as the alkene π-bond can be superimposed onto the underlying VSEPR hydrocarbon sigma-skeleton.
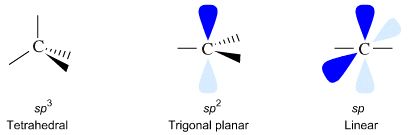
Valence bond theory takes an atom's atomic orbitals (AOs) and hybridizes or 'mixes' them together. With carbon there are three possibilities and three associated geometries.
| s + p + p + p | → | sp3 + sp3 +sp3 +sp3 | "sp3 hybridized" | tetrahedral |
| s + p + p + p | → | sp2 + sp2 + sp2 + p | "sp2 hybridized" | trigonal planar |
| s + p + p + p | → | sp + sp + p + p | "sp hybridized" | linear |
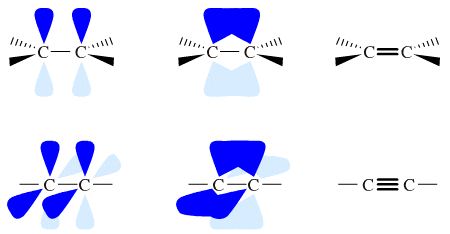
Two sp2 hybridized carbons plus associated electrons are able to join together to give an alkene type π-bond, C=C. Two sp hybridized carbons join to give a 'triply bonded' alkyne (acetylene):
The sp3, sp2 and sp hybridized atomic centres together with the AXE atomic centres of VSEPR make up the chemist's toolbox of atoms and atomic centres that can be constructed into molecules and molecular ions.
For example, the difunctional molecule 3-amino-1-propene has a primary amine function modelled as an AX3E1atomic centre with a lone pair of electrons, and an alkene constructed from two sp2 hybridized atoms with a pair of electrons in the π-molecular orbital:
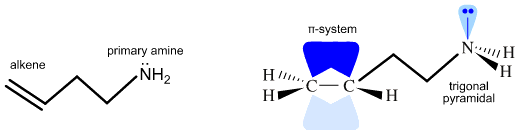
Valence bond theory and VSEPR both predict methane to be tetrahedral, even though the methodologies are totally different: valence bond theory directly manipulates the atomic orbitals while VSEPR simply says that the methane will adopt the most spherically symmetric conformation.
Ammonia, H3N:
In the gas phase ammonia – uniquely– is a very strange entity indeed.
To the chemist, ammonia, H3N:, has a trigonal pyramidal shape that is able to [classically] invert "like an umbrella in the wind" between two forms: a "down pyramid" form and an "up pyramid" form. Each of these trigonal pyramidal forms has C3v point group symmetry.
From a quantum-mechanical point of view, the ground state of ammonia, H3N:, is a superposition of the "down pyramid" and the "up pyramid". (VSEPR is not a QM theory.)
Because of the low mass of the hydrogen atom and the nature of quantum mechanics, ammonia is "simultaneously" in both configurations, but if ammonia's configuration is measured, it will always be found in one trigonal pyramidal configuration or the other.
Like the famous double slit experiment of quantum mechanics, where a wave/particle passes through two slits simultaneously yet measurement will always show a discrete particle going through just one slit, ammonia's ground state can not be fully described with a classical "ball-and-stick" model.
Thus, it can be argued that ammonia actually has a planar D3h symmetry, as proved by the operation of the ammonia maser.
What You Need To Know
To be proficient in chemistry at the university entrance level [ American AP, British AS/A2 or French Baccalaureate] it is absolutely essential to be able to recognise the VSEPR geometries, know the associated names and work out VSEPR structures from formula of the AEX systems listed below:
AX2
AX3
AX4
AX5
AX6
AX3E1
AX2E2
At university chemistry level, all of the above atomic centre geometries (plus associated point groups) should be known.
This page is concerned with the geometries of ligands about single atomic centres, and to help this understanding a series of drills have been developed to test your knowledge.
Searches for real chemical entities based on VSEPR geometry can be made using the web based Chemical Thesaurus reaction chemistry database.
The CoolMolecules Molecular Structure Explorer website classifies molecules by the shape/geometry of the central atom, and all structures are all obtained from experimental data. Searches on the extensive database can be made by atom, shape, experimental method and molecules can be rotated. Highly recommended.
 |
 |
 |
| Modern Lewis Theory | Diatomics & MO Theory |
© Mark R. Leach 1999 –
Queries, Suggestions, Bugs, Errors, Typos...
If you have any:
Queries
Comments
Suggestions
Suggestions for links
Bug, typo or grammatical error reports about this page,please contact Mark R. Leach, the author, using mark@meta-synthesis.com
This free, open access web book is an ongoing project and your input is appreciated.