Periodic Table |
 |
 |
 |
 |
 |
 |
 |
| Gibb's Build-a-reaction | Modern Lewis Theory |
Timeline of Structural Theory
|
"The
nature of the chemical bond is the problem at the heart of all chemistry"
Bryce L. Crawford Jr. |
In large part the science of chemistry is concerned with modeling the chemical
structure of matter and understanding the nature of the chemical bond. However,
the chemical bond sits right on the boundary between the classical
and quantum mechanical worlds and academics, professional chemists and teachers
liberally pick ideas, concepts and models from both. To understand the nature
of chemical bonding it is necessary to see how the various ideas have developed
over the past 200 years. This page introduces the main theoretical approaches
to understanding chemical structure and reactivity, places them in historical
context and considers them with reference to each other.
Introduction
When chemists think about the structure and behaviour of a substance like ammonia, NH3, they are influenced by experimental (empirical) evidence, physical theory, the history of science, educational dogma and philosophical position.
There are three general approaches to understanding a substance such as ammonia, NH3:
Empirical study is concerned with observation and experiment rather than explanation and theory, but theory may guide experiment and experiments often lead to the development of new theory.
Classical Theory & Newtonian Mechanics model the chemical world in terms of scaled down, ideal macroscopic objects: colliding spheres, bending rods, rotating joints, etc.
Quantum Mechanical theories are concerned with low mass, fast moving photons and electrons that exhibit wave-particle duality.
Chemistry sits right on the boundary between the quantum and classical worlds: the chemical bond is a quantum mechanical construct but the behaviour of molecular entities can often and conveniently be described in classical terms. As a result we have two entirely different types of model of chemical structure, bonding and reactivity.
- On one hand, we
have theories that treat electrons as countable dots and stress the
importance of electron accountancy. These "Lewis" models recognise
– but cannot explain – the magic numbers of electrons associated
with the group 18 elements (He, Ne, Ar, Kr, Xe), aromatic π-systems,
18-electron transition metal complexes, etc. Models include: Lewis octet
theory, Lewis acids/base theory, electron accountancy, reactions mechanisms
& curly arrows, VSEPR, molecular mechanics, etc. While the various
Lewis electron accountancy models work most of the time, they do not
work all the time. Lewis theory cannot explain atomic or molecular spectroscopy
or why oxygen, O2, is paramagnetic.
- On the other hand,
we have quantum theory and models derived from the Schrödinger
wave equation. These wave mechanical approaches lead to atomic orbitals,
molecular orbital theory, valence bond theory and FMO theory. The MO
approach has been developed into software such as Gaussian and Spartan. Quantum chemistry
techniques give good numerical answers, but they are conceptually difficult.
- Students tend to
be introduced to chemistry through the various Lewis models... and are
then surprised to learn they that these models are not the whole story
and can even be wrong.
The diagram below shows a timeline of the development of the main theoretical chemical structure and reactivity ideas over the last 200 years:

The red arrows in the diagram are used to represent the act of "conversion from quantum to classical". They are used twice, between the Bohr atom and Lewis theory, and between VB theory and VSEPR theory. On both occasions there is a theoretical leap of faith because the impression is given that Lewis theory and VSEPR theory are based upon quantum theory, when they are not.
Timelines: A Proviso One reader of this page has pointed out that the irresistible temptation to show the logical development of a subject using timelines does not represent the actual history, which is never neat & tidy. Read more on John Denker's website. |
1803: John Daltonargued – on the 21st of October 1803 to the Manchester Literary and Philosophical Society in Manchester, and I am writing this text on the 200th anniversary and less than a mile away – for the atomic theory originally proposed by the Greeks. Dalton defined an atom as the smallest part of a substance that can participate in a chemical reaction. He proposed that elements are composed of identical atoms and that elements combine in definite proportions, stoichiometry. Dalton also produced an early table of atomic weights.
1869: The Mendeleev Tablelle I, the first plausible periodic table, was published. It was constructed using the recently discovered element, stoichiometric and periodicity data because some 35 elements had been discovered since 1800.
The success of this first version can be attributed to the gaps which Mendeleev correctly predicted would contain undiscovered elements, and he predicted their properties.
To the modern eye, the biggest omissions are the the Group 18 rare gases (He, Ne, Ar, K & Xe) and that only a small number of f-block elements are shown.
Of more importance, however, is that the elements are arranged by mass rather than atomic number, a concept had yet to be discovered so Mendeleev can be forgiven.
The 1869 Tabelle I is a quite remarkable construct:

1896: Radioactivity is a window into atomic structure.
In the year 1904, JJ Thomson proposed that the atom had a "plum pudding" structure, with the negative electrons in circular arrays – the plums – embedded in a spherical pudding of positive charge with mass evenly distributed. It was the study of radioactivity, in particular alpha radiation, that enabled Rutherford to develop his experiments to probe atomic structure.
March 1904 edition of the Philosophical Magazine JJ Thomson writes: "... the atoms of the elements consist of a number of negatively electrified corpuscles enclosed in a sphere of uniform positive electrification, ..."

Diagram from Wikipedia & Charles Baily's presentation: here. The lower depictions are incorrect, in the sense that they are not true to the model proposed by Thompson in 1904.
Elements and Atoms: Case Studies in the Development of Chemistry
Carmen Giunta of Le Moyne College Department of Chemistry has collected many of the original papers plus commentary dealing with eighteenth and nineteenth century science in a web book called Elements and Atoms: Case Studies in the Development of Chemistry. This web resource is highly recommended:

1900: Planck' Quantum Idea was developed as a way of explaining black body radiation and the associated ultraviolet catastrophe, by proposed that energy energy comes in small packets or quanta.
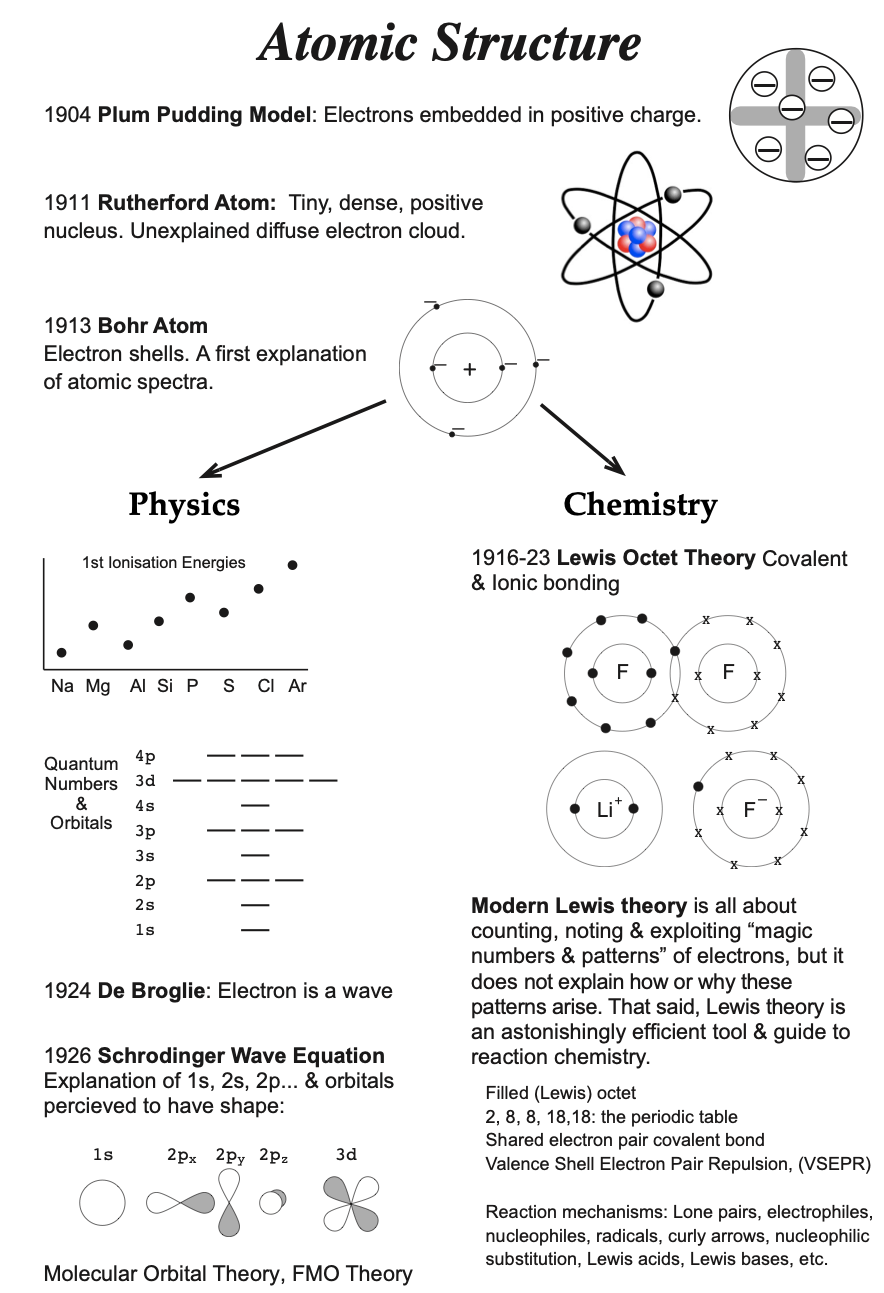
Planck's constant is:
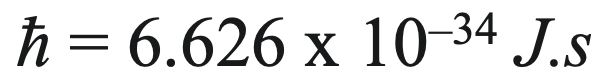
1905: Einstein and the Photoelectric Effect It was known from experiment that metals emit electrons when exposed to light (the system has to be in a vacuum), however, it could not be explained why the rate of emission depended upon the wavelength of the light in the way that it did. In 1905, Einstein showed that if light consisted of particle-like quantised photons, where the energy of the photon depended upon its wavelength, the photoelectric effect could be explained. This work led to a revolution in the understanding of both the electron and light. Light could behave as both a wave and a particle, depending upon the experiment. It was for this work that Einstein received the Nobel prize.
1911: Rutherford, already a Nobel prize winner (1908), interpreted the results of the Geiger-Marsden experiment involving a beam of alpha particles fired at a thin foil of gold designed to measure the deflection as the alpha particles interacted with the "plum-pudding" gold atoms.
Rutherford was astonished with the results which showed that most of the alpha particles passed straight through the gold foil unaffected, but a small minority were deflected by large angles. Rutherford commented at the result: "It was almost as incredible as if you fired a fifteen-inch shell at a piece of tissue paper and it came back and hit you".
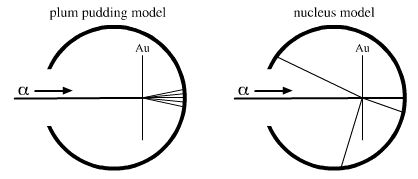
Rutherford proposed a model of the atom had a very small, dense, positively charged nucleus surrounded by electrons.
The HyperPhysics website has a nice diagram comparing the tiny size of the nucleus and the size of a gold atom with the sizes of the Sun and the solar system. This is our version of the diagram, converted to metric units:

The "Rutherford Atom" has developed into a model that is still widely used, although the artists impressions hugely distort the relative sizes of the various atomic components (much to this author's annoyance!):
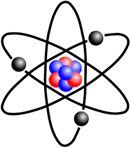 |
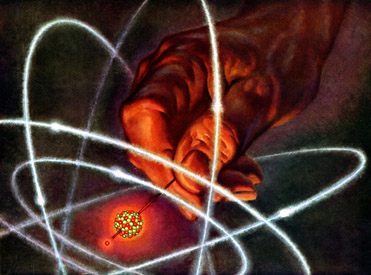 |

Our story now moves on from atomic structure to how the negative electrons 'associate' with positive nucleus.
1913: The Bohr Atom In 1913 Niels Bohr - while working in Rutherford's laboratory - constructed a model of the atom that had small, light, fast, particle-like, negatively charged electrons "orbiting" a small, massive positively charged nucleus... although the reason why the electron did not spiral into the nucleus could not be explained. The electron shells were quantised, and as the electrons moved from shell to shell they emitted or absorbed photons the energy of which was equal to the energy difference between the shells.
The Bohr model is the first plausible model of the atom and it is still widely used in education, particularly in illustrations because it is so easy to draw and understand.
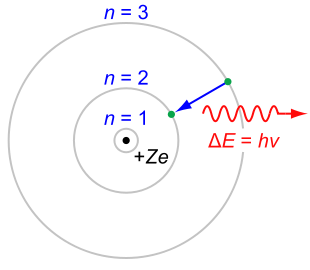
Diagram from Wikipedia: "The Rutherford-Bohr model of the hydrogen atom (Z = 1) or a hydrogen-like ion (Z > 1), where the negatively charged electron confined to an atomic shell encircles a small positively charged atomic nucleus, and an electron jump between orbits is accompanied by an emitted or absorbed amount of electromagnetic energy (hν). The orbits that the electron may travel in are shown as grey circles; their radius increases as n2, where n is the principal quantum number. The 3 → 2 transition depicted here produces the first line of the Balmer series, and for hydrogen (Z = 1) results in a photon of wavelength 656 nm (red)."
Atomic Modeling in the Early 20th Century: 1904-1913 Charles Baily, University of Colorado, Boulder This excellent Power Point presentation – now as a .pdf file – discusses:
Personal communication: There is an associated paper by Charles Baily with the same title presented at the 24th Regional Conference on the History and Philosophy of Science, Boulder, CO (10/12/08). |
1916: Lewis Theory was developed at UC Berkeley by the active research group led by G.N.Lewis. The theory was first published in 1916 and was expanded in book form in 1923.
Lewis used the new ideas about atomic structure that were widely discussed in his labs:
- atomic number
- Bohr atom
- developing periodic table
- crucial importance of the electron
- chemistry of ionic solutions
- molecular structure
- etc.
Lewis proposed the two electron chemical bond, later named the covalent bond by Langmuir. Linus Pauling supported the Lewis analysis.
Students of chemistry first learn about Lewis through the well known (some would say too well known) Lewis Octet Rule. This extraordinarily useful rule of thumb states that atoms like to have a full octet of eight electrons in their outer or valence shell. The argument is that fluorine, with seven electrons 'wants' another electron to give the stable 'full octet' fluorine ion, F–. Likewise, sodium loses an electron to give the sodium ion, Na+, another species with a full octet. Students soon realise that 8 is not the only special number. Phosphorus pentachloride, PCl5, has 10 electrons. Benzene has 6 electrons in its aromatic π-system. Transition metal complexes often follow the 18 electron rule. Etc.
The Lewis model in its modern form is widely taught in schools and at university level, even though Lewis's electrons are entirely classical:
Negative electron dots are simply assigned to atomic shells, covalent bonds or lone pairs, where they are counted against positive nuclear charge.
In essence, Lewis 'octet' theory is electron accountancy with magic numbers:
The 'theory' gives absolutely no explanation as to why the numbers of electrons about an atomic centre: 2, 8, 8, 18, 18, 32, should exhibit such special stability.
Yet, Lewis theory and electron accountancy are the key tools used by most chemists most of the time to help understand structure and reactivity.
Some examples of Lewis theory in action:
- Lewis theory that it can be superimposed upon Mendeleev’s Periodic Table where it explains vast amounts of structural and reaction chemistry:
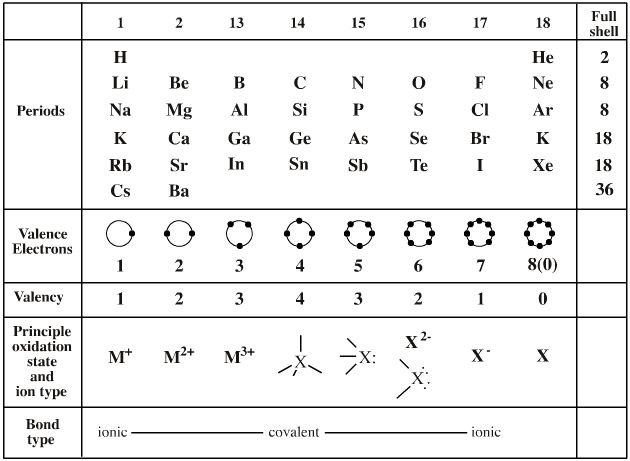
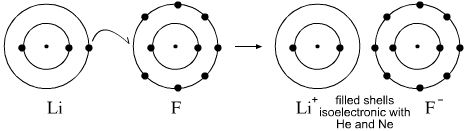
- Lewis theory can be used to describe and explain the reaction between lithium and fluorine to give lithium fluoride, where the Li+ ion is isoelectronic with He and F– is isoelectronic with Ne:
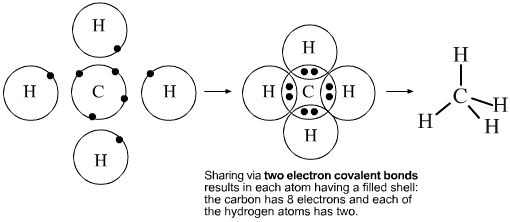
- Lewis theory can be used to describe and explain the molecular structure of a substance methane, CH4. The Lewis argument is that carbon has 4 electrons in its valence shell, and four hydrogens each with one electron in their valence shell. These combine to give CH4 in which electrons are shared between atoms. In the Lewis structure, each hydrogen has two electrons in its valence shell, and the carbon eight. The Lewis structure maps straight onto the VSEPR (AX4) structure:
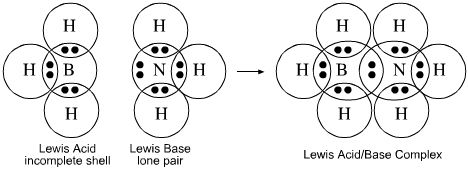
- Lewis theory, electron accountancy and magic numbers can be used to describe and explain the structure and reactivity of many reactive species, including Lewis acids and Lewis bases such as borane, BH3, and ammonia, NH3. Borane, BH3, has only six electrons in its valence shell, but it wants eight and it is an electron pair acceptor. Ammonia, NH3, has a full octet, but two of the electrons present as a reactive lone-pair. Borane reacts with ammonia to form a Lewis acid/base complex in which both the boron and the nitrogen atoms no have a full octet. No explanation is given within Lewis theory as to why the number eight should be so important:
- Lewis theory, electron accountancy and magic numbers are used to explain most types of reaction mechanisms, including Lewis acid/base, redox reactions, radical, diradical and photochemical reactions. Whenever a curly arrow is used in a reaction mechanism, Lewis theory is being evoked. Do not be fooled by the sparse structural representations employed by organic chemists, curly arrows and inter converting resonance structures are pure Lewis theory:
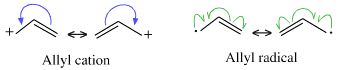
Valence Shell Electron Pair Repulsion, below and in detail here, is an extension of Lewis theory.
Lewis theory is good at describing:
Much atomic, ionic and molecular structure
Electron accountancy during chemical reactions
Reaction mechanisms with curly arrows
Maps to VSEPR theory (below)
Lewis theory is very accommodating and is able to 'add-on' those bits of chemical structure and reactivity that it is not very good at explaining itself. Consider the mechanism of electrophilic aromatic substitution, SEAr:
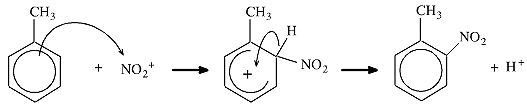
The diagram above is pure Lewis theory:
- The toluene is assumed to have a sigma-skeleton that can be described with VSEPR.
- The benzene π-system is added to the sigma-skeleton, but it is really a Lewis construct when described as "planar, cyclic and containing six π-electrons". Six is a magic number.
- The curly arrows are showing the movement of pairs of electrons, pure Lewis.
- The Wheland intermediate is deemed to be non-aromatic because it does not possess the magic number six π-electrons.
In Lewis theory, benzene's six π-electrons have exactly the same status as neon's eight electrons. Both are magic numbers associated with stability, but no explanation is given as to why this should be so.
Lewis theory is bad at explaining:
The nature of the covalent bond
Why oxygen, O2, is a magnetic diradical
The hydrogen bridge bond found in diborane, B2H6
π-systems
Transition metal chemistry
Read more about Lewis structures and the relationship between Lewis theory and other structural theories in an excellent page by physicist John Denker.
1913-25: Spectroscopy & Quantum Numbers Atomic spectra had been taken since the 1850s by scientists like Bunsen and Kirchhoff. In Denmark, Niels Bohr re-studied atomic spectra and - along with Sommerfield, Stoner and Pauli - devised the quantum numbers from empirical (spectroscopic) evidence:
n principal
l subsidiary (azimuthal, angular momentum or orbital shape)
ml magnetic
ms spin
After the discovery/invention of the Schrödinger wave equation, below, and quantum field theory in the 1930s, the Bohr model became known as the old quantum theory, Wikipedia.
|
Question: Is light made of waves or particles? Answer: Both Experiments that explore the wave-nature of light show light to be wavelike... and experiments that demonstrate that light is made of discrete photons show that light is indeed constructed from particles. Weird. Yeah, we know. Just get used to it. Light is said to exhibit 'wave-particle duality'. In 1924 de Broglie's proposed that all moving particles has a wavelength is inversely proportional to momentum and that the frequency is directly proportional to the particle's kinetic energy (Wikipedia):
This concept leads to one of the most important ideas in 20th century science:
|
1926: The Schrödinger Wave Equation
Edwin Schrödinger knew of de Broglie's proposal that a electrons exhibited wave-particle duality. With this idea in mind, he devised/constructed a differential equation for a wavelike electron resonating in three dimensions about a point positive charge.
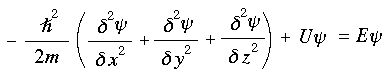
Solutions to the Schrödinger wave equation - resonance modes described by mathematical wavefunctions - assumed discrete, quantised, energies which corresponded to spectral lines of one electron atoms and ions: H•, He+, Li2+ etc., and they corresponded exactly with Bohr's quantum numbers. This development lead to quantum mechanics.
Waves and the the mathematical functions that describe them: wavefunctions, are well understood mathematically. For example, they can be added together or subtracted from each other. Consider two sine waves and their superposition, here:
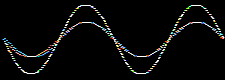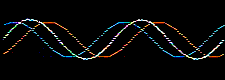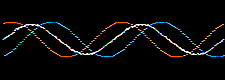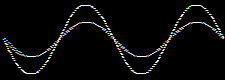
The atomic orbitals derived from the Schrödinger wave equation, being waves, can be added together. The arithmetic can be carried out in various ways.
The term "wavefunction" can be interchanged with term "orbital". By convention, mathematical expressions are termed wavefunctions and chemical structure and structure and reactivity are discussed with reference to orbitals.
Atomic Orbitals are constructed from the four quantum numbers. The AOs fill with electrons, lowest energy AO first, the aufbau principle. An orbital can contain a maximum of two electrons, and these must be of opposite spin, the Pauli exclusion principle. One final rule, Madelung's rule points out that the orbitals fill with electrons as n + l, as principle quantum number plus subsidiary quantum number, rather than n.
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < 5d < 6p < 7s < 5f < 6d < 7p

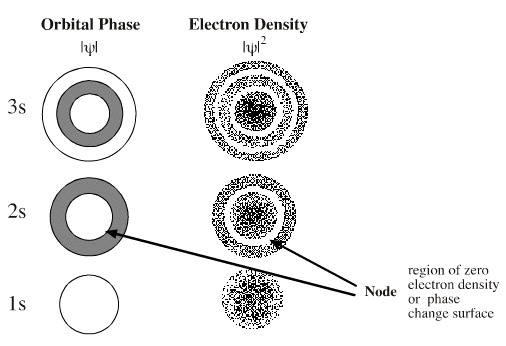
Orbitals shape and phase. s-Orbitals are radial and they have n-1 (n minus one) nodes, where n is the principal quantum number. Thus, the 1s orbital is devoid of nodes, the 2s orbital has one node, etc. The s-orbital nodes are spherical and they are best viewed in cross section (below). There is a change of phase at the node. Max Born suggested that the squared wavefunction equates electron density, but squaring results in the loss of all phase information.
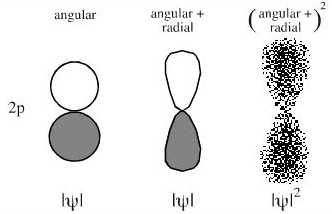
p-Orbitals have both radial and angular components and have a "figure of 8" shape.
1928: Pauling's Five Rules: Crystal Structure
The crystal structure of an ionic compound can be predicted using a set of empirical rules:
- The First Rule: Around every cation, a coordination polyhedron of anions forms, in which the cation-anion distance is determined by the radius sums and the coordination number is determined by the radius ratio.
- The Number of Polyhedra with a Common Corner - The Electrostatic Valence Rule: An ionic structure will be stable to the extent that the sum of the strengths of the electrostatic bonds that reach an anion equals the charge on that anion.
- The Sharing of Polyhedra Edges, Faces & Corners, particularly faces by two anion polyhedra, decreases the stability of a crystal.
- An extension of the third rule: In a crystal which contains different cations, those with high charge and low coordination numbers tend not to share elements of their coordination polyhedra.
- The Rule of Parsimony The number of essentially different kinds of constituents in a crystal tends to be small.
Crystal structures are usually named after a definitive crystal structure, such as: zinc sulfide (structure), sodium chloride, cesium chloride, calcium fluoride (fluorite), rutile, diamond, etc.
Read more in the Wikipedia and ScienceWorld.
1932: Pauling's Electronegativity Linus Pauling used empirical heat of reaction data to introduce the elemental property of electronegativity which he defined as: "The desire of an atom to attract electrons to itself".
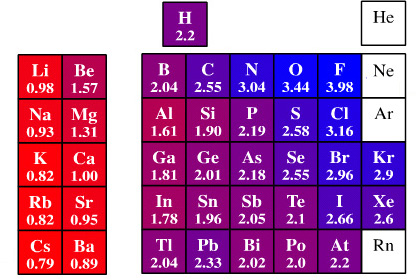
Electronegative elements, such as fluorine, "want" electrons so they can form negative ions while electropositive elements, such as cesium, like to lose electrons and form positive ions.
The great befit of electronegativity is that the numbers can be used to quantify this effect and predict bond dipole moment (polarity) and degree of ionic character. For example: fluorine (3.98) is electronegative and cesium (0.79) electropositive. CsF is strongly polarised Cs+ F– and is 89% ionic.
1930: Valence Bond Theory Once atomic orbitals were understood in terms of both Bohr's quantum numbers and the Schrödinger wave equation, the quest was on to understand bonding in molecules. Linus Pauling's approach was to take the atomic orbitals and mix (hybridize) them together. For example, the 2s orbital can mix with the three 2p orbitals to give four "hybrid" sp3 orbitals which are arranged tetrahedrally about the central atom.
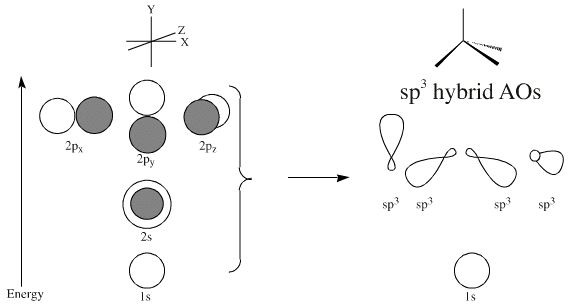
Thus, hybridization can rather easily explain the tetrahedral geometry of methane. Valence bond theory can also explain why the carbons in ethene (ethylene) are triangular planar by invoking sp2 hybridization and why ethyne (acetylene) is linear: sp hybridization.
VB theory also introduces the concept of "resonance", an idea dependent upon electronegativity. For example, chlorine is more electronegative than hydrogen and the compound hydrogen chloride, HCl, is polarised H+Cl–. VB theory suggests the various possible forms are in resonance.
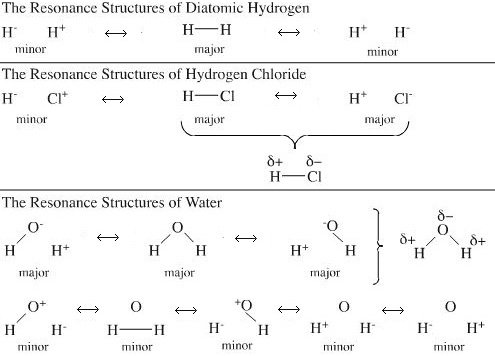
VB theory is widely employed in education because it produces easily understandable structures. However, the mathematics of orbital manipulation is easier if non-hybridized orbitals are employed. For this reason VB theory has become something of a theoretical "dead end" compared with MO theory.
Read more about the valence bond approach to understanding polyatomic structure here.
Molecular Orbital Theory assumes that molecules are multi-nucleated atoms: the molecular orbitals, MOs, are assumed to encompass the two nuclei. Electrons are added to the MOs using the same rules that are used to add electrons to atomic orbitals: the aufbau principle and the Pauli exclusion principle. MOs have a similar geometry to atomic orbitals, but are more involved. The MO approach is most obviously seen and understood with diatomic molecules, H2, N2, etc.
The MO approach to diatomic hydrogen places the two nuclei (protons) close to each other. An electron is added to the lowest energy MO, the sigma bonding MO. The second electron also goes into the sigma MO. The third electron goes into the next MO which has a node between the two nuclei (a region of zero of electron density) and is called the "sigma star" antibonding MO.
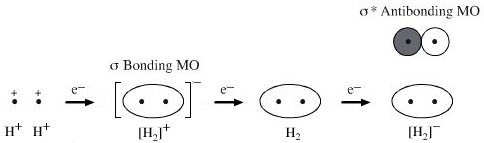
However, the all encompassing MO approach is difficult to apply to molecules with many atoms. The 'trick' is to use the Linear Combination of Atomic Orbital (LCAO) simplification in which atomic orbitals are added together to form molecular orbitals. Hydrogen is constructed by adding two 1s orbitals into a 1 sigma MO.

The interaction of atomic and molecular orbitals can be represented in MO Energy diagrams:
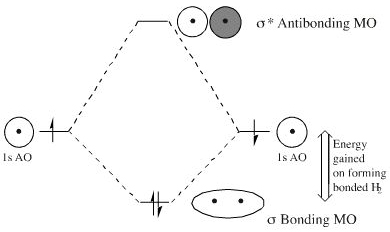
There are various possible AO to MO interactions:
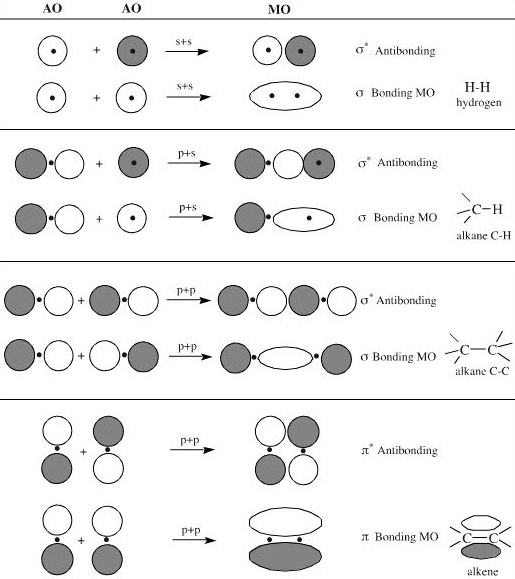
The LCAO approach has been highly developed in software. The AOs are described in terms of "basis functions", such as finite elements, Gaussian type orbitals (GTOs) or Slater type orbitals (STOs). (For historical reasons basis functions are called basis AOs. Such ab initio (or "from the start") software is able to calculate molecular geometry and energy to high precision. Commercial software is available.
Read more about diatomic molecules and polyatomic molecules elsewhere in the chemogenesis web book.
1937/9: Hellmann-Feynman Theorem Wikipedia
The Hellmann-Feynman theorem states that once the spatial distribution of electrons has been determined by solving the Schrödinger equation, all the forces in the system can be calculated using classical electrostatics.
Thus classically, the equilibrium configuration of a molecule like H2, (H–H, bond length 74 pm) has the resultant force acting on each nucleus vanishing. The electrostatic (++) repulsion between the two positive nuclei is exactly balanced by their attraction to the electrons between them.
The Hellmann-Feynman theorem was discovered independent by Hans Hellmann (1937) and Richard Feynman (1939).
1943: Valence Shell Electron Pair Repulsion (VSEPR) states that electron pairs (both bonded covalent electron pairs and nonbonded "lone-pairs" of electrons) repel each other. Methane, CH4, has four bonded electron pairs and these repel each other to give the four hydrogens tetrahedral geometry about the central carbon. Likewise, ammonia has three bonded electron pairs and one lone pair which mutually repel each other so that ammonia is trigonal pyramidal.
Geometry can be predicted using the "AXE" system where A is the central atom, X the number of (electron pair bonded) ligands and E the number of lone pairs.
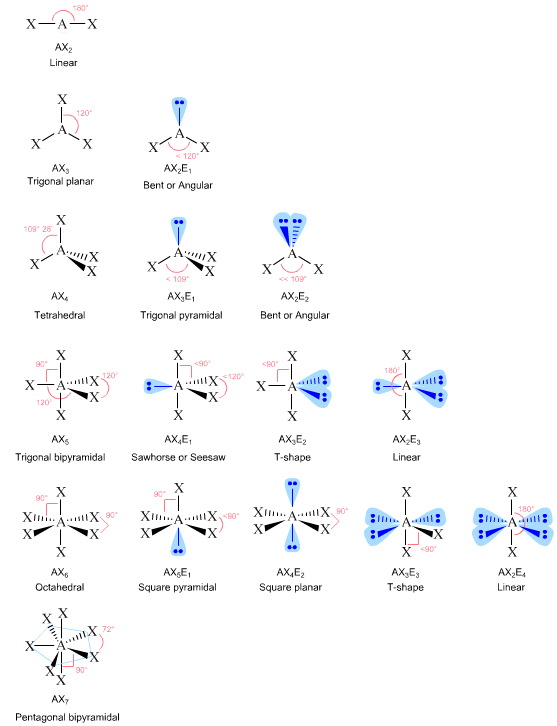
There are two VSEPR explorers on the web, The Chemical Thesaurus here and Cool Molecules here.
Read more about VSEPR theory here, and test your knowledge of VSEPR by going to the Chemistry Tutorials & Drills web site.
|
The relationship between VB theory and VSEPR is interesting in that VSEPR seems to grow out of VB theory. However, VB theory is a wave mechanical theory whereas VSEPR assumes that bonds and lone pairs are entirely classical and says nothing about how the bonding actually occurs. When moving from VB to VSEPR, it is as if the wave mechanical electron bonding becomes fixed in space... in rather like the image on photographic film becomes fixed during the development process. There is no deep theoretical justification to VSEPR theory, other than it predicts an atomic centre will arrange its ligands so that it will assume a geometry with the maximum spherical symmetry. VSEPR theory is "pulled out of a hat", however, as a method it is very successful. |
1960s: Frontier Molecular Orbital Theory was developed in the 1960s by Kenichi Fukui who recognised that chemical reactivity can often be explained in terms of interacting Highest Occupied MOs (HOMOs), Lowest Unoccupied MOs (LUMOs) and Singly Occupied MOs (SOMOs).
- HOMO + LUMO → bonding MO
- HOMO + HOMO → antibonding MO
- LUMO + LUMO → null interaction (no electrons)
- SOMO + SOMO → bonding MO
The FMO approach was developed by Woodward & Hoffmann in the late nineteen sixties who used it to explain an apparently diverse set of reactions involving π-systems, including Diels-Alder cycloaddition, here. Hoffmann used the approach to explore transition metal complexes.
1941: van Arkel-Ketelaar Triangle recognises three extreme types of bonding: metallic, ionic and covalent and that many bond types are intermediate between the extreme types. This behaviour can be rationalised in terms of electronegativity.
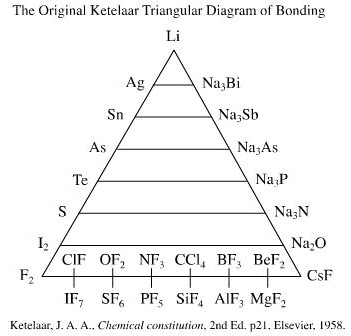
Read in detail about the van Arkel-Ketelaar Triangle in detail elsewhere in this web book.
1993 & 2008:Tetrahedron of Structure, Bonding & Material Type Michael Laing expanded the van Arkel-Ketelaar triangle into a tetrahedron by separating covalent bonding into two types: molecular and network covalent, although Laing uses the terms "van der Waals" and "covalent":

M. Laing, A Tetrahedron of Bonding, Education in Chemistry, 160 (1993)
Molecular covalent materials consist of small molecules with strong intramolecular covalent bonds but weak van der Waals intermolecular attraction. Methane and ammonia are molecular materials.
Network covalent materials have strong covalent bonds which extend throughout the material, examples include: diamond, silica and phenolic resins.
Mark R Leach has recently, 2008, quantified the tetrahedron of structure, bonding & material type with respect to valency and electronegativity:

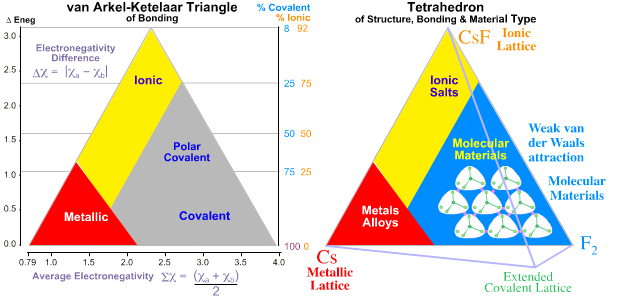
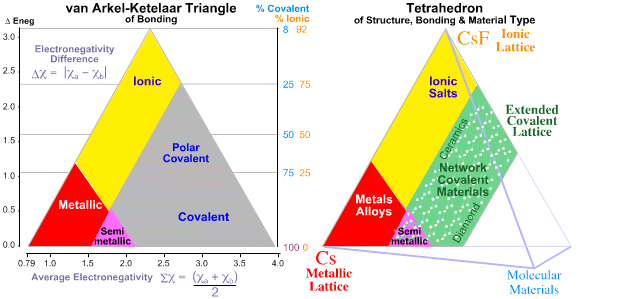
Read in detail about the Tetrahedra of Structure, Bonding & Material Type in detail elsewhere in this web book.
1970s: Molecular
Mechanics and Molecular Dynamics
Valence Shell
Electron Pair Repulsion (VSEPR) theory has been extensively parameterised
and developed into computer software. The method treats a molecule as
a collection of particles held together by elastic or simple harmonic
forces. These forces can be described in terms of potential energy functions.
The sum of these terms gives the overall steric energy. This system can
be modeled by the Westheimer equation is:
Etotal = Es + Eb + Ew + Enb
- Es = energy of bond deformation (stretching or compression)
- Eb = energy of bending
- Ew = torsional energy
- Enb = nonbonded (van der Waals) interactions
D.B. Boyd and K.B. Lipkowitz, Molecular Mechanics: Method and Philosophy, J.Chem.Educ. 59 4 269-274 (1982), P.J. Cox, Molecular mechanics: Application , J.Chem.Educ. 59 4 275-277(1982)
The techniques allows small molecules such as butane and cyclohexane to be energy minimized into their most stable conformation:

Larger molecules, including DNA and proteins can be modelled using MM software. Below is a representation of bacteriorhodopsin:
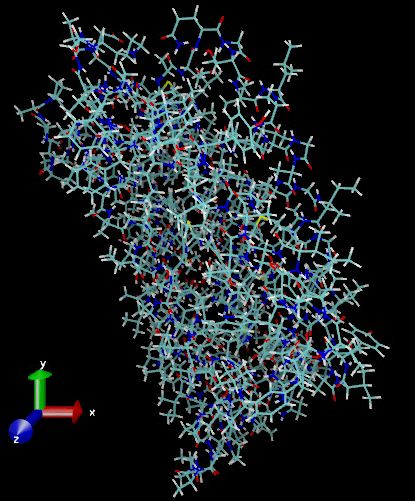
In recent years, molecular mechanics has been extended into molecular dynamics to model large dynamic structures, such as proteins, with move over a given time scale. Have a look here (MM) and here (MD).
Modern Geometry Optimisation Software uses a variety of techniques: molecular mechanics, semi-empirical, ab initio (from the beginning) and density functional. The quantum chemistry software completely hides the mathematics of the geometry optimisation process. A molecule is constructed (drawn) with a mouse and the energy minimized using any desired level of theory.
All computational methods uses a broadly similar strategy. Atoms are placed in virtual space in an approximate geometry with respect to bond lengths and angles. A calculation is performed to determine the energy of the system. The software then alters the geometry, and the energy is recalculated. The software loops, until it finds the arrangement of nuclei which gives the system the lowest energy, and this corresponds to the optimum molecular geometry.
The time taken to minimise depends upon the method used, the size of the molecule, the degree of precision required and well as the processor speed and available memory.
It is possible to mix-and-match. An entire protein may be modelled using MM/MD methodology, with the central active site plus substrate optimised using ab initio techniques. Software is available from a number of vendors: WaveFunction, HyperChem (download a fully functional but time limited demo version) and Gaussian.
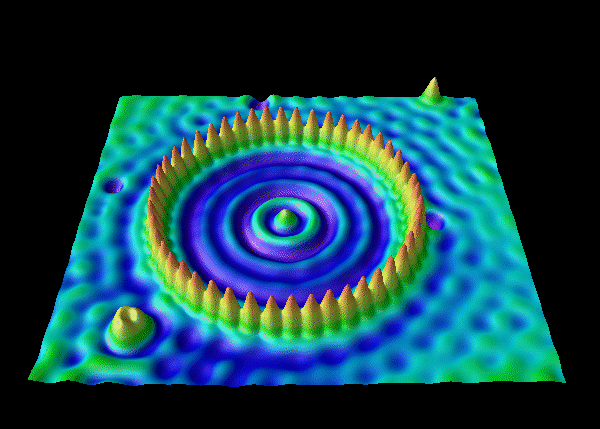
The Electron Corral
The image below is not of an atom, but shows an alternative electron corral pattern, predicted by the Schrödinger wave equation and created by electrons in experiment:
The Bifurcation of Theories & Models
The crucial time for understanding [how we understand] chemical structure & bonding occurred in the active UC Beckley labs of G. N. Lewis over the years from 1912–23.
Lewis and colleagues actively debated the new ideas about atomic structure, the Rutherford & Bohr atoms, and postulated how they might give rise to models of chemical structure, bonding & reactivity. Taken directly from the Bohr atom, the Lewis model uses electrons that are "countable dots of negative charge".
Lewis's first ideas about chemical bonding were published in 1916, and later in a more advanced form in 1923. These early ideas have been extensively developed and are now taught to chemistry students the world over.
More advanced models of chemical structure, bonding & reactivity are based upon the Schrödinger equation in which the electron is treated a resonant standing wave.

Although largely outside the scope of this web book, the theoretical dichotomy also occurs in semiconductor physics where electrical behaviour is either modelled in terms of band theory, a natural development of MO theory or in terms of localized electrons & electron holes within the valance band, a development of the VSEPR model.
Summing Up: Mixing & Matching Models & Theories
Chemical theories are either based on:
Quantum mechanical models that represent electrons as waves. This approach is good at modeling atomic structure, atomic and molecular spectroscopy, the nature of the chemical bond, LCAO, FMO theory and pericyclic chemistry. Mathematical calculations employ Hartree-Fock, density functional or Hückel techniques.
Classical mechanics represents atoms as spheres that bond together and exhibit valency. The geometry of molecules and molecular ions can be very neatly predicted by VSEPR 'theory'. This type of approach can be paramertised into molecular mechanics and molecular dynamics software models.
|
The following is taken from Introduction to Macromolecular Simulation by Peter J. Steinbach:  |
Quantum chemistry texts can blur the distinction between quantum mechanics and classical mechanics and by grouping together LCAO MO calculations along with VSEPR, MM and MD techniques.
Pick n Mix When - as chemists - we consider a substance like ammonia, we employ a variety of models and ideas, fore example:
- Bulk property: Ammonia
is a gas at 20°C 1.0 atm, so it is a molecular substance.
- In VSEPR theory ammonia,
H3N:, has AX3E trigonal
pyramidal geometry: it is a polar molecule with a lone pair of electrons.
- Ammonia is a Lewis base which complexes with the proton to form the ammonium ion, [NH4]+,
and with Lewis acids such as trialkylboranes, R3B.
- The chemistry of ammonia
is dominated by the lone pair of electrons, a model is supported by
the Valence Bond structure.
- FMO theory identifies
the HOMO as being the dominant frontier molecular orbital.
- Quantum chemistry software can be used to calculate the geometry of ammonia, in terms of bond lengths and angles, to high precision. Software can display electron density, HOMO and LUMO surfaces and calculate infrared spectral bands.
Detailed quantum analysis shows that ammonia's trigonal pyramidal structure is able to invert "like an umbrella". In ammonia, this inversion occurs by quantum tunneling.
Can Orbitals be Observed?
One rather important question remains: Do atomic and molecular orbitals exist? Are they real?
The answer is: No. In principle orbitals cannot be observed.
- Orbitals certainly appear to exist, and it is often convenient to talk about them as if they are real, but that is not proof of their actuality.
- Experiments can only measure electron energy and density.
- The wavefunction/orbital |Ψ| gives orbital phase and the squared function, |Ψ|2, gives electron density.
- Thus, orbitals and orbital phase are the square root of the electron density, something that cannot be known the same reason that we cannot know the square root of minus one.
- d-Orbitals project into 5-dimensional space... but our physical universe is only three dimensional.
- It is possible to devise mathematical approaches to molecular structure that do not involve orbitals, for example the Hellmann-Feynman theorem (above) and Heisenberg's matrix mechanics.
- Also:
E. Scerri, Have Orbitals Really Been Observed?, Journal of Chemical Education, 77, 1492-1494, (2000) here.
E. Scerri, The Recently Claimed Observation of Atomic Orbitals and Some Related Philosophical Issues, Philosophy of Science, 68 (Proceedings) S76-S88, N. Koertge, ed. Philosophy of Science Association, East Lansing, MI, (2001), here.
Read More
Introduction to Macromolecular Simulation by Peter J. Steinbach
Theoretical Chemistry a Self-Guided Introduction for College Students by Jack Simons
Read more about Lewis structures and the relationship between Lewis theory and other structural theories in an excellent page by physicist John Denker.
An Introduction to Theoretical Chemistry by Jack Simons
Take a look at: Classic Papers from the History of Chemistry (and Some Physics too)

 |
 |
 |
| Gibb's Build-a-reaction | Modern Lewis Theory |
© Mark R. Leach 1999 –
Queries, Suggestions, Bugs, Errors, Typos...
If you have any:
Queries
Comments
Suggestions
Suggestions for links
Bug, typo or grammatical error reports about this page,please contact Mark R. Leach, the author, using mark@meta-synthesis.com
This free, open access web book is an ongoing project and your input is appreciated.