Periodic Table |
 |
 |
 |
 |
 |
 |
 |
| VSEPR | Polyatomics |
Diatomic Species by Molecular Orbital Theory
Even rather simple molecular orbital (MO) theory can be used to predict which homonuclear diatomic species – H2, N2, O2, etc. – will exist, explain many properties – for example why O2 is a paramagnetic diradical – and identify the important frontier molecular orbitals (FMOs).
Electrons dance to a subtle & beautiful quantum mechanical tune.
The resulting patterns are both complicated & exquisite.
As chemists we try to understand and exploit the dance.
Our physicist friends attempt to understand the music theory.

Quantum Theory
Introduced by Niels Bohr in 1913, the Bohr model is a quantum physics modification of the Rutherford model and is often referred to the Rutherford–Bohr model. (Bohr had conducted post-doctoral research work with Rutherford in Manchester.) The model's key success lay in explaining (correlating) the Rydberg formula for the spectral emission lines of atomic hydrogen, but as a model/theory it was clearly not complete...
Greatly simplifying both the history & the science: In 1916 atomic theory forked or bifurcated into physics and chemistry streams. This divergence continues to this day. |
The physics fork was initiated and developed by Bohr, Pauli, Sommerfield and others. Research involved studying atomic spectroscopy and this lead to the discovery of the four quantum numbers – principal, azimuthal, magnetic & spin – and their selection rules.
A crucial advance was made by De Broglie in 1924 who suggested that the electron could/should be treated as a wave. More advanced models of chemical structure, bonding & reactivity are based upon the Schrödinger equation in which the electron is treated as a resonant standing wave.
Here is a video which presents a map of quantum physics 'the whole thing'. Not all of this video is directly related to chemical structure and bonding, but chemical structure and bonding are quantum mechanical in nature:
AO-AO Interactions
Atomic orbitals, solutions derived from the Schrödingerwave equation, are wavefunctions, where waves are well understood mathematically. Waves can be added together or subtracted from each other.
Consider the addition of two sine waves. The product is a superposition, here:
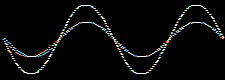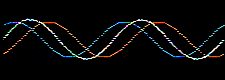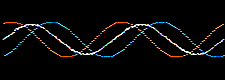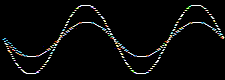
Likewise, atomic orbitals can be added together to give a superposition called a molecular orbital or MO. Molecular orbitals are bonding when the orbital phase considerations are favourable:
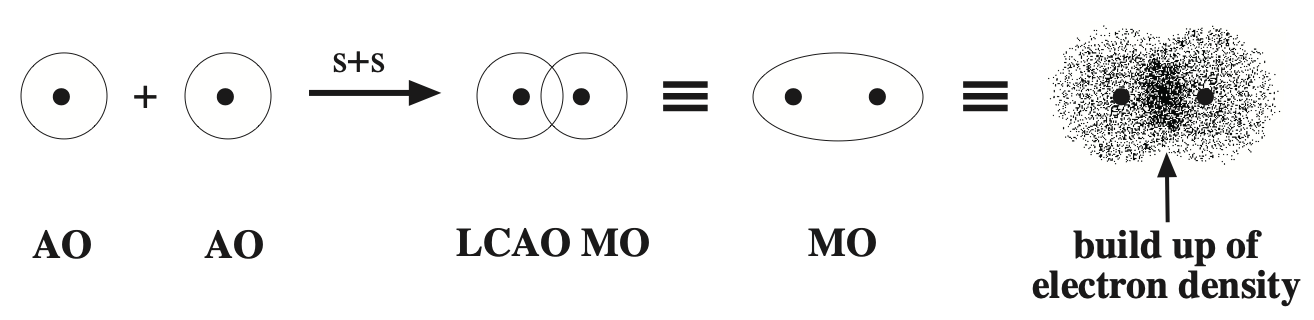
The bonding MO wave function, Ψ (psi), can be squared, |Ψ|2 (psi squared), to represent electron density. A bonding MO shows a build up of electron density between the two positively charged nuclei.
- The two positive nuclei are both attracted to the region of electron density and are shielded from each other.
- This, in essence, is the covalent bond.
* * * * *
A nice physics video by Arvin Ash discussing the formation of the H2 molecule. As far as we are concerned, the interesting analysis is from 2:00 min to 6:40 min:
* * * * *
If the atomic orbitals are "out of phase", the AO/AO interaction will exhibit a phase node – a regions in space with zero electron density – between the positive nuclei. There will be nothing to attract the nuclei together and the MO is (said to be) antibonding:
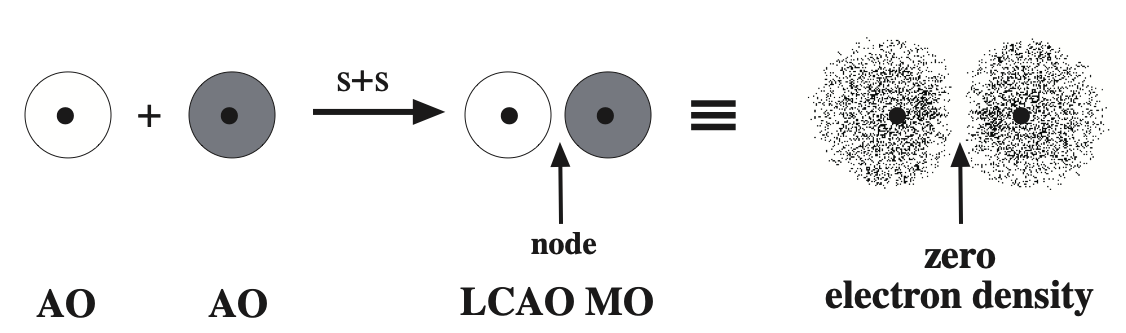
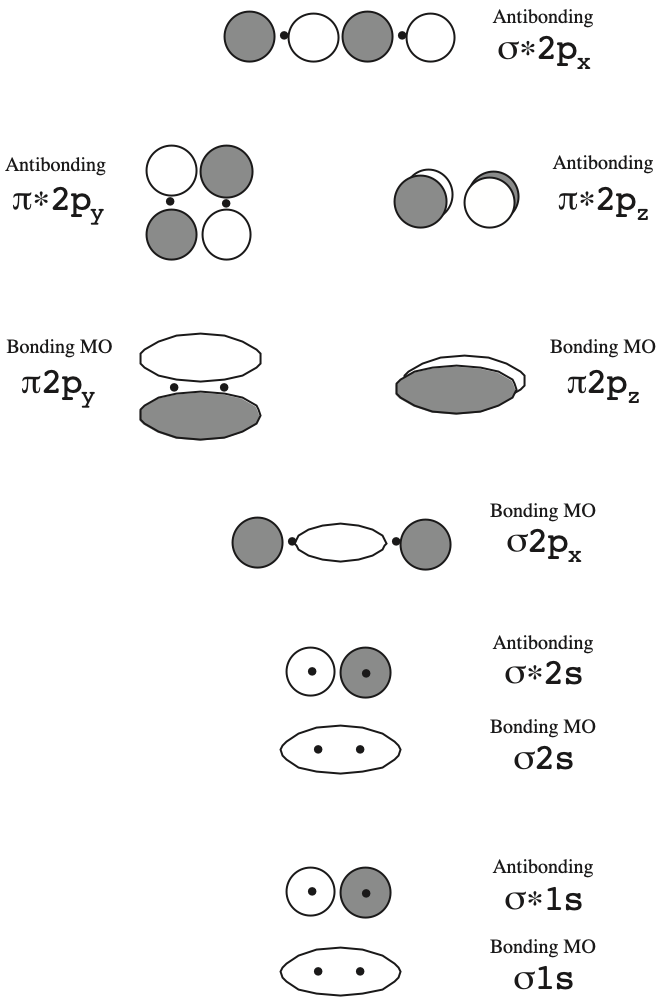
The diagram below shows the atomic orbitals, AOs, on a pair of adjacent atoms interacting with each other.
Note that by convention we start reading from the bottom of the diagram because this is how MO diagrams are constructed, from the lower energies... up.
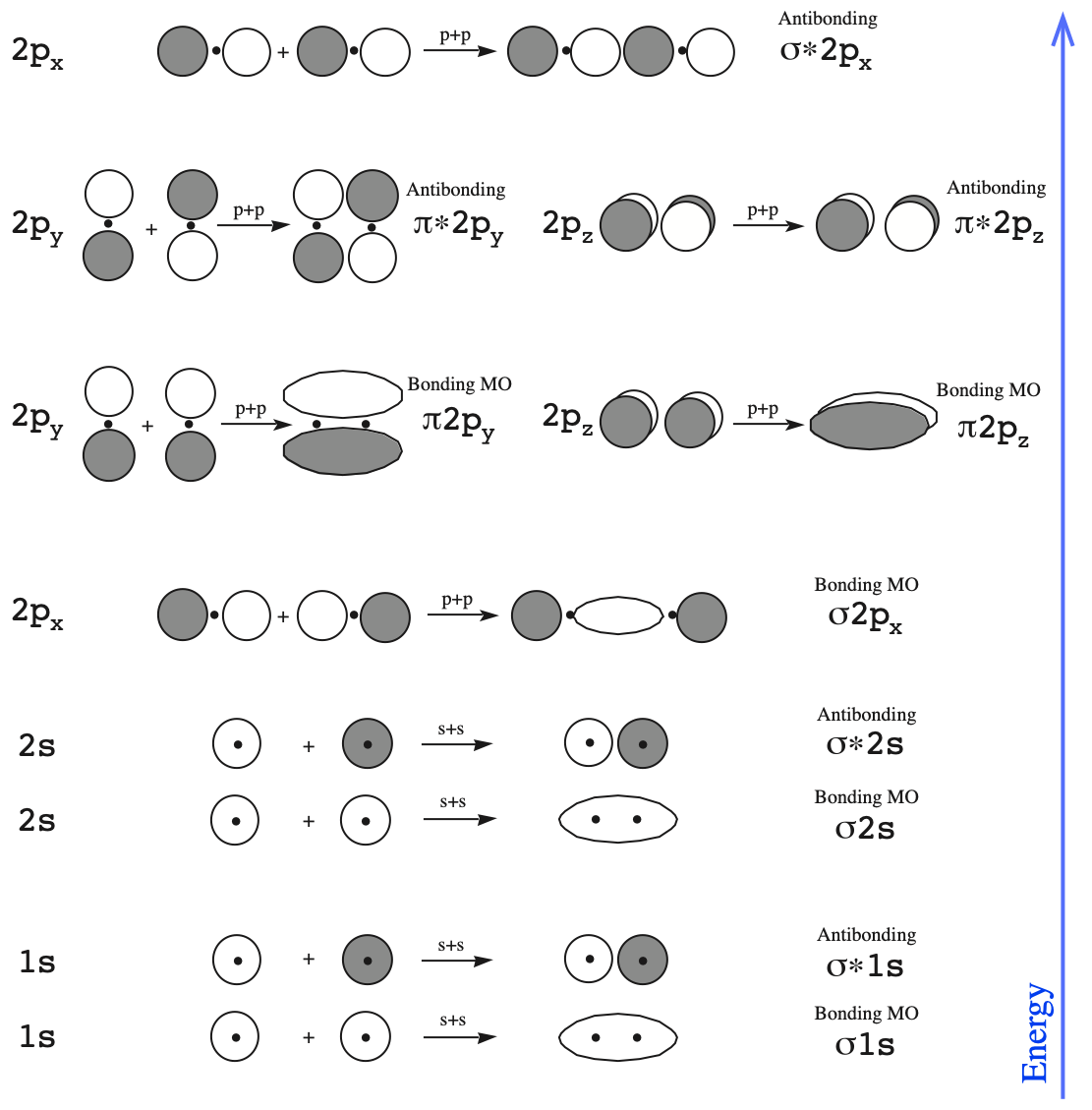
- First, we have the 1s + 1s → sigma bonding MO, and then above this the σ* (sigma star) antibonding MO.
- Then, there are the pair 2s + 2s bonding σ (sigma) and antibonding σ* (sigma star) MOs.
- Next we come to the p + p interactions. These are a little more complicated because p orbitals are orientated in space along the x, y and z dimensions.
- The 2px + 2px orbital interaction gives a σ (sigma) bonding MO.
- The 2py + 2py and 2pz + 2pz interactions are equivalent, they only differ in spatial orientation. Both give rise to π bonding MOs.
- Next come a pair of π* (pi-star) antibonding MOs.
- Finally, we have the 2px + 2px σ* (sigma star) antibonding MO.
The diagram of the bonding and antibonding MOs is shown below:
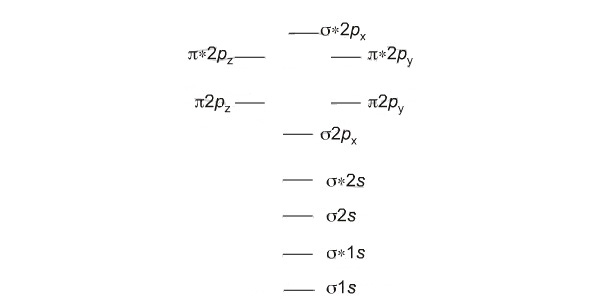
Electrons are added to the MOs (bonding and antibonding) using the same rules that are used for adding electrons to atomic orbitals:
- The aufbau principle, lowest energy MOs fill first, or fill the orbitals from below, if there are large orbital energy differences.
- The Pauli exclusion principle, a maximum of two electrons per orbitals and these must be of opposite spin
- Hund's rule, when there are equal energy or "degenerate" orbitals, these fill one electron at a time before pairing begins. Or, if two orbitals are not very different in energy, near-degenerate, or even exactly degenerate, then two electrons will fill both orbitals with parallel spin.

Leads to:
And so:
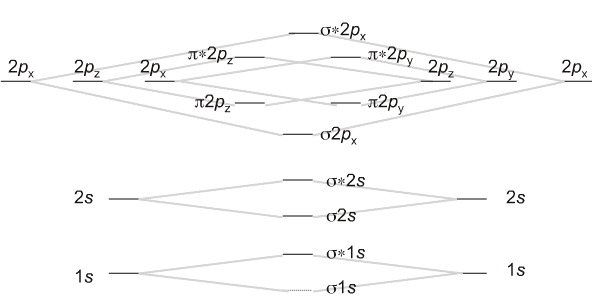
Simple, except that when electrons are added, sometimes the relative energies of the orbitals can change...
Dihydrogen
We can now examine diatomic species. We will start with the interaction of two hydrogen atoms, each with a single electron in a 1s AO.
The two atoms come together and the two electrons go into the σ (sigma) 1s MO with is bonding. H2 is known to exist.

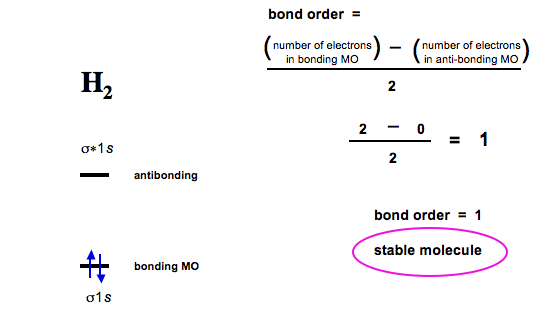
For dihydrogen, H2, we can identify the frontier molecular orbitals (FMOs).
The highest occupied molecular orbital (or HOMO) is the σ (sigma) 1s MO. The lowest unoccupied MO (LUMO) is the σ* (sigma star) 1s MO which is antibonding.
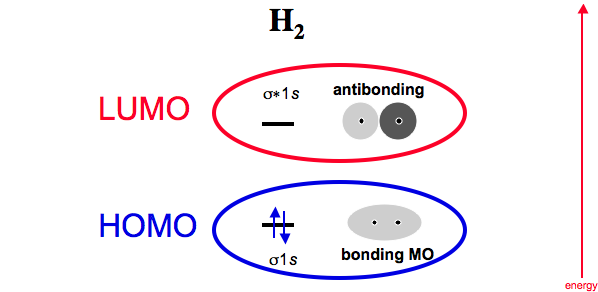
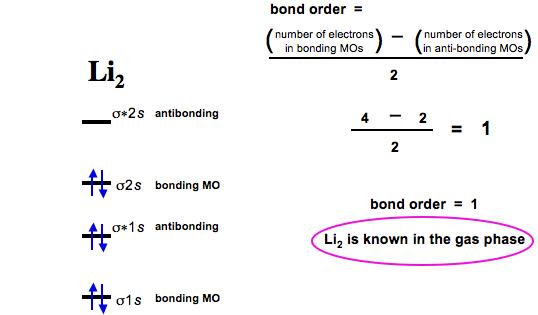
Bond order is defined as the number of electrons in bonding MOs (for H2 this is two) minus the number of electrons in antibonding MOs (zero) divided by two.
Thus, hydrogen has a bond order of 1.
Dihelium
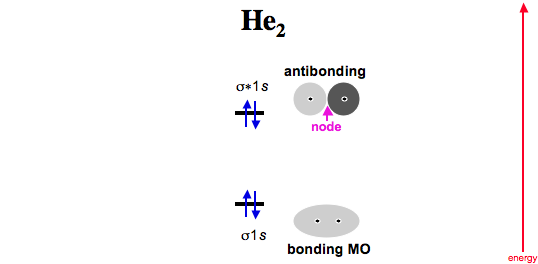
Now consider two helium atoms approaching. Two electrons go into the σ 1s bonding MO, and the next two into the σ* antibonding MO.
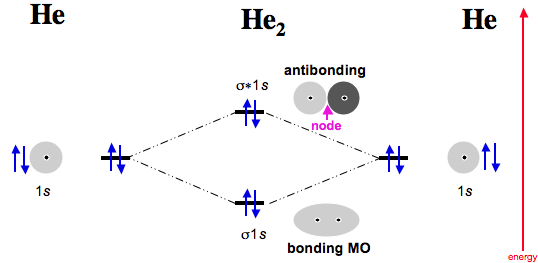
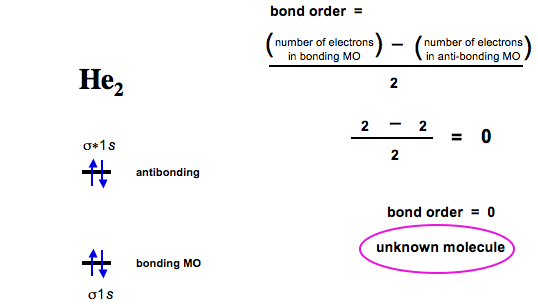
As antibonding MOs are more antibonding than bonding MOs are bonding, He2 (dihelium), is not expected to exist
And dihelium has a bond order of zero and the molecule is unknown:
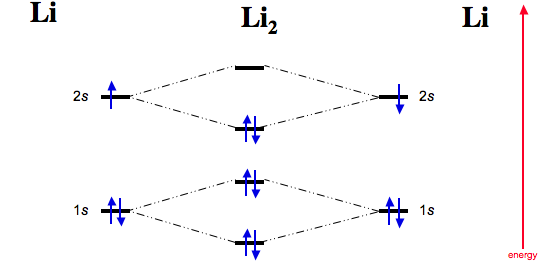
Dilithium
Now consider two lithium atoms interacting.
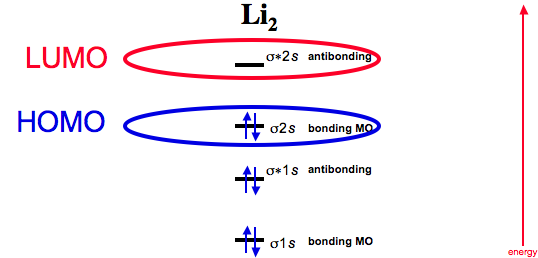
Dilithium, Li2, is known in the gas phase, it has a bond order of one, and it has HOMO + LUMO FMOs:
Note to any trekkies who may have ended up on this page as the result of a google search.
While it may be possible to prepare dilithium crystals, they will not be a viable energy source capable of powering a Starship to warp speed...
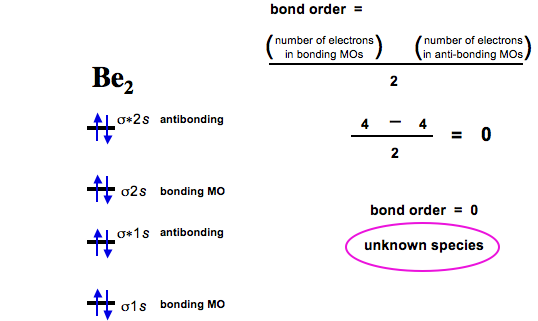
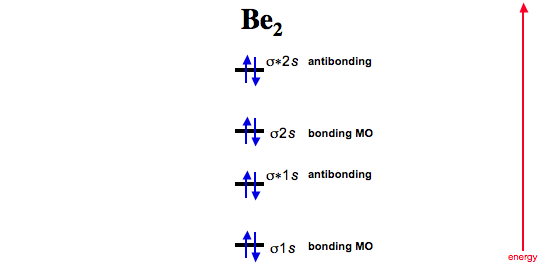
Diberyllium
Now consider two beryllium atoms interacting. Diberyllium, Be2, has a bond order of zero and is unknown:

Quantum Patterns
Quantum mechanics is all about patterns. The problem is that just when we think we are starting to understand the patterns... Mother Nature shows that she has other ideas...
On going Li2, B2, C2, N2, O2, F2, Ne2 the complexity of the molecular orbitals develop in two ways:
- The p-orbitals can interact with each other end on to give σ-bonding and σ-antibonding molecular orbitals OR they can interact side-ways on to give π-bonding and π-antibonding molecular orbitals that come in degenerate (equal energy) pairs. Electrons continue to be added according to aufbau, Pauli & Hund.
- As the electrons are added the relative energies of the orbitals changes.
First we see how the energy of 3σg MO drops below the 1πu MO of going from N2 to O2. (Note that σ and π bonding MOs are coloured black and the σ• and π• antibonding MOs are brown):
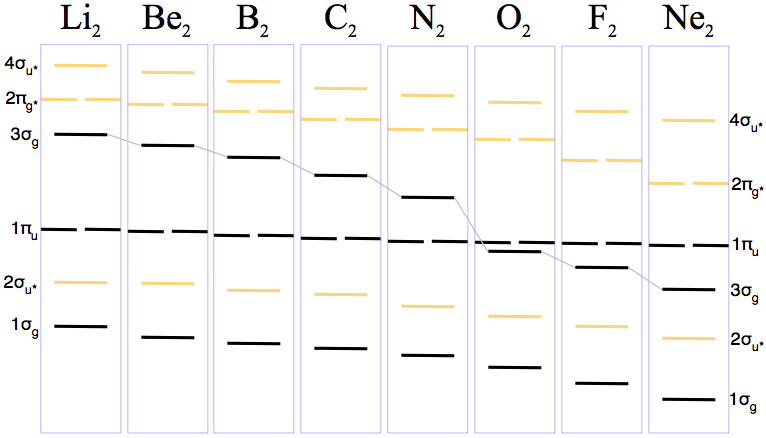
Next the electrons are added according to the aufbau (build-up) principle, the Pauli exclusion principle & Hund's rule.
This analysis gives rise to some very common species (N2, O2 & F2), some rare species (B2 & C2) and some unknown species (Be2 & Ne2). Indeed, existence can be predicted by bond-order in that the bond-order = 0 species are unknown:

Note:
- Bond order > 0 are all known, although not necessarily
as room temperature stable diatomic materials. Lithium, boron and carbon
diatomic 'polymerise' to metals or network
covalent materials.
- Dicarbon is VERY
reactive and it will polymerise (depending upon the conditions) to diamond, graphite, C60 buckyballs and similar
species, single walled carbon nanotubes (SWNT) and multi walled carbon
nanotubes.
- The orbital shapes can be calculated using MO software, such as Spartan by Wavefunction:
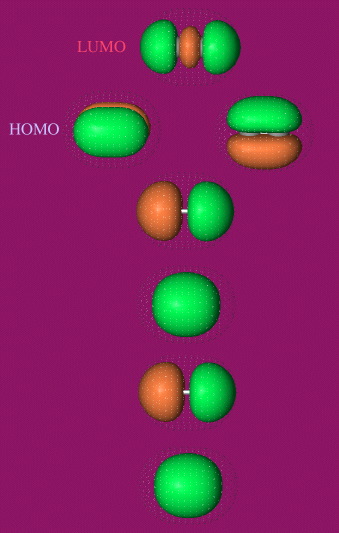
Calculated at the HF 6-31G* level.
- The diradical nature of triplet oxygen causes it to be paramagnetic. Read more about diradicals, including triplet and singlet oxygen, elsewhere in this webbook.

- The data can be summarized:
Diatomic |
Bond Order |
FMOs |
H2 |
1 |
HOMO + LUMO |
He2 |
0 |
Unknown Species |
Li2 |
1 |
HOMO + LUMO |
Be2 |
0 |
Unknown Species |
B2 |
1 |
Diradical |
C2 |
2 |
HOMO + LUMO |
N2 |
3 |
HOMO + LUMO |
O2 |
2 |
Diradical
|
F2 |
1 |
HOMO + LUMO |
Ne2 |
0 |
Unknown Species |
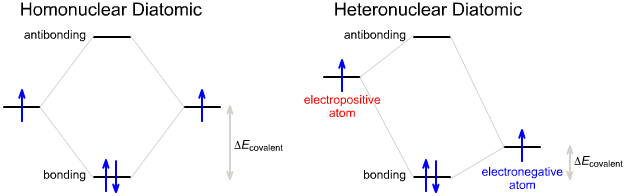
Heteronuclear Diatomic Molecules & Molecular Ions
MO theory can be used to describe heteronuclear diatomic molecules & molecular Ions such as:
- LiH Lithium hydride
- HF Hydrogen fluoride
- CO Carbon monoxide
- CN– Cyanide ion
- NO+ Nitrosonium ion
As the electronegativity differences increases the interacting orbitals will be at different energies. The result is that the covalent bonding energy decreases, but this is counteracted by an increasing electrostatic +/– attraction that is not represented on MO diagrams (see the Klopman equation, elsewhere in this web book.)
The MO diagram for the diatomic carbon monoxide, CO, shows it to be isoelectronic with nitrogen, N2:
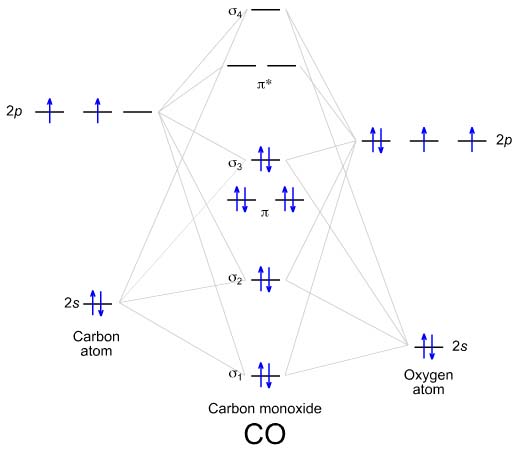
The heteronuclear diatomic ions cyanide ion, CN–, and nitrosonium ion, NO+, are also electronic with nitrogen, N2, and carbon monoxide. The only difference between the MO diagrams are the relative energies of the orbitals.
Please note that the primary aim of this page has been produced to introduce the idea of molecular orbitals and to show that the stable homonuclear diatomic species possess either LUMO and HOMO frontier molecular orbitals, or are diradical species.
The following is a message from Dr Eugen Schwarz in Germany – for which I am most grateful – concerns the above analysis:
|
Hi Mark, Non-overlapping core AOs should not be split into bonding and antibonding MOs, since there are (localized or delocalized) quasi-degenerate and non-bonding, in accordance with photoelectron spectroscopy, PES. You correctly mention that 1s-1s is strongly antibonding, but the sigma-g/u splitting is symmetric in the diagrams. Also there is 2s-2p mixing, therefore 2s-2s is not more, but less, antibonding than 2s+2s is bonding: 2s-2s is nearly non-bonding, and Be2 is a very weakly bound molecule. Similarly 2p+2p is only weakly bonding, and in N2 it is just non-bonding. Spins are vectors in space, which are never vertical. The spin-z axis angle is the magic one, about 55 deg., So there is an angle between so-called parallel spins of about 70 deg. Antiparallel spins are exactly antiparallel. alpha * beta for two electrons means both antiparallel or pseudo-parallel. In AO level diagrams, it is important to note the large differences of gaps:
But correctly, according to both spectroscopy and quantum chemistry:
Note the d < s order given here, which is the correct one for most cases, with the exception of group 1 and 2 atoms. It is order of orbitals and gaps, that explains the lengths of the rows of the periodic table:
Eugen Schwarz |
For more information, look here.
And, from Eric Scerri a video discussing the nature on the covalent bond at a deeper level than discussed above:
 |
 |
 |
| VSEPR | Polyatomics |
© Mark R. Leach 1999 –
Queries, Suggestions, Bugs, Errors, Typos...
If you have any:
Queries
Comments
Suggestions
Suggestions for links
Bug, typo or grammatical error reports about this page,please contact Mark R. Leach, the author, using mark@meta-synthesis.com
This free, open access web book is an ongoing project and your input is appreciated.