Periodic Table |
 |
 |
 |
 |
 |
 |
 |
| Segrè Chart | What is the Periodic Table Showing? |
Quantum
Numbers to Periodic Tables:
The Electronic Structure of Atoms
A Google image search on the term "atom" will usually produce two general types of picture showing the Rutherford atom of 1911 or the Bohr atom of 1913:

Unfortunately, both of these conventional representations are incorrect (in several ways), and the electronic structure of atoms needs to be understood in terms of the quantum mechanical Schrödinger wave equation... and the nucleus is tiny (but very, very dense).
Atoms
In stars atomic nuclei are born naked, but their net positive charge, equal to their atomic number Z, attracts the comparatively mass-less electrons to produce neutral atoms.
The nucleus of a gold atom has an atomic of atomic number, Z = 79, so the Au79+ ion attracts 79 negatively charged electrons to give a neutral atom of gold, Au.
The first problem with the atom images shown above is that the atomic nucleus is absolutely tiny compared with the size of the overall atom, as shown by the famous Rutherford experiment which involved 'firing' alpha particles through gold leaf.
Compared with the size of the gold nucleus, a gold atom is huge... comparable with the relative size of the Sun and solar system. From HyperPhysics, but converted to metric units:

So the atom structure diagrams should be modified to show a tiny point like nucleus:

The Electronic Structure of The Atom
The second problem with the conventional images above is that the negatively charged electrons "associate" with the positively charged nucleus as three dimensional resonant standing waves:
The electrons move about the point positive charge
in a beautiful & subtle quantum mechanical dance
The modes of resonance for single electron systems such as the hydrogen atom are described by the Schrödinger wave equation.
Very, very briefly Schrödinger knew of de Broglie's proposal that a moving particle has wavelength, l, proportional to Planck's constant, h, and 'one over' momentum p, so that l = h/p, a property we now known as wave-particle duality.
Schrödinger constructed a differential equation for a wave-like electron resonating in three dimensions about a point positive charge. This is the time-independent Schrödinger wave equation. (Wikipedia):
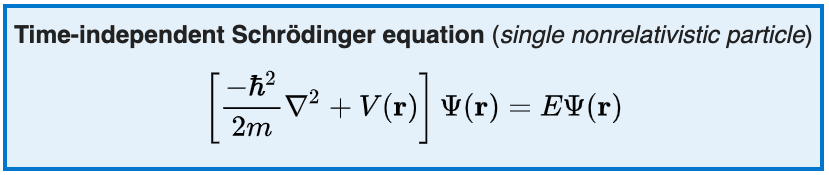
- Solutions to the
Schrödinger wave equation correspond to modes of electron resonance
and are formally called wavefunctions.
- The quantised wavefunctions and the corresponding energy levels correspond to the energy levels in one electron atoms & ions: H•,
He+, Li2+, Be3+, etc.
- The energy difference between these energy levels result in the spectral lines of these species.
- Although not exactly
the same, chemists tend to call wavefunctions "orbitals".
[Thanks to Mark Kubinec Director, Digital Chemistry Project, UC Berkeley for a suggested rewording of these bullet points and suggested that some of the videos from UC Berkeley may be of interest.]
1-Dimensional resonant standing waves: the vibrating string:
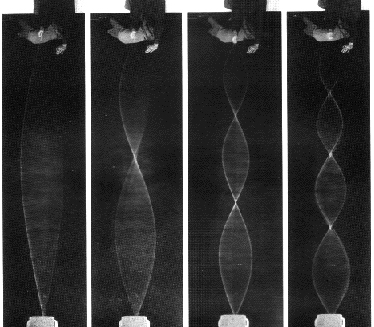
2-Dimensional resonant standing wave, a vibrating drum skin:

and a square plate:
3-Dimensional resonant standing waves:
and a sphere:
Quantum Numbers to Orbitals
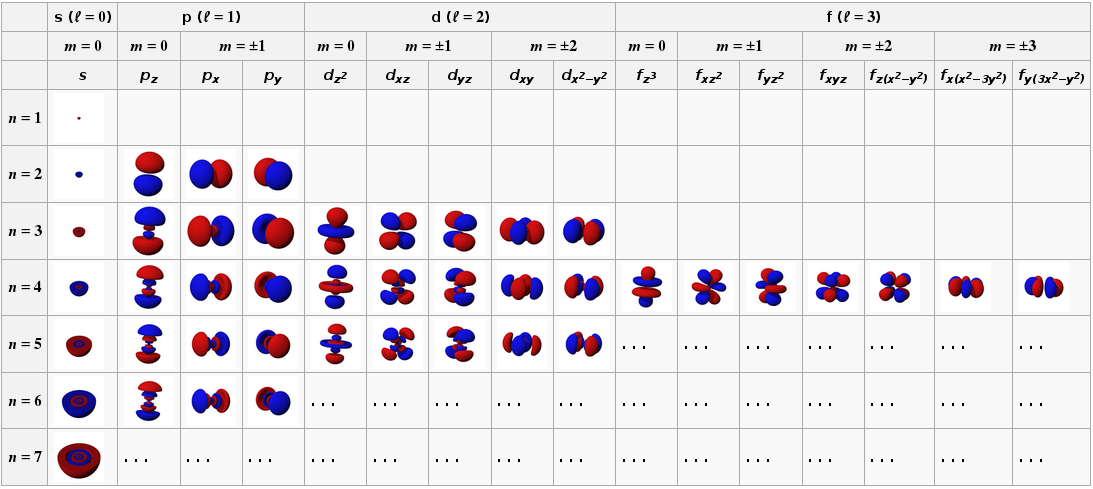
Chemists recognise s, p, d & f atomic orbitals. Their topologies (shape, phase) and electron occupancy are described by four quantum numbers:
n |
The principal quantum number |
ℓ |
The subsidiary or azimuthal or angular momentum or orbital shape quantum number |
mℓ |
The magnetic quantum number |
ms |
The electron spin quantum number |
From Wikipedia:

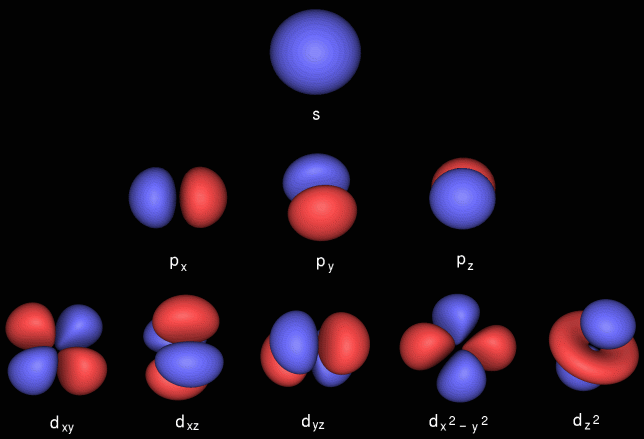
These quantum numbers conspire to give spherical s-orbitals, dumbbell shaped p-orbitals that come in sets of three, double dumbbell d-orbitals that come in sets of five, etc.
Electrons enter and fill orbitals according to four rules*:
|
Pauli
Exclusion Principle
|
Orbitals can contain a maximum of two electrons which must be of opposite spin. |
|
Aufbau or Build-up Principle
|
Electrons enter and fill lower energy orbitals before higher energy orbitals. |
|
Hund's
Rule
|
When there there are degenerate (equal energy) orbitals available, electrons will enter the orbitals one-at-a-time to maximise degeneracy, and only when all the orbitals are half filled will pairing-up occur. This is the rule of maximum multiplicity. |
|
Madelung's
Rule
|
Orbitals fill with electrons as n + ℓ, where n is the principal quantum number and ℓ is the subsidiary quantum number. This rule 'explains' why the 4s orbital has a lower energy than the 3d orbital, and it gives the periodic table its characteristic appearance. |
*However, however, however...
- There are actually more considerations than these simple 'four rules' might suggest, particularly for heavier elements. It is actually necessary to take into account many subtleties with respect to: nuclear screening, electron repulsion, spin-orbit coupling, electron exchange energies, relativistic effects, etc. The greater the number of electrons the more considerations there are. Whereas one electron atoms and ions: H•,
He+, Li2+, Be3+, etc. can have their electronic structure calculated (solved, deduced) analytically, this is not the case with multi-electron systems.
- For the lighter elements – up to Z ~ 50 – the above ml & ms analysis for atomic orbitals (AOs) is fine, but for heavier elements it is necessary to consider spin-orbit coupling, not only in atomic spectroscopy of the elements but also in their reaction chemistry.
- Madelung's rule is very much a "rule of thumb" and has many exceptions. Indeed, it only works for two thirds of the transition elements.
- Transition metal chemists know that electrons fill orbitals according to increasing energy – the aufbau principle – provided that the energy gap, Δε, is larger than the orbital-orbital exchange energy correction.
- etc.
Many thanks to W. H. Eugen Schwarz for the above comments. Read more in Dr. Schwarz's papers:
- Physical origin of chemical periodicities in the system of elements (open access)
- Measuring Orbitals: Provocation or Reality?
Eric Scerri has suggested that the aufbau principle & Madelung's rule have so many anomalies that they should be taught with the anomalies; they are so numerous they cannot be simply ignored:
Some of these matters are discussed in this video by the author of this web book:
* * * * *
That said, certain magic numbers of electrons about an atomic nucleus exhibit "full shell" stability: 2, 10, 18, 36, 54 & 86. These are associated with the Group 18 inert or noble gases: He, Ne, Ar, Kr, Xe & Rn and their corresponding isoelectronic ions:
2 electrons: H–, He, Li+, Be2+
10 electrons: N3–, O2–, F–, Ne, Na+, Mg2+
18 electrons: P3–, S2–, Cl–, Ar, K+, Ca2+, Sc3+, Ti4+
36 electrons: As3–, Se2–, Br–, Kr, Rb+, Sr2+, Y3+
54 electrons: Sb3–, Te2–, I–, Xe, Cs+, Ba2+, Lu3+
A great deal of main group and organic chemistry can be considered in terms of atoms and ions behaving so as to obtain stable 'full shell' [Group 18 element like] electronic configurations.
Electron Spin
As chemists we say (as above) "an orbital can contain a maximum of two electrons, and these must be of opposite spin". This raises the question: "What exactly is spin?"
The following physics video starts to answer the question, but note the opening line: "Quantum mechanics has lots of weird stuff, but there is one thing that everyone agrees... no one understands quantum spin..."
If you require an even deeper dive into quantum spin, these two linked videos by Physics Explained will be of huge interest. The videos discuss the history and the mathematics.
The videos show that the Dirac formulation of the relativistic electron inevitably has four answers or solutions:
- Spin-up electron
- Spin-down electron
- Spin-up positron (anti-electron)
- Spin-down positron
- The result also shows that the spin must be +1/2 or –1/2.
I can just about follow the logic of the maths (I take on trust the steps shown are correct).
Quantum Patterns
The pattern of orbital structure is very rich and can be mapped onto the two dimensions of paper in many different ways.
Some mappings emphasize how the orbitals are ordered and filled with electrons, others stress how the chemical elements and their orbitals are ordered with respect to atomic number Z. Each tells us something different about atomic orbital structure and/or elemental periodicity.
However, please be aware that the representations shown below are idealised and that Madelung's rule is a 'rule of thumb' rather than hard science.
Orbital Filling
Madelung's Rule says the orbitals fill in the order n + l (lowest n first), giving the following sequence:
(n = 1) + (l = 0) = 1 1s
(n = 2) + (l = 0) = 2 2s
(n = 2) + (l = 1) = 3 2p
(n = 3) + (l = 0) = 3 3s
(n = 3) + (l = 1) = 4 3p
(n = 4) + (l = 0) = 4 4s
(n = 3) + (l = 2) = 5 3d
(n = 4) + (l = 1) = 5 4p
(n = 5) + (l = 0) = 5 5s
and so on...
The sequence can be visualised with the following diagram:
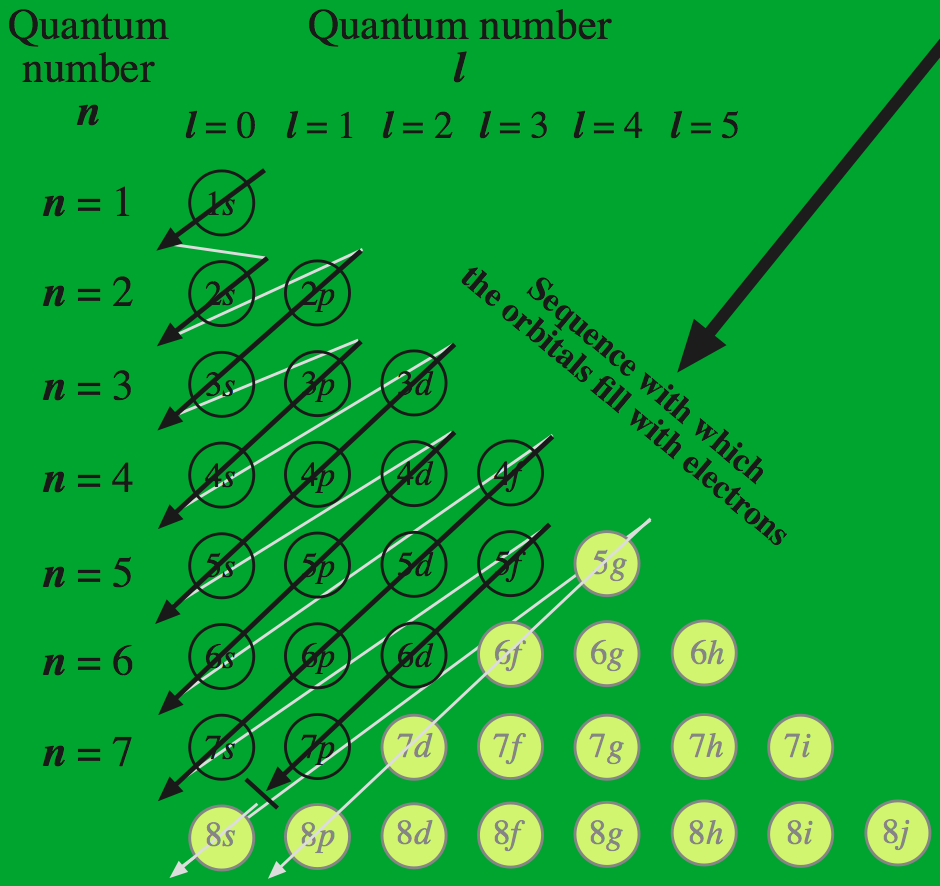
Thus, the afbau principle of orbital filling sequence is, from the bottom of this diagram, upwards because the lowest energies fill first:
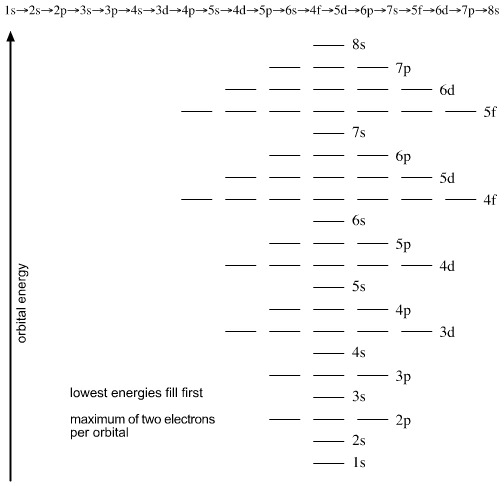
Electron Shells
As electrons are added, the quantum numbers build up the orbitals. Read this diagram, from the top downwards:


Elements by Orbital
The electronic structure can be illustrated adding electrons to boxes (to represent orbitals). This representation shows the Pauli exclusion principle, the aufbau principle and Hund's rule in action.
There are some subtle effects with the d-block elements chromium, Cr, and copper, Cu:
Chromium has the ground state formulation: [Ar] 3d5 4s1 and not: [Ar] 3d4 4s2
Copper has the ground state formulation: [Ar] 3d10 4s1 and not: [Ar] 3d9 4s2
What Do Atoms Look Like? Atoms Are Fuzzy
The video below shows how electrons and orbitals add to 'make' the first few elements of the periodic table:
One of several animations and explanations/realisations of quantum physics from Data-Burger, scientific advisor: J. Bobroff.
What is particularly nice about this video is that it shows a quantum fuzziness: the atoms are not smooth balls.
This explains/shows how and why induced-dipole/induced-dipole (London force) interactions occur between atoms and molecules, an important class of intermolecular interaction/attraction.
- At any moment, the electron distribution around an atom is not perfectly spherical, which means that there is an "instantaneous dipole" on the atom, either δ+ or δ–.
- This instantaneous dipole is able to induce [polarise] a dipole on an adjacent atom, with the effect that the two atoms are attracted to each other, when they are very close or touch. The overall effect is that atoms have a sticky surface, a bit like Velcro.
This effect explains why the Group 18 noble gas elements are able to condense into liquids & solids at low temperature at low temperatures. Likewise, for non-polar molecules, such as: Cl2, Br2, I2, P4, S8, hydrocarbons, etc.
Another video representation, this time by minutephysics:

These representations are way cool and far better than the two diagrams at the top of the page, but there are a couple of things that I, personally, do not like about the minutephysics representation.
- Orbital phase is not shown.
- All of the atoms shown are excited states of the hydrogen atom, and not elements of the periodic table. I do realize that this is for clarity... and the video is made by a physicist and not a chemist!
The Periodic Table
A [periodic] table – of sorts – can be constructed by listing the elements by n and l quantum number:
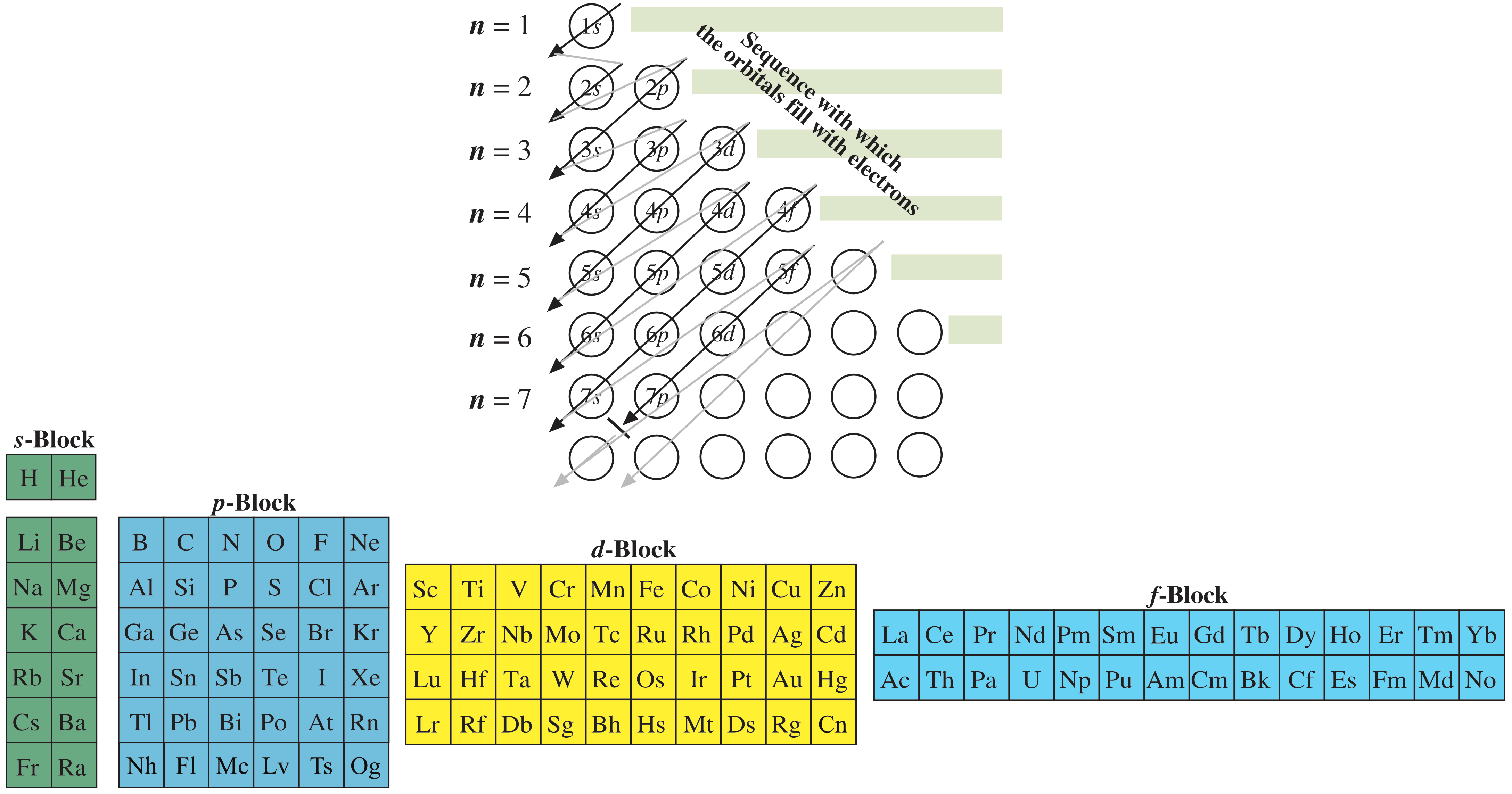
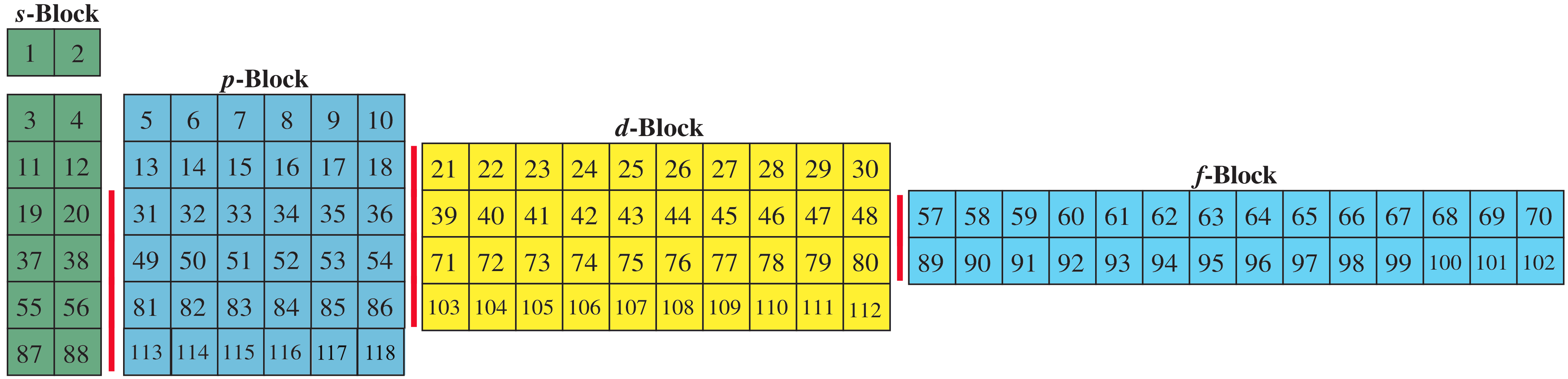
The problem with this mapping is that the generated sequence is not contiguous with respect to atomic number atomic number, Z, and so is NOT a periodic table. Try counting the numbers past the red lines | on this representation:
Named after a French chemist who first published in the formulation in 1929, the Janet or Left-Step Periodic Table uses a slightly different mapping that is contiguous with atomic number:
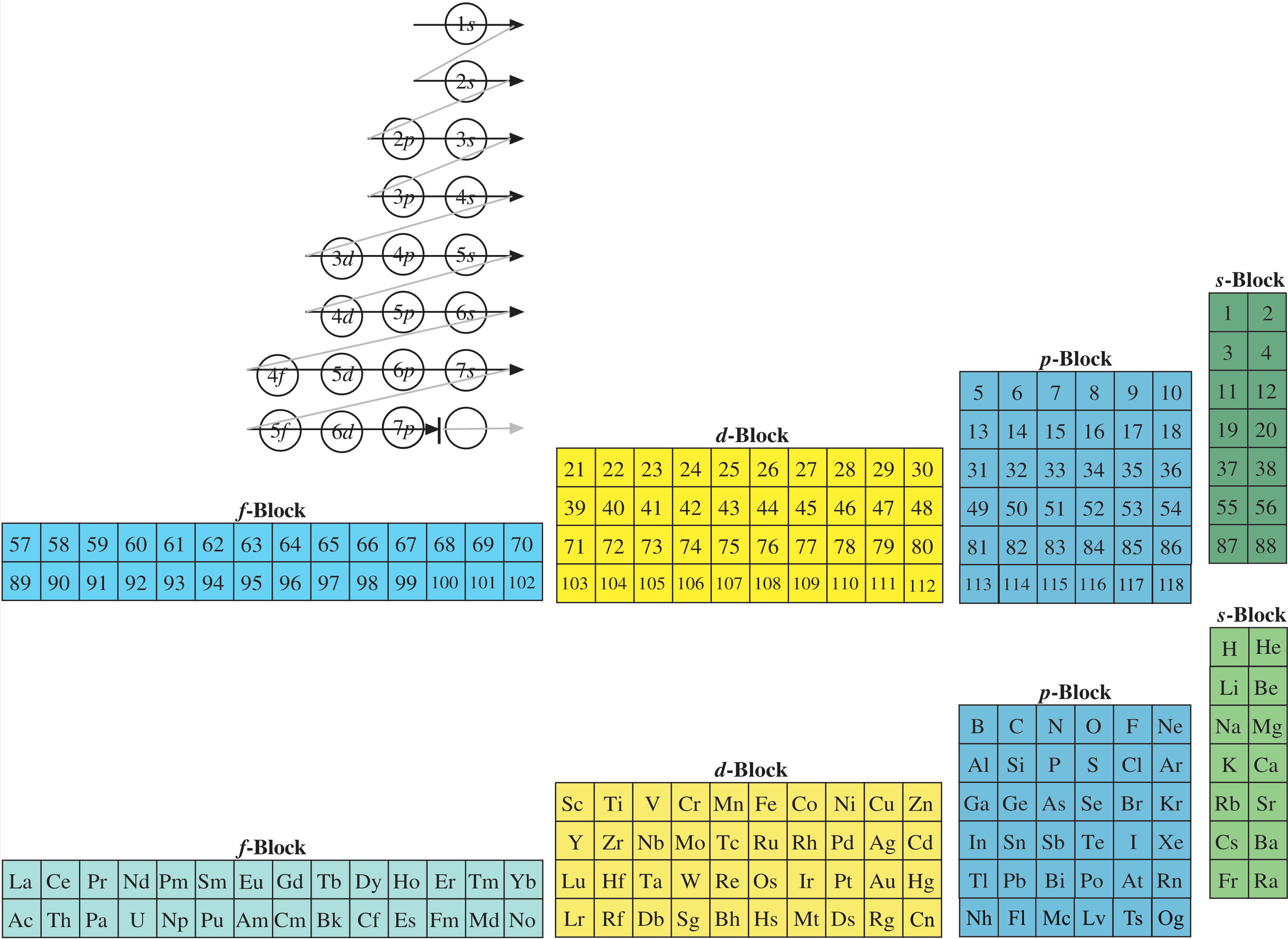
While the Janet periodic table is very logical and clear, it does not separate metals from non-metals as well as the Mendeleev version, and helium is problem chemically.
However, it is a simple 'mapping' to go from the Janet or Left-Step periodic table to a modern (Seaborg) formulation of Mendeleev's periodic table.
There are a couple of steps:
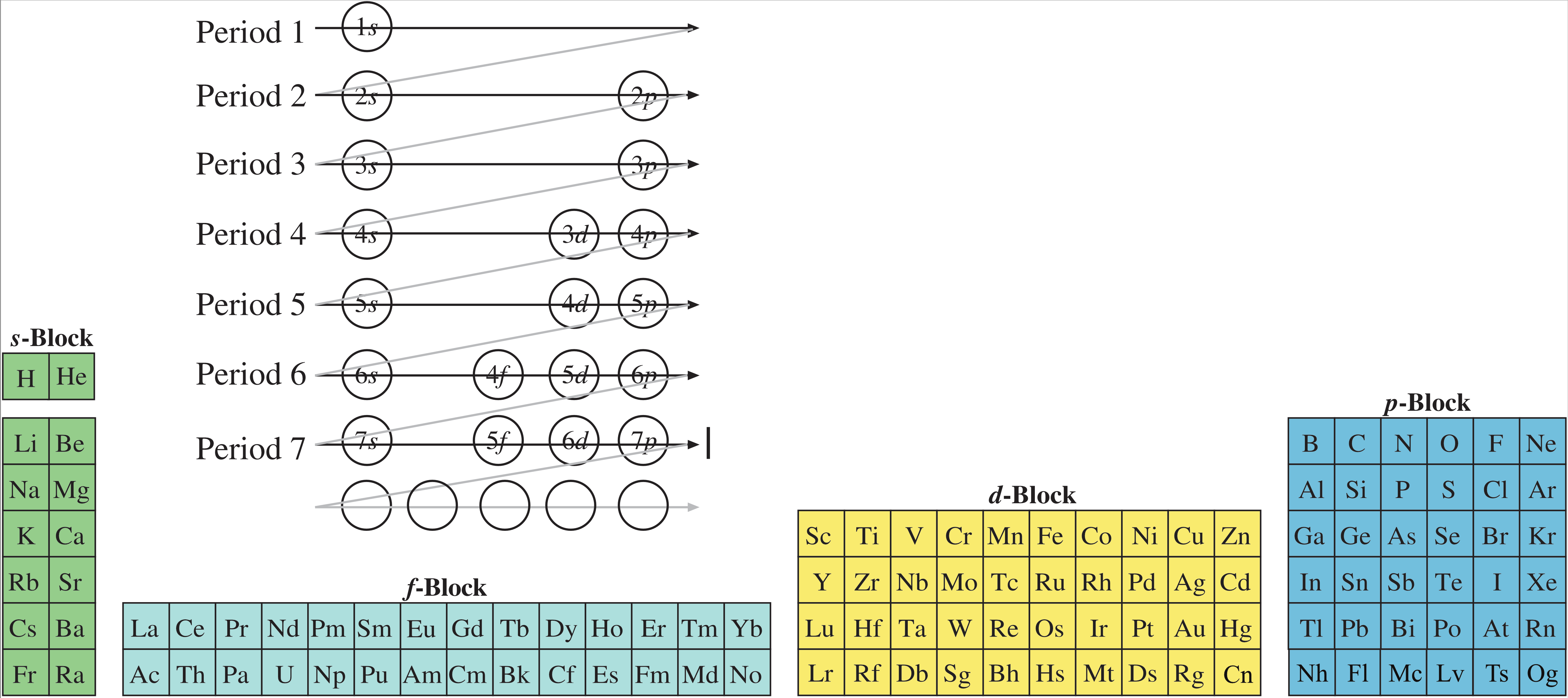
Including the movement of He to Group 18:
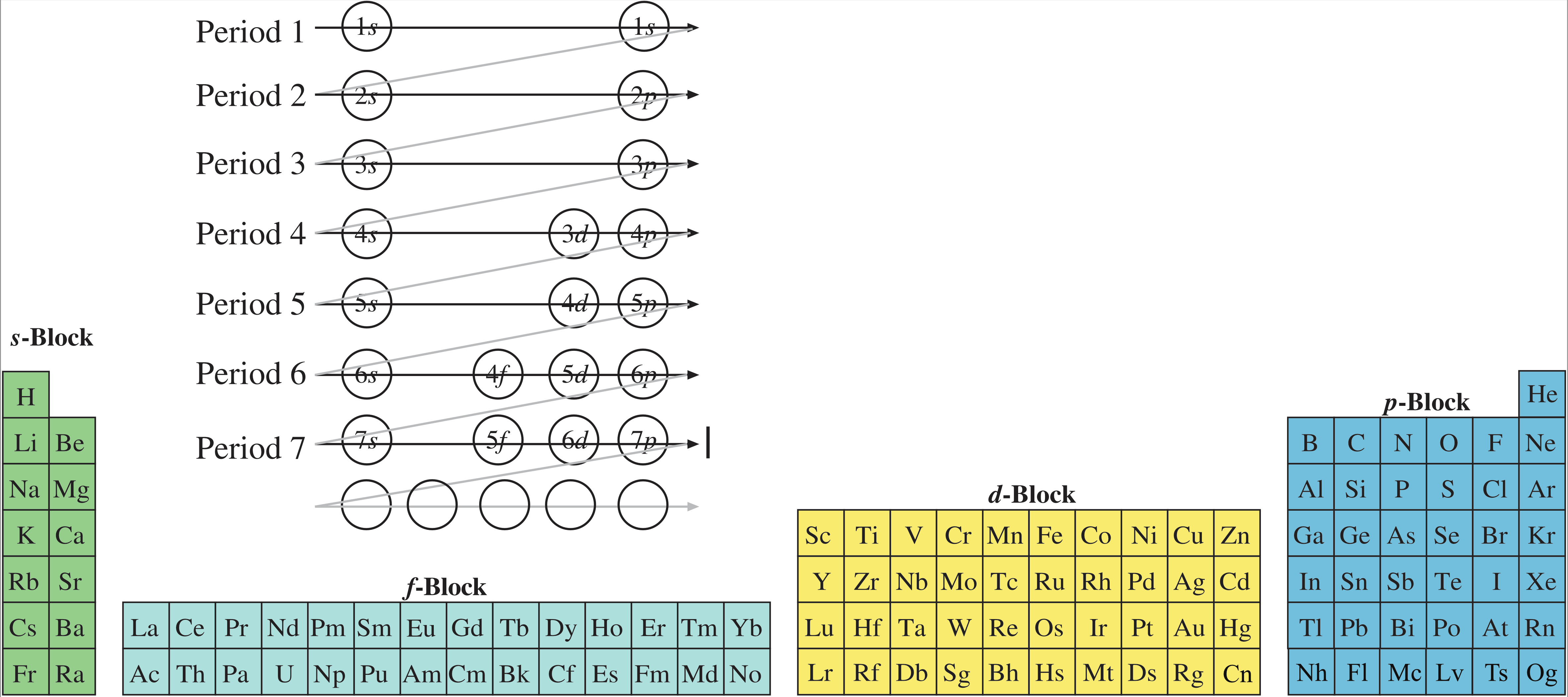
Drop the f-block down, and move the s-block and d and p-blocks into the space produced, and this gives the commonly used medium form periodic table:
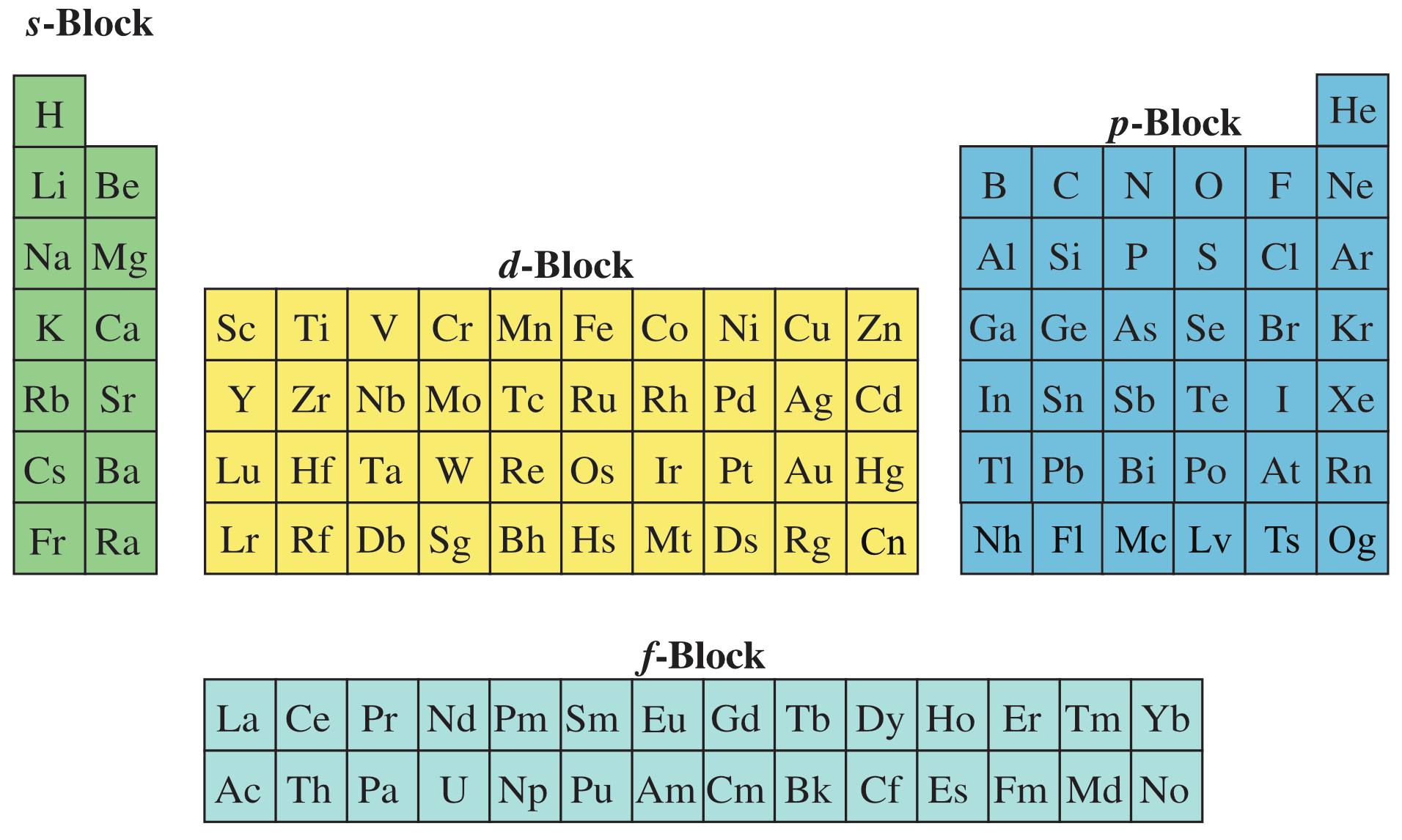
Note, this is the more 'correct' medium form, with Group 3 as: Sc, Y, Lu & Lr and with the f-block as La-Yb and Ac-No.
Many medium form periodic tables incorrectly [in this author's opinion] leave a gap where Lu and Lr are situated, and then add these two elements to the end of the f-block:
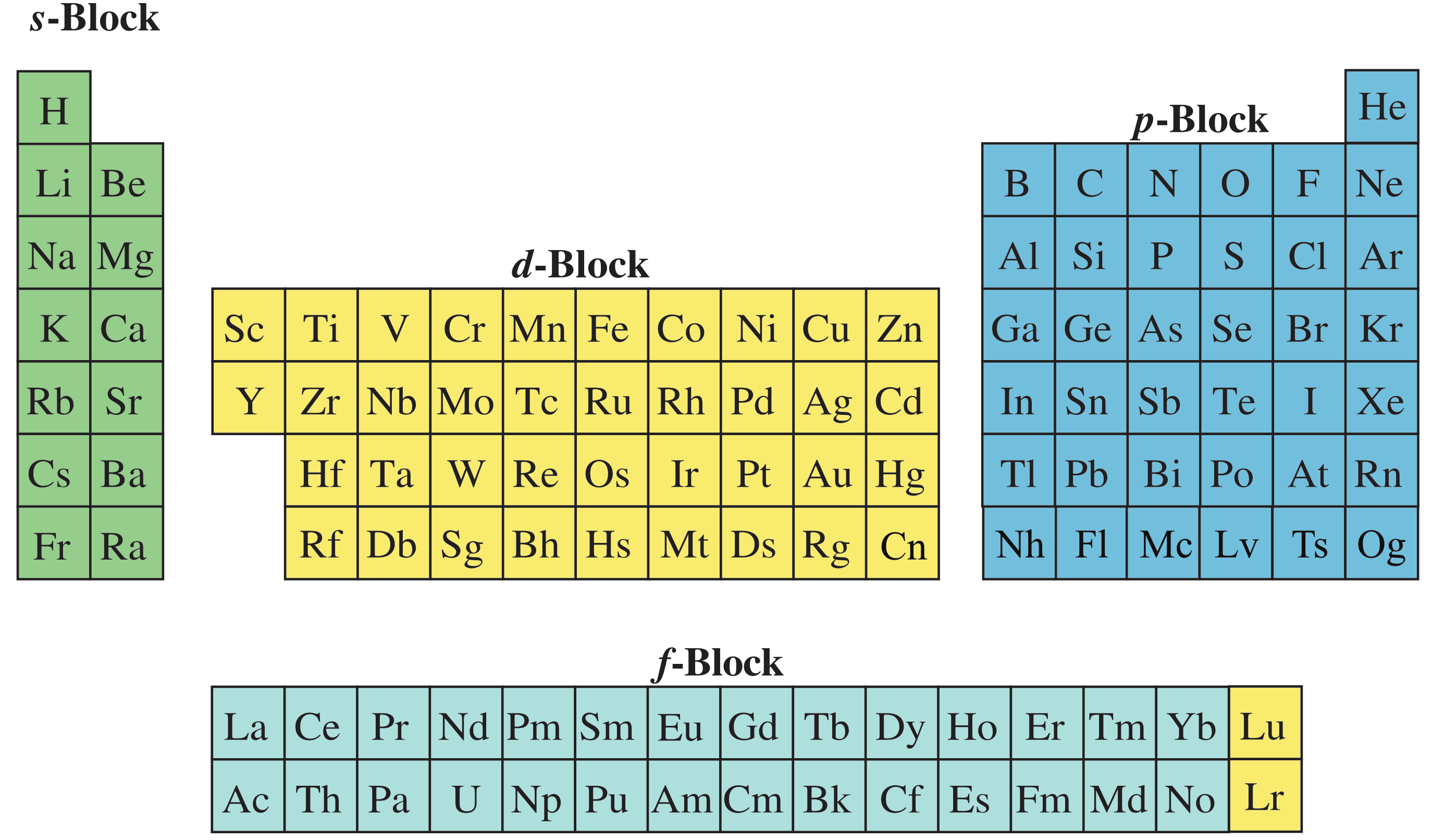
 |
 |
 |
| Segrè Chart | What is the Periodic Table Showing? |
© Mark R. Leach 1999-
Queries, Suggestions, Bugs, Errors, Typos...
If you have any:
Queries
Comments
Suggestions
Suggestions for links
Bug, typo or grammatical error reports about this page,please contact Mark R. Leach, the author, using mark@meta-synthesis.com
This free, open access web book is an ongoing project and your input is appreciated.