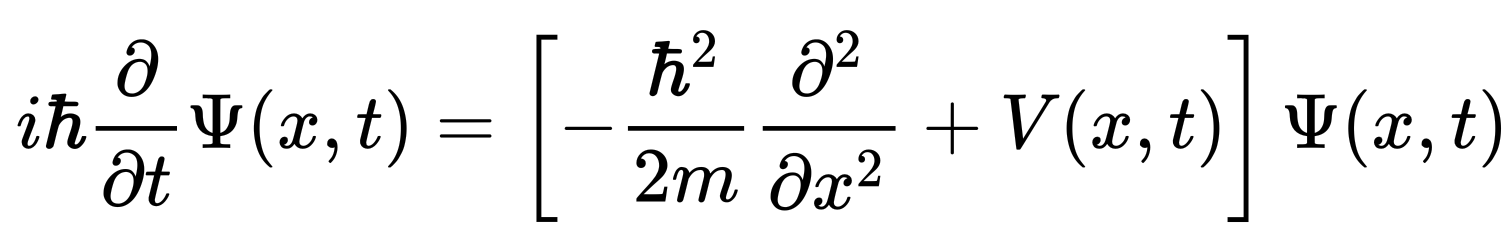Periodic Table |
 |
 |
 |
 |
 |
 |
 |
| What is the Periodic Table Showing? | Periodicity |
The INTERNET Database of Periodic Tables
There are thousands of periodic tables in web space, but this is the only comprehensive database of periodic tables & periodic system formulations. If you know of an interesting periodic table that is missing, please contact the database curator: Mark R. Leach Ph.D. The database holds information on periodic tables, the discovery of the elements, the elucidation of atomic weights and the discovery of atomic structure (and much, much more).
The 10 most recent entries to the database:
| Year: 1932 | PT id = 1379, Type = structure |
Chadwick and the Discovery of the Neutron
Chadwick, J. Possible Existence of a Neutron. Nature, 129, 312 (1932).
"James Chadwick was a British experimental physicist who received the Nobel Prize in Physics in 1935 for his discovery of the neutron. In 1941, he wrote the final draft of the MAUD Report, which inspired the U.S. government to begin serious atomic bomb research efforts. He was the head of the British team that worked on the Manhattan Project during World War II.
"The discovery of the neutron and its properties was central to the extraordinary developments in atomic physics in the first half of the 20th century. Early in the century, Ernest Rutherford used alpha particle scattering to discover that an atom has its mass and electric charge concentrated in a tiny nucleus. By 1920, isotopes of chemical elements had been discovered, the atomic masses had been determined to be approximately integer multiples of the mass of the hydrogen atom, and the atomic number had been identified as the charge on the nucleus. Throughout the 1920s, the nucleus was viewed as composed of combinations of protons and electrons, the two elementary particles known at the time, but that model presented several experimental and theoretical contradictions.
"The essential nature of the atomic nucleus was established with the discovery of the neutron by James Chadwick in 1932 and the determination that it was a new elementary particle, distinct from the proton.
"The uncharged neutron was immediately exploited as a new means to probe nuclear structure, leading to such discoveries as the creation of new radioactive elements by neutron irradiation (1934) and the fission of uranium atoms by neutrons (1938). The discovery of fission led to the creation of both nuclear power and nuclear weapons by the end of World War II. Both the proton and the neutron were presumed to be elementary particles until the 1960s, when they were determined to be composite particles built from quarks. "
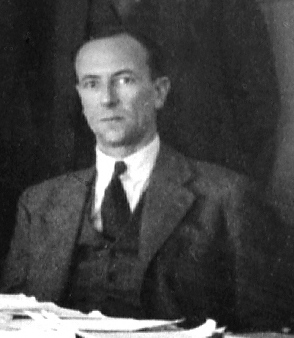
| Year: 1928 | PT id = 1378, Type = structure |
Dirac Equation
Dirac, P. A. M. (1928). "The Quantum Theory of the Electron". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 117 (778): 610–624. PDF of paper.
"The Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-?1/2? massive particles, called Dirac particles, such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity and was the first theory to fully account for special relativity in the context of quantum mechanics. The equation is validated by its rigorous accounting of the observed fine structure of the hydrogen spectrum and has become vital in the building of the Standard Model pf particle physics.

"The equation also implied the existence of a new form of matter, antimatter, previously unsuspected and unobserved. The existence of antimatter was experimentally confirmed several years later. It also provided a theoretical justification for the introduction of several component wave functions in Pauli's phenomenological theory of spin. The wave functions in the Dirac theory are vectors of four complex numbers (known as bispinors), two of which resemble the Pauli wavefunction in the non-relativistic limit, in contrast to the Schrödinger equation, which described wave functions of only one complex value."
If you require deeper dive into quantum spin and the Dirac equation, these two linked videos by Physics Explained will be of interest. The videos discuss the history and the mathematics of the equation. The videos show that the Dirac formulation of the relativistic electron inevitably has four answers or solutions which correspond to the:
- Spin-up electron
- Spin-down electron
- Spin-up positron (anti-electron)
- Spin-down positron
- The result also shows that the spin must be +1/2 or –1/2.
| Year: 1927 | PT id = 1377, Type = structure |
Fifth Solvay Conference on Physics
"The most famous conference was the fifth Solvay Conference on Physics, which was held from 24 to 29 October 1927. The subject was Electrons and Photons and the world's most notable physicists met to discuss the newly formulated quantum theory. The leading figures were Albert Einstein and Niels Bohr. Seventeen of the 29 attendees were or became Nobel Prize winners, including Marie Skłodowska-Curie who, alone among them, had won Nobel Prizes in two separate scientific disciplines. The anti-German prejudice that had prevented Einstein and others from attending the Solvay conferences held after the First World War had melted away. Essentially all of those names who had contributed to the recent development of the quantum theory were at this Solvay Conference, including Bohr, Born, de Broglie, Dirac, Heisenberg, Pauli, Planck, Lorentz, Compton, Ehrenfest, and Schrödinger. Heisenberg commented:
"Through the possibility of exchange between the representatives of different lines of research, this conference has contributed extraordinarily to the clarification of the physical foundations of the quantum theory. It forms, so to speak, the outward completion of the quantum theory."
"The photo taken of this conference's participants is sometimes entitled 'The Most Intelligent Photo Ever Taken', for its depiction of the world's leading physicists gathered together in one shot."

A. Piccard, E. Henriot, P. Ehrenfest, E. Herzen, Th. De Donder, E. Schrödinger, J.E. Verschaffelt, W. Pauli, W. Heisenberg, R.H. Fowler, L. Brillouin;
P. Debye, M. Knudsen, W.L. Bragg, H.A. Kramers, P.A.M. Dirac, A.H. Compton, L. de Broglie, M. Born, N. Bohr;
I. Langmuir, M. Planck, M. Skłodowska-Curie, H.A. Lorentz, A. Einstein, P. Langevin, Ch. E. Guye, C.T.R. Wilson, O.W. Richardson
Fifth conference participants, 1927. Institut International de Physique Solvay in Leopold Park.
| Year: 1926 | PT id = 1376, Type = structure |
Born Rule
Born, M. Zur Quantenmechanik der Stoßvorgänge. Zeitschrift für Physik, 37, 863–867 (1926).
"Max Born was a German–British theoretical physicist who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics, and supervised the work of a number of notable physicists in the 1920s and 1930s. He shared the 1954 Nobel Prize in Physics with Walther Bothe 'for his fundamental research in quantum mechanics, especially for his statistical interpretation of the wavefunction.'
"The Born rule is a postulate of quantum mechanics that gives the probability that a measurement of a quantum system will yield a given result. In one commonly used application, it states that the probability density for finding a particle at a given position is proportional to the square of the amplitude of the system's wavefunction at that position. So is the wave function is ψ, the probability of finding the electron is |ψ|2."
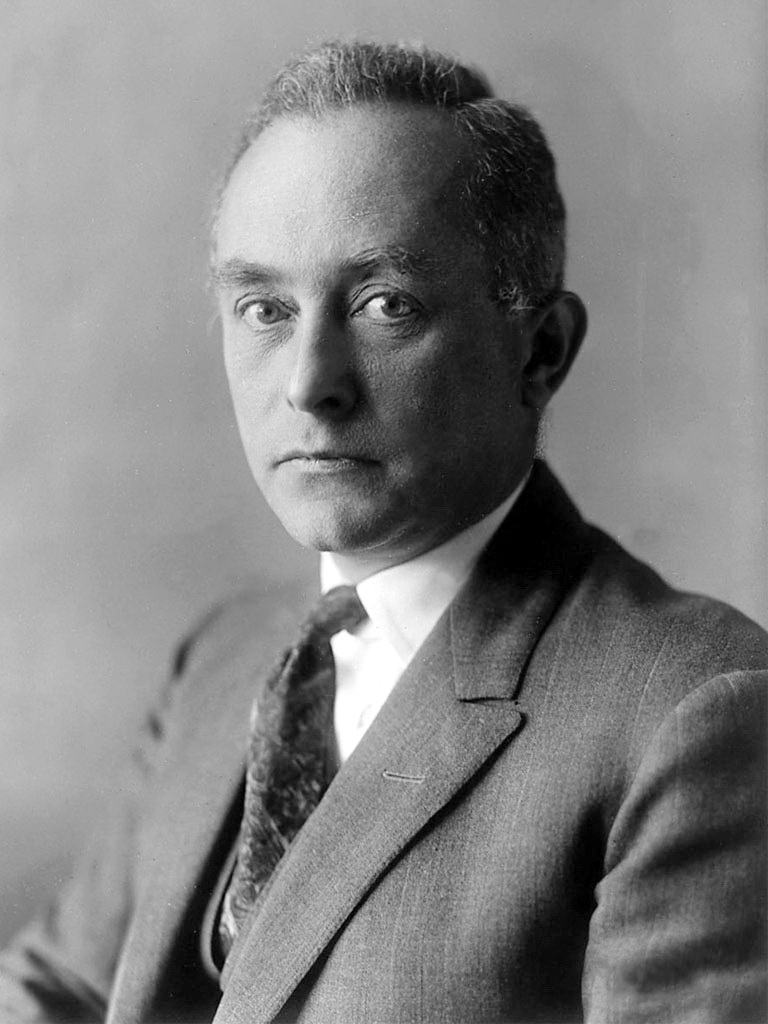
| Year: 1926 | PT id = 1375, Type = structure |
Schrödinger Wave Equation
Schrödinger, E. Quantisierung als Eigenwertproblem (Quantization as an eigenvalue problem) (Parts I–IV). Annalen der Physik, 79, 361–376; 489–527; 734–756; 80, 437–490 (1926).
"Erwin Schrödinger was an Austrian–Irish theoretical physicist who developed fundamental results in quantum theory. In particular, he is recognised for devising the Schrödinger equation, an equation that provides a way to calculate the wave function of a system and how it changes dynamically in time."
"A special case of the Schrödinger equation is the position-space Schrödinger equation for a single nonrelativistic particle in one dimension:
"The ψ is a wave function, a function that assigns a complex number to each point x at each time t. The parameter m is the mass of the particle, and V(x,t) is the potential energy function that represents the environment in which the particle exists. The constant i is the imaginary unit, and ħ is the reduced Planck constant, which has units of action (energy multiplied by time).
"Schrödinger coined the term 'quantum entanglement' in 1935. Schrödinger shared the 1933 Nobel Prize in Physics with Paul Dirac 'for the discovery of new productive forms of atomic theory.''
"The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. Conceptually, the Schrödinger equation is the quantum counterpart of Newton's second law in classical mechanics. Given a set of known initial conditions, Newton's second law makes a mathematical prediction as to what path a given physical system will take over time. The Schrödinger equation gives the evolution over time of the wave function, the quantum-mechanical characterisation of an isolated physical system. The equation was postulated by Schrödinger based on a postulate of Louis de Broglie that all matter has an associated matter wave. The equation predicted bound states of the atom in agreement with experimental observations."

| Year: 1925 | PT id = 1374, Type = structure |
Heisenberg’s Matrix Mechanics and the Uncertainty Principle
Heisenberg, W. Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. (On the quantum-theoretical reinterpretation of kinematic and mechanical relationships.) Zeitschrift für Physik, 33, 879–893 (1925); Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. (On the intuitive content of quantum-theoretical kinematics and mechanics. "The Uncertainty Principle") Zeitschrift für Physik, 43, 172–198 (1927).
"Werner Karl Heisenberg was a German theoretical physicist, one of the main pioneers of the theory of quantum mechanics. Heisenberg published his Umdeutung paper in 1925, a major reinterpretation of old quantum theory. In the subsequent series of papers with Max Born and Pascual Jordan, during the same year, his matrix formulation of quantum mechanics was substantially elaborated. He is also known for the uncertainty principle, which he published in 1927. He received the Nobel Prize in Physics in 1932 'for the creation of quantum mechanics'."

| Year: 1925 | PT id = 1373, Type = structure |
Pauli and The Exclusion Principle
Pauli, W. Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren. Zeitschrift für Physik, 31, 765–783 (1925).
"Wolfgang Pauli was an Austrian–Swiss theoretical physicist and a pioneer of quantum mechanics. In 1945, after having been nominated by Albert Einstein, Pauli received the Nobel Prize in Physics 'for the discovery of the Exclusion Principle, also called the Pauli Principle'. The discovery involved spin theory.
"The Pauli exclusion principle (German: Pauli-Ausschlussprinzip) states that two or more identical particles with half-integer spins (i.e. fermions) cannot simultaneously occupy the same quantum state within a system that obeys the laws of quantum mechanics. This principle was formulated by Austrian physicist Wolfgang Pauli in 1925 for electrons, and later extended to all fermions with his spin–statistics theorem of 1940.
"In the case of electrons in atoms, the exclusion principle can be stated as follows: in a poly-electron atom it is impossible for any two electrons to have the same two values of all four of their quantum numbers, which are: n, the principal quantum number; ℓ, the azimuthal quantum number; mℓ, the magnetic quantum number; and ms, the spin quantum number.
"If two electrons reside in the same orbital, then their values of n, ℓ, and mℓ are equal. In that case, the two values of ms (spin) pair must be different. Since the only two possible values for the spin projection ms are +1/2 and –1/2, it follows that one electron must have ms = +1/2 and one ms = –1/2.
"To preserve the conservation of energy in beta decay, Pauli proposed the existence of a small neutral particle, dubbed the neutrino by Enrico Fermi, in 1930. Neutrinos were first detected in 1956. "
| Year: 1924 | PT id = 1372, Type = structure |
de Broglie and Wave–Particle Duality
de Broglie, L. Recherches sur la théorie des quanta. Annales de Physique, 3, 22–128 (1925). (Doctoral thesis, submitted 1924)
"Louis Victor Pierre Raymond, 7th Duc de Broglie was a French theoretical physicist and aristocrat known for his contributions to quantum theory. In his 1924 Ph.D. thesis, de Broglie postulated the wave nature of electrons and suggested that all matter has wave properties.
"This concept, now known as the de Broglie hypothesis, an example of wave–particle duality, and forms a central part of the theory of quantum mechanics. In 1929, de Broglie won the Nobel Prize in Physics, after the wave-like behaviour of matter was experimentally confirmed in 1927."

| Year: 1916 | PT id = 1371, Type = structure |
Sommerfeld and the Azimuthal and Magnetic Quantum Numbers
Sommerfeld, A. Zur Quantentheorie der Spektrallinien. Annalen der Physik, 51, 1–94 (1916).
"Arnold Sommerfeld was a German theoretical physicist who pioneered developments in both atomic and quantum physics. He also educated and mentored many students for the new era of theoretical quantum physics.
"Sommerfeld introduced the second (azimuthal) and the third (magnetic) quantum numbers ℓ and mℓ. (He also introduced the fine-structure constant and pioneered X-ray wave theory.)
"In quantum mechanics, the azimuthal quantum number ℓ is a quantum number for an atomic orbital that determines its orbital angular momentum and describes aspects of the angular shape of the orbital. The azimuthal quantum number is the second of a set of quantum numbers that describe the unique quantum state of an electron (the others being the principal quantum number n, the magnetic quantum number, mℓ, and the spin quantum number ms).
"Seven of Sommerfeld's doctoral students and postdoctoral supervisees: Werner Heisenberg, Wolfgang Pauli, Peter Debye, Hans Bethe, Linus Pauling, Isidor I. Rabi and Max von Laue went on to win Nobel Prizes in theoretical physics or chemistry. He also supervised at least 30 other famous physicists and chemists."

| Year: 1913 | PT id = 1370, Type = structure |
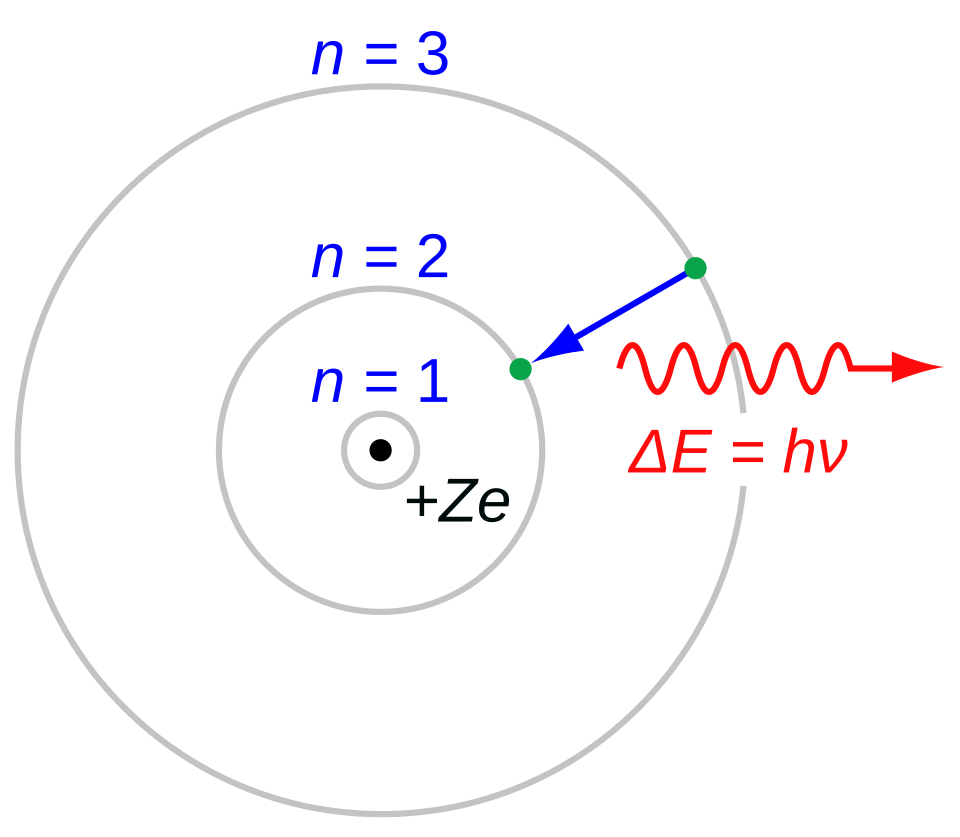
The Bohr Atom
Bohr, N. On the Constitution of Atoms and Molecules (Parts I–III). Philosophical Magazine, 26, 1–25; 476–502; 857–875 (1913).
"In the Bohr model (or the Rutherford–Bohr model) of the hydrogen atom (Z = 1), the negatively charged electron confined to an atomic shell encircles a small, positively charged atomic nucleus. When an electron jumps between orbits, is accompanied by an emitted or absorbed amount of electromagnetic energy (where E = hν). The orbits in which the electron may travel are shown as grey circles; their radius increases as n2, where n is the principal quantum number. The 3 ? 2 transition produces the first line of the Balmer series, and for hydrogen (Z = 1) it results in a photon of wavelength 656 nm (red light).
"The Bohr atom consists of a small, dense atomic nucleus surrounded by orbiting electrons. It is analogous to the structure of the Solar System, but with attraction provided by electrostatic force rather than gravity, and with the electron energies quantised (assuming only discrete values). The Bohr model incorporated some early quantum concepts. Developed from 1911 to 1918 by Niels Bohr and building on Ernest Rutherford's discovery of the atom's nucleus, the model supplanted the plum pudding model of J. J. Thomson only to be replaced by the quantum atomic model in the 1920s.
"The Bohr model's key success lies in explaining the Rydberg formula for hydrogen's spectral emission lines. While the Rydberg formula had been known experimentally, it did not gain a theoretical basis until the Bohr model was introduced. Not only did the Bohr model explain the reasons for the structure of the Rydberg formula, it also provided a justification for the fundamental physical constants that make up the formula's empirical results."
 |
 |
 |
| What is the Periodic Table Showing? | Periodicity |
© Mark R. Leach Ph.D. 1999 –
Queries, Suggestions, Bugs, Errors, Typos...
If you have any:
Queries
Comments
Suggestions
Suggestions for links
Bug, typo or grammatical error reports about this page,please contact Mark R. Leach, the author, using mark@meta-synthesis.com
This free, open access web book is an ongoing project and your input is appreciated.