Periodic Table |
 |
 |
 |
 |
 |
 |
 |
| What is the Periodic Table Showing? | Periodicity |
The INTERNET Database of Periodic Tables
There are thousands of periodic tables in web space, but this is the only comprehensive database of periodic tables & periodic system formulations. If you know of an interesting periodic table that is missing, please contact the database curator: Mark R. Leach Ph.D. The database holds information on periodic tables, the discovery of the elements, the elucidation of atomic weights and the discovery of atomic structure (and much, much more).
Periodic Tables referencing the text string "Samanez", listed by date:
| Year: 1936 | PT id = 777, Type = formulation data misc |
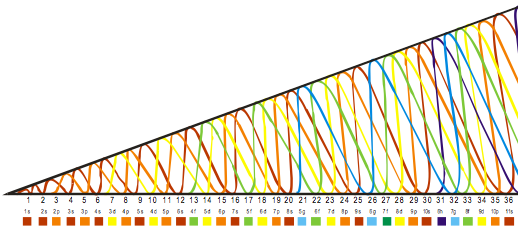
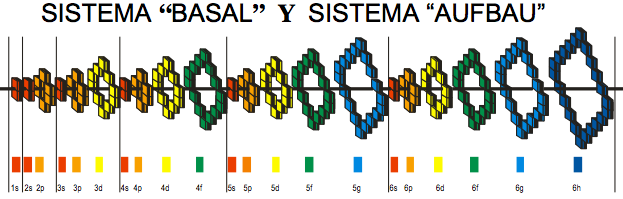
Orbital Filling With Electrons
Students of chemistry are often confused why the orbitals fill with electrons: 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d10, 4p6... etc., because the 3d10 seems to be 'out of sequence'.
This 'out of sequence' difficulity is nicely explained if the orbitals are arranged in a slightly different way:
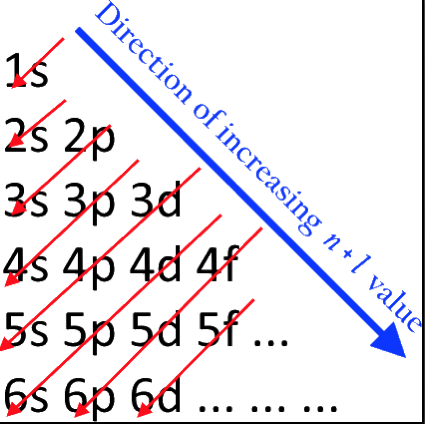
The aufbau principle states that in the ground state of an atom or ion, electrons fill atomic orbitals of the lowest available energy levels before occupying higher levels. For example, the 1s shell is filled before the 2s subshell is occupied. In this way, the electrons of an atom or ion form the most stable electron configuration possible.
The order in which these orbitals are filled is given by the n + ![]() rule, also known as the Madelung rule (after Erwin Madelung), the Janet rule or the diagonal rule.
rule, also known as the Madelung rule (after Erwin Madelung), the Janet rule or the diagonal rule.
Orbitals with a lower n + ![]() value are filled before those with higher n +
value are filled before those with higher n + ![]() values. In this context, n represents the principal quantum number and ? the azimuthal quantum number. The values
values. In this context, n represents the principal quantum number and ? the azimuthal quantum number. The values ![]() = 0, 1, 2, 3 correspond to the s, p, d and f orbital lables.
= 0, 1, 2, 3 correspond to the s, p, d and f orbital lables.
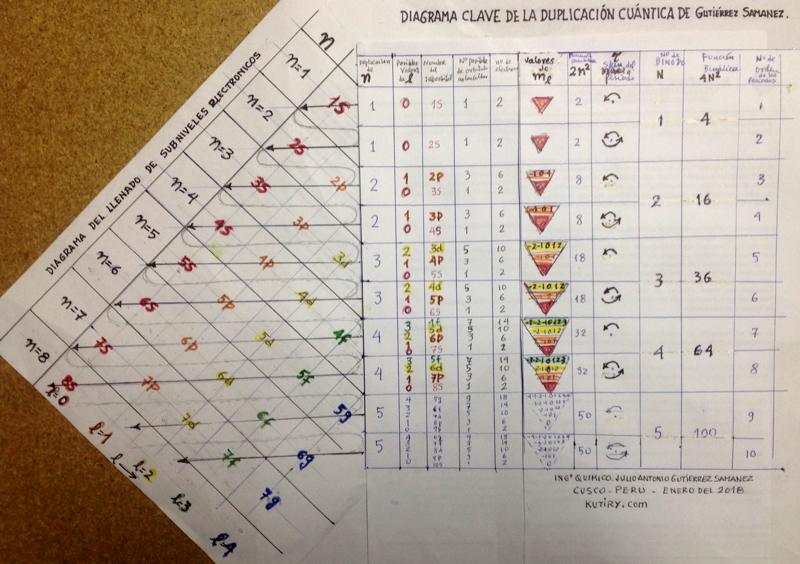
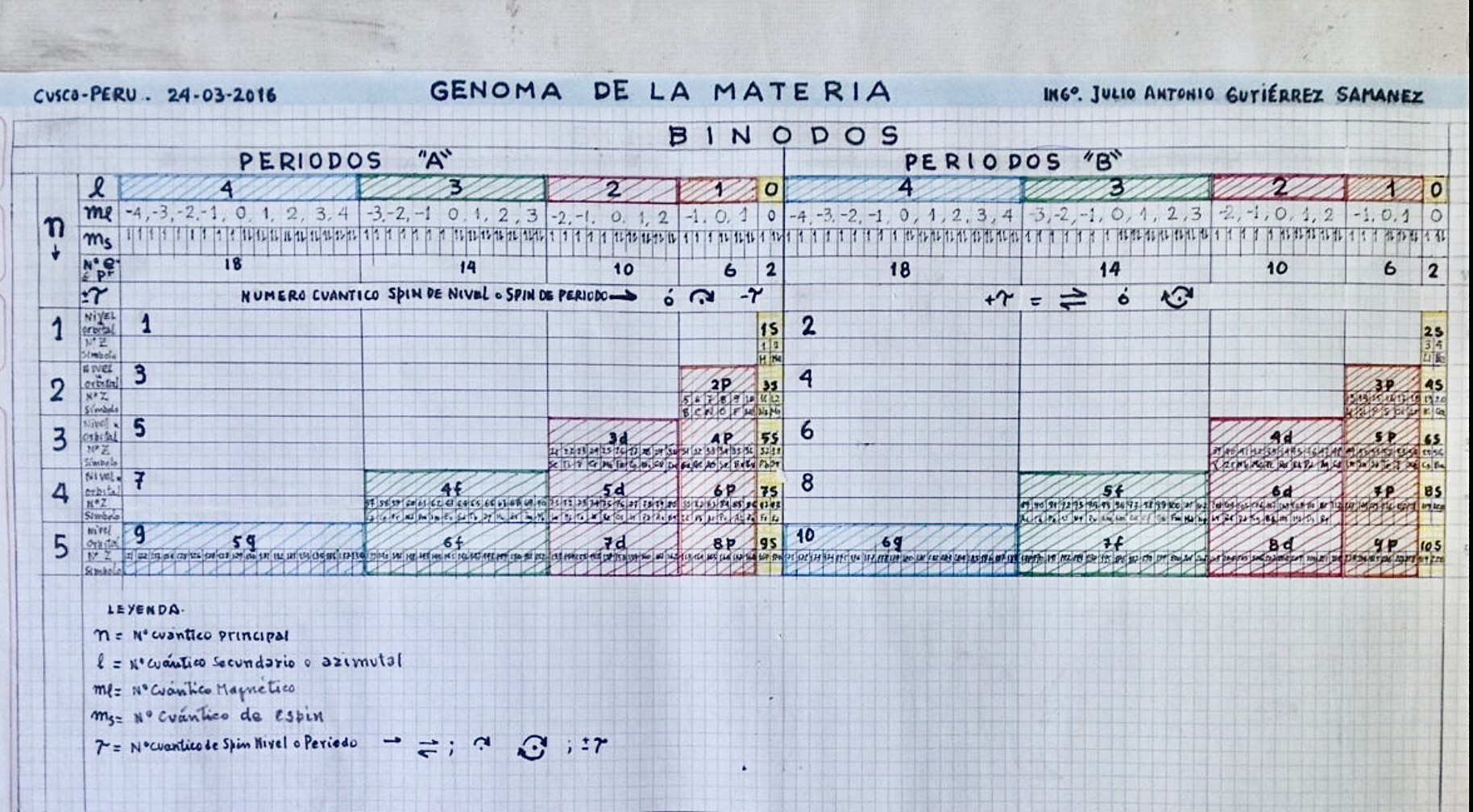
Julio Gutiérrez Samanez writes:
"I send you the diagram below that reconciles quantum mechanics (diagram for filling the electronic cells) with the Janet table or LSPT. Explaining the duplication of periods with the duplication of the quantum number n, and the introduction of Tao (T) spin of the level or spin of the period, which explains the parity of the symmetric periods."
| Year: 1936 | PT id = 909, Type = formulation spiral |
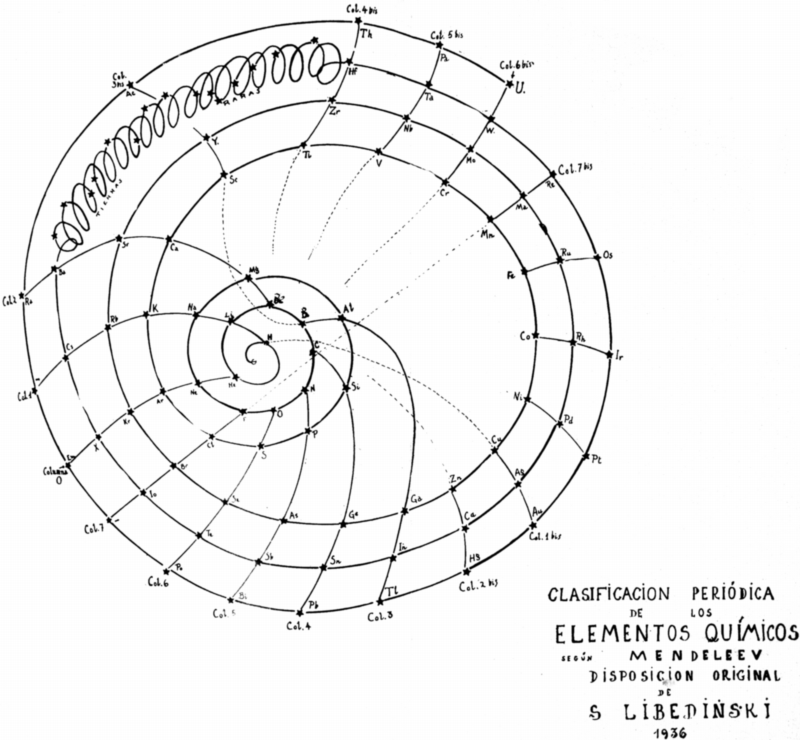
Libedinski's Periodic Classification of The Elements
Simón Libedinski: PERIODIC CLASSIFICATION OF THE ELEMENTS, from his book: Dialectical Materialism, in Nature, in Society and in Medicine, Ediciones Ercilla, Santiago de Chile, 1938, pp 56-57:
"Mendeleev's Table, like that of Werner and others, are not, however, more than flat projections of the actual ordering of the elements. There is as much difference between Mendeleev's Table and the real group as there is between the planisphere and a rotating globe. A rational representation, starting from the simplest element – the negative electron –, would be a spiral line that, surrounding said central point, first gave a small turn, touching only two bodies: hydrogen and helium. From here it would jump to a much larger orbit, in which it would touch eight bodies and then another equal, also of eight. From here, another jump to a much larger orbit, comprising eighteen bodies, and then another equal; from this point one jumps to another orbit, again augmented, comprising thirty-two bodies (including rare earths); and when this round is over, the last one begins, to vanish a short distance.
"In the dialectical grouping of the elements, which I have the satisfaction of exposing, the classic arrangement of the same is respected. Only the arrangement changes, which instead of being rectilinear, is spiral. So I managed to suppress the anomaly of the double columns, and comfortably incorporate the important group of rare earths. I can not give my graphic the name of Tabla, because it is just the opposite: it aims to give the idea of ??space, and of movement in space. The double columns of the Classic Table can be found here as well, but only if you look through the whole, considered as a planetary system of conical shape, with the electron at the vertex. Effectively: column 1 coincides, through space, with column 1a; column 4 with column 4 bis, etc. The dialectical grouping also allows us to easily appreciate the remarkable dialectical character of the properties of matter: these properties are repeated periodically. These are the "returns" to qualities or previous properties, but not exactly equal to those, but only similar: and this resemblance, only to a certain extent. The difference is that that quality, those properties or some characteristic, are exalted to each dialectical return."
Contributed by Julio Antonio Gutiérrez Samanez, Cusco, Peru, March 2018 (using Google Translation)
| Year: 1959 | PT id = 1160, Type = formulation review |
Mendoza's Neuvo Sistema Periodico
A memorial work, Ley De Configuraciones Electronicas, published posthumously in 1965 to honor Oswaldo Baca Mendoza (1908–1962 Cusco, Peru) and his 1959 Neuvo Sistema Periodico. Download the full PDF file (in Spanish).


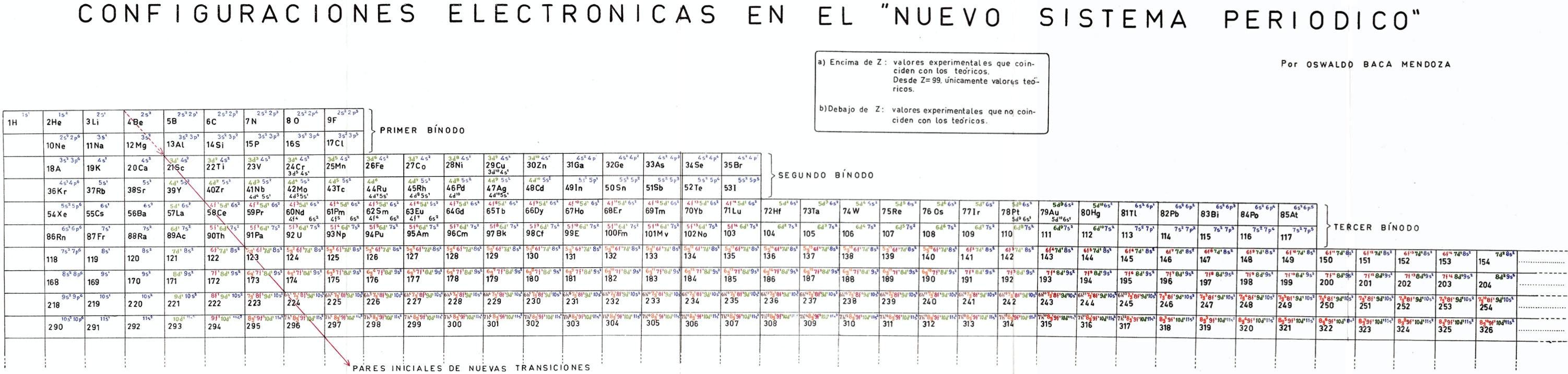
Thanks to Julio Gutierrez Samanez for the infomaton, etc.
| Year: 2004 | PT id = 1100, Type = formulation review |
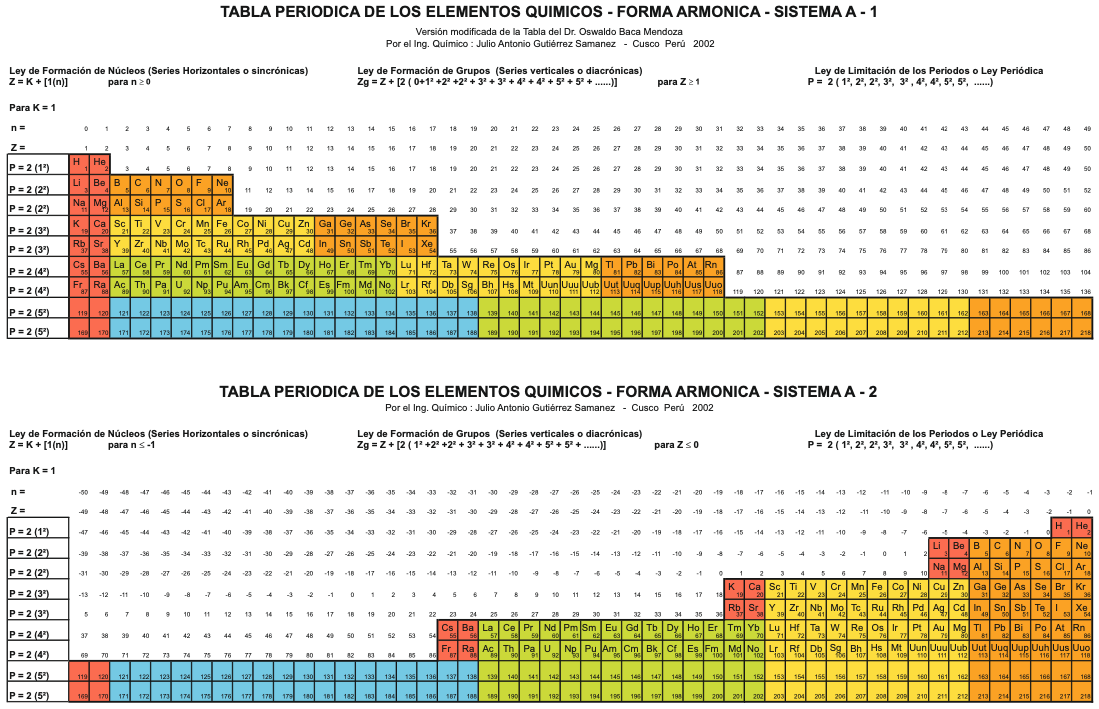
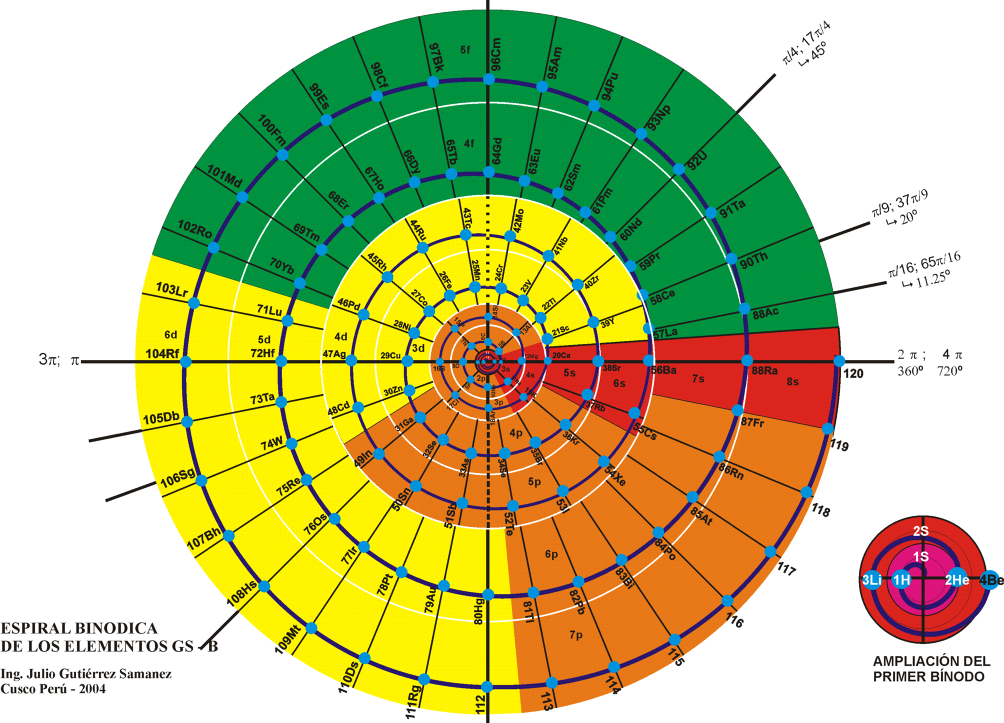
Sistema Periódico Armonico de Gutierrez-Samanez
A digitised 2004 book by book by Julio Gutiérrez-Samanez.
Julio writes:
"These matrix tables are inspired by the method used by the Peruvian chemist Oswaldo Baca Mendoza (1908-1962).
"The tables are read in this way: The Law of Formation of nuclei generates all the horizontal series Z, is dependent on n (series of integers numbers) and a constant K = 1. In the step-to-right tables (n) it will be equal to or greater than 0. In Janet's Left-Step table, (n) will be less than or equal to (-1). The values of this series Z will serve as a constant for the second law.
"The Group Formation Law or vertical series. Its generate the numeric values of the columns either from left to right or from right to left. In system A -1: With the first law: n = 0, then Z = 1. The vertical series Zg = 1, 3 11, 19, 37, 55, 87 ... That is: 1H, 3Li, 11Na, 19K, 37Rb, 55Cs, 87Fr, 119, 169 ... Changing the values of n or Z, all the columns of the table will be obtained.
"In system A -2: With the first law: on the left, n = -1, then Z = 0. The vertical series Zg will be: 2He, 10Ne, 18Ar, 36Kr, 54Xe, 86Rn, 118Og, 168, 218. .. Similarly, changing the n or Z values, we can fills the columns of the table. In system B -1: With the first law: for n = 0, then Z = 1. The vertical series Zg will be; 1H, 3Li, 5B, 13Al, 21Sc, 39Y, 57La, 89Ac, 121, 171 ... By varying the values of n or Z, the entire table is filled. In system B -2: (Its mathematizes the Janet system). With the first law: on the left, for n = -1, then Z = 0.
"The vertical series Zg will be; 2He, 4Be, 12Mg, 20Ca, 38Sr, 56Ba, 88Ra, 120, 170, 220 ... By varying the values of n or Z, the entire table is filled. The third law of the limiting the periods or periodic law, appears graphically, by comparison between rows: For example: in table B -1, in column Z = 3, after 1H and 2He, en of the first horizontal line, the value 3 appears, which is already entered in the first column as 3Li, therefore, that part of the first horizontal row (from 3 to 50) is deleted.
"The same happens with the number 5 in column 3, which is already in the first column as 5B, therefore it will be deleted in the second row from 5 to 52. The same applies to pair 13, 21 of the column Z = 9, same, with the pair 39, 57 of the column Z = 19 and of the pair 89, 121 of the column Z = 33. For that reason the periods: P are duplicated function: 2 (1 ^ 2), 2 (1 ^ 2), 2 (2 ^ 2), 2 (2 ^ 2), 2 (3 ^ 2), 2 (3 ^ 2) .... = 2, 2, 8, 8, 18, 18, 32, 32 ... and the forms are exact and staggered. The colors represent the quantum functions: s (red), p (orange), d (yellow), f (green), g (blue)."
| Year: 2008 | PT id = 313, Type = formulation |
Nuevo Modelo Mathemático Tabla Periódica
Julio Antonio Gutiérrez Samanez presents his Periodic Table formulation ideas in a 2006 PDF paper (in Spanish):
| Year: 2008 | PT id = 468, Type = formulation spiral 3D |
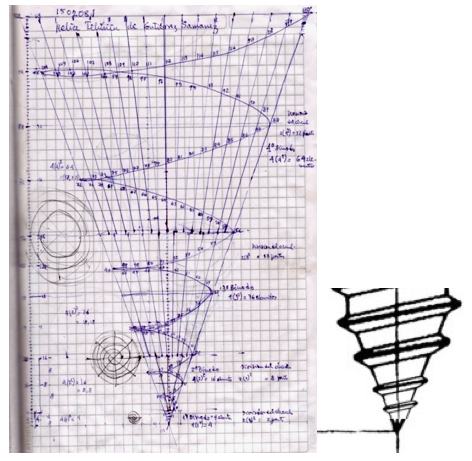
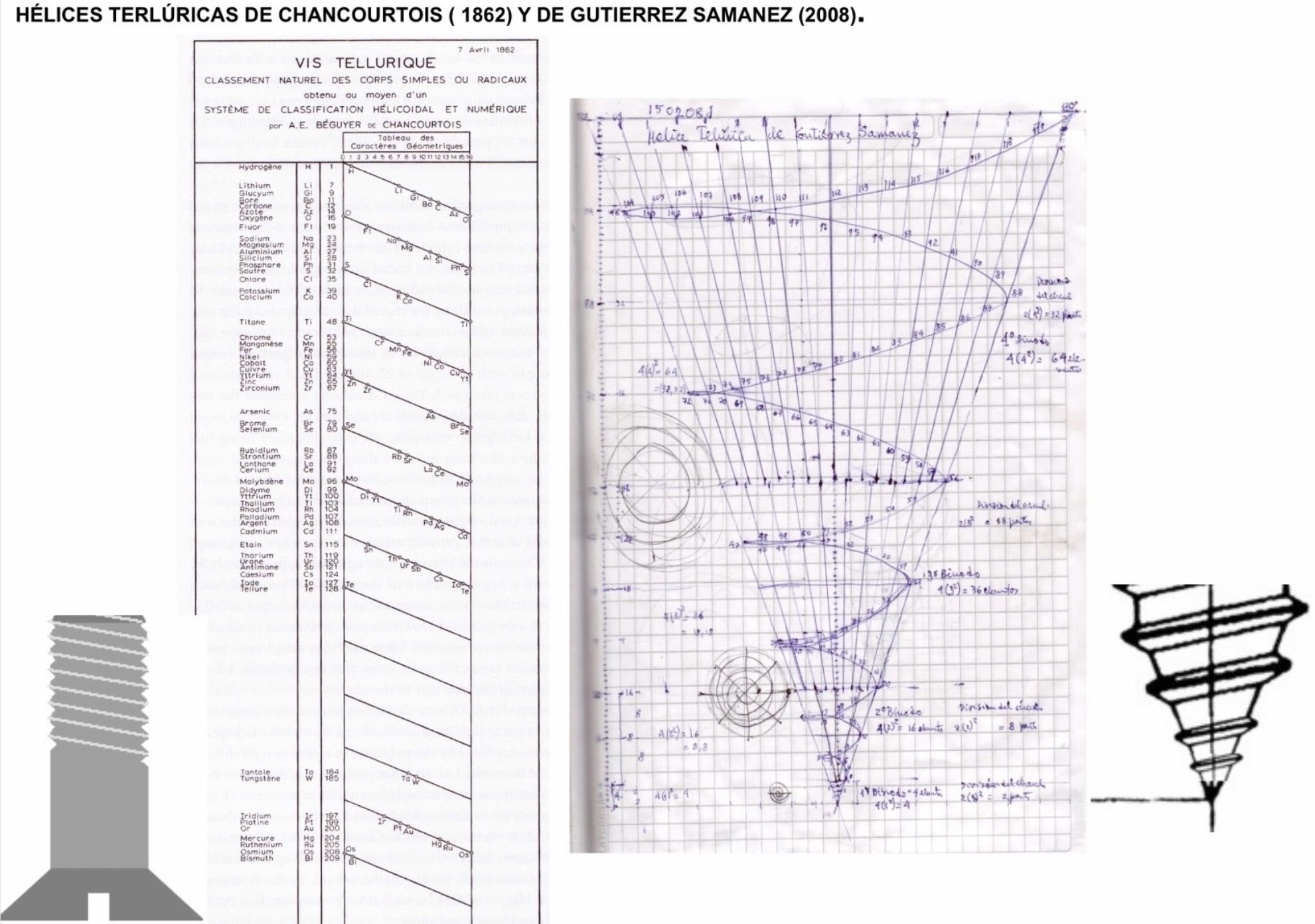
Teluric Helix from Gutierrez Samanez
The Teluric Helix from Gutierrez Samanez is inspired by the telluric helix Chancortois (1864) with the difference that the sequence of the elements are rolled into a cone shape rather than a cylinder:
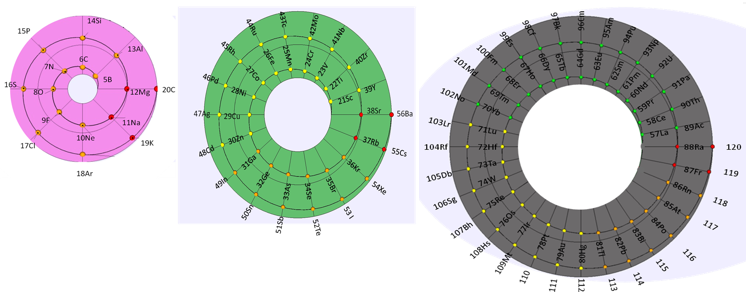

| Year: 2010 | PT id = 388, Type = formulation misc |
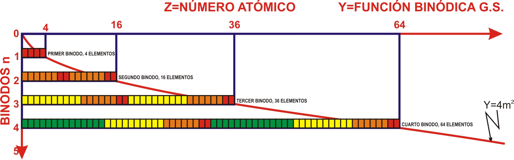
Khipu or Quipu Periodic Table
The Khipu or Quipu or Talking Knot Periodic Table, developed by Julio Antonio Gutierrez Samanez.
Google translated from the Spanish pdf file:
"As a result of bringing together each pair of periods in a single function or binod, the author has found a new regular on the subject, which has been defined as a new quantum number, since the number of orders or regulations binod growth elements in the table, under the appearance of pairs of new types of quantum structures or periods whose organization responds to a simple mathematical function: a parable of the type Y = 4 X ^ 2 - In this case report: a) That the strings correspond to pairs of periods or binod and knots are double for items with orbital s (in red), six nodes for p in orange, 10 yellow d knots and 14 knots for green f . b) That in each binod or rope, appear regularly in pairing mode or dual, new quantum or orbital structures, such as moving from within the orbital previous binod.":
| Year: 2013 | PT id = 592, Type = formulation 3D spiral |
3D Left Step Periodic Table
By Masahiko Suenaga, Kyushu University, Japan a 3D Left Step Periodic Table.
"Inspired by the work of Dr. Tsimmerman and Dr. Samanez, I have created a new 3D Left Step Periodic Table, which resembles to Mt. Fuji, recently registered as a World Heritage site. For more information, please visit my website":
| Year: 2014 | PT id = 643, Type = formulation 3D |
Gutierrez Samanez's Binodic Form of the Periodic Table (Video)
| Year: 2016 | PT id = 1221, Type = formulation |
Genoma de la Materia
By Julio Antonio Gutiérrez Samanez, Genome of Matter:
| Year: 2018 | PT id = 936, Type = formulation 3D |
Sistema Periódico Binodico
By Julio Antonio Gutiérrez Samanez, who writes:
"Sistema Periódico Binodico. Nuevo Paradigma Matematizado. I have followed the work of the wise Mendeleev, of Emil de Chancourtois, of Charles Janet; inspired by the work of my countryman Dr. Oswaldo Baca Mendoza. It is in Spanish but soon I will have the English version."
| Year: 2018 | PT id = 946, Type = formulation 3D |
Periodical System (Binodic Form): a new mathematical paradigm
By Julio Antonio Gutiérrez Samanez, who writes:
"System devised and prepared by the Peruvian chemical engineer, Julio Antonio Gutiérrez Samanez, deals with a new conception of Mendeleev's Law as a mathematical function and a new description of the process of forming the series of chemical elements according to mathematical laws and dialectical processes of changes quantitative and qualitative under a dynamic spiral architecture in 3D, which is postulated as a new scientific paradigm."
| Year: 2019 | PT id = 1064, Type = formulation |
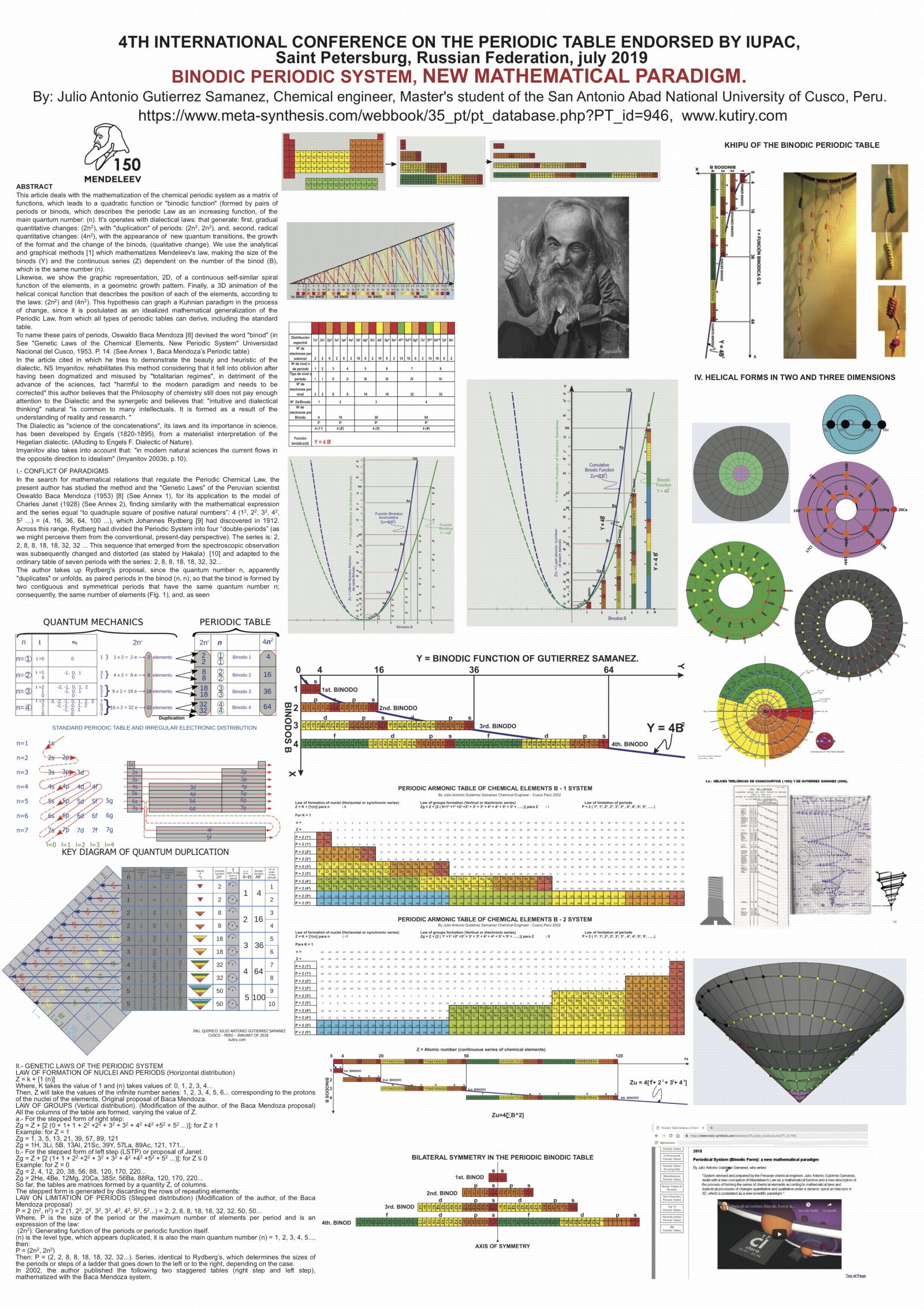
Samanez's Binodic Periodic System, New Mathematical Paradigm Poster
Julio Antonio Gutierrez Samanez (Master's student in chemical engineering at the San Antonio Abad National University of Cusco, Peru) presented a poster at the 4th International Conference on the Periodic Table arranged by IUPAC, Saint Petersburg, Russian Federation, July 2019. See the high resolution .PDF file.
More here and at kutiry.com
| Year: 2021 | PT id = 1186, Type = formulation |
Helix vs. Screw
Julio Antonio Gutierrez Samanez writes:
Until today, when they write about the work of Chancourtois and his telluric helix wound in a cylinder, still no one alludes to this other telluric helix wound in a cone or screw, the idea is the same: a rope that winds a geometric solid.
The first was devised in 1862, the other in 2008 (146 years later). But, there is a big epistemological difference. In the first, the elementary series presented was: 8, 8, 8, 8, 8 ..., etc., in the second it is: 2, 2, 8, 8, 18, 18, 32, 32. Furthermore, the division of conical radii is regulated by the function 2 (n ^ 2) = 2, 8, 18, 32...
Each binode has two spirals or two periods with the same number of elements, which correspond to the function 4 (n ^ 2). I don't think it is a discovery, it is just the conclusion of the contributions of Rydberg, Janet, and, of course, Chancourtois.
| Year: 2021 | PT id = 1222, Type = formulation 3D |
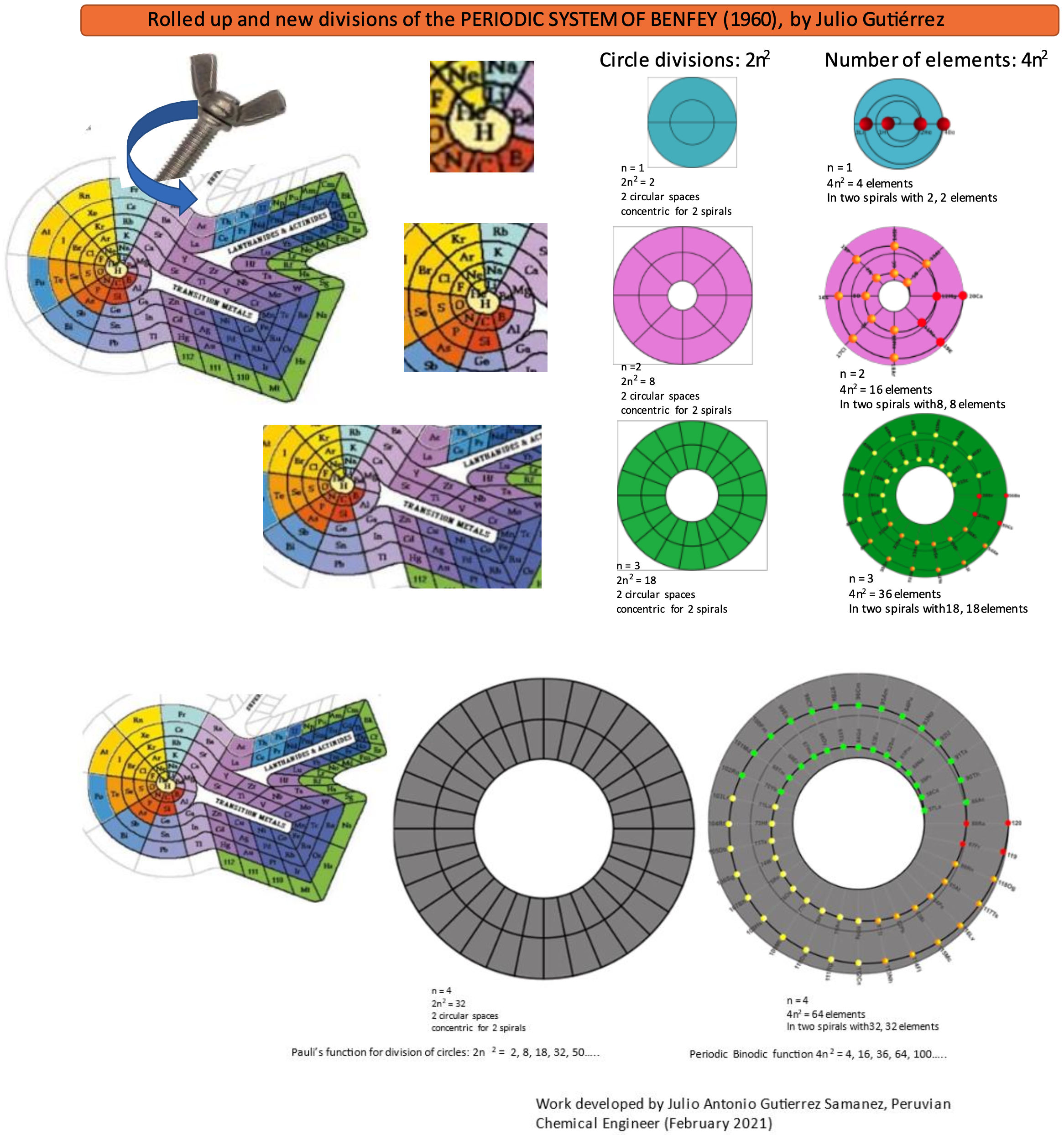
Rolled-up Version of Benfey's Periodic System
Rolled-up Version of Benfey's Periodic System by Julio Antonio Gutiérrez Samanez. More on the YouTube video here.
| Year: 2022 | PT id = 1241, Type = data |
Electronegativity Seamlessly Mapped Onto Various Formulations of The Periodic Table
A discussion on the Google Groups Periodic Table Discussion List, involving a René Vernon, Nawa Nagayasu & Julio Samanez (all contributors this database) lead to the development of the representations below, showing electronegativity seamlessly mapped onto a modified Left-Step Periodic Table:
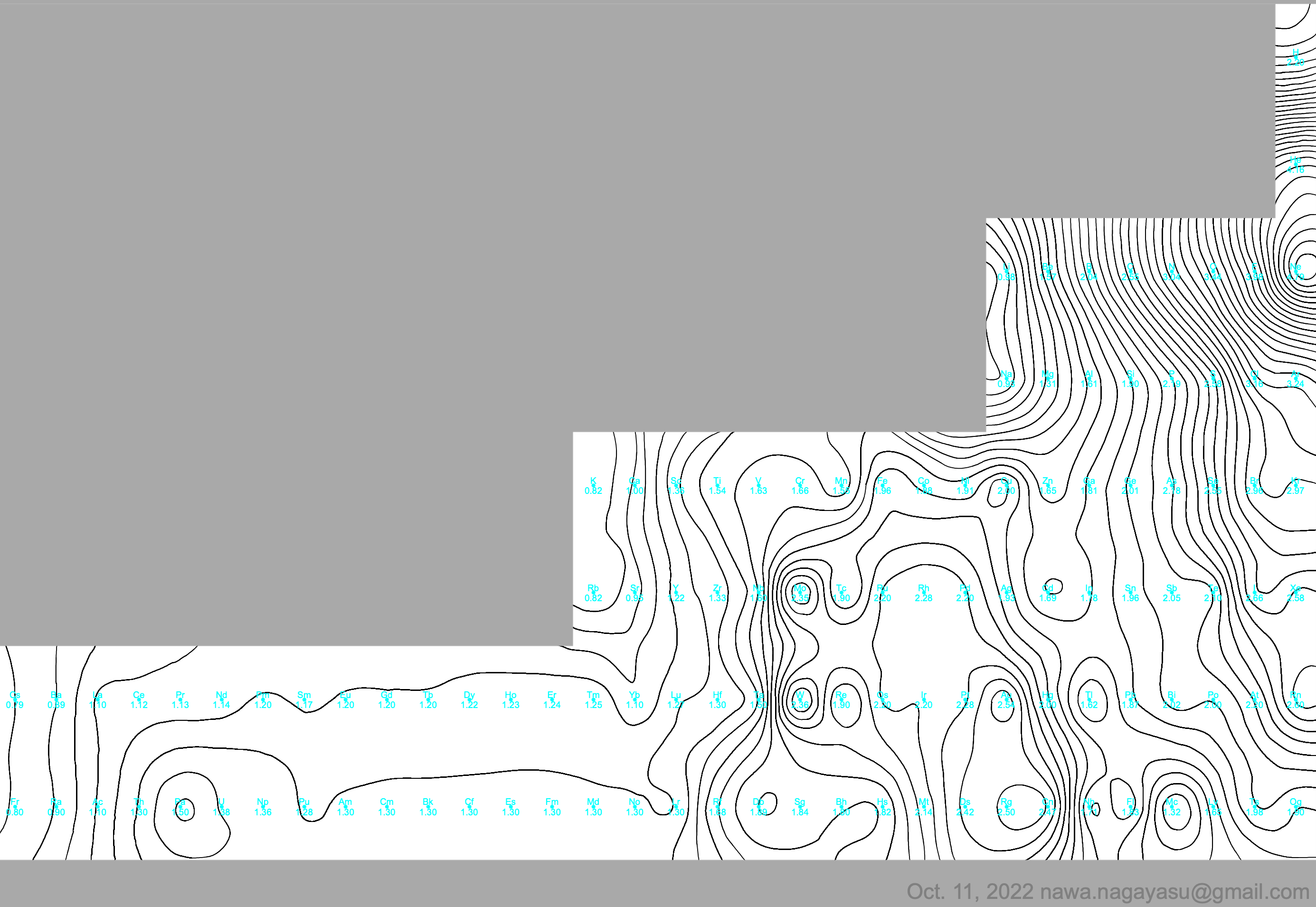
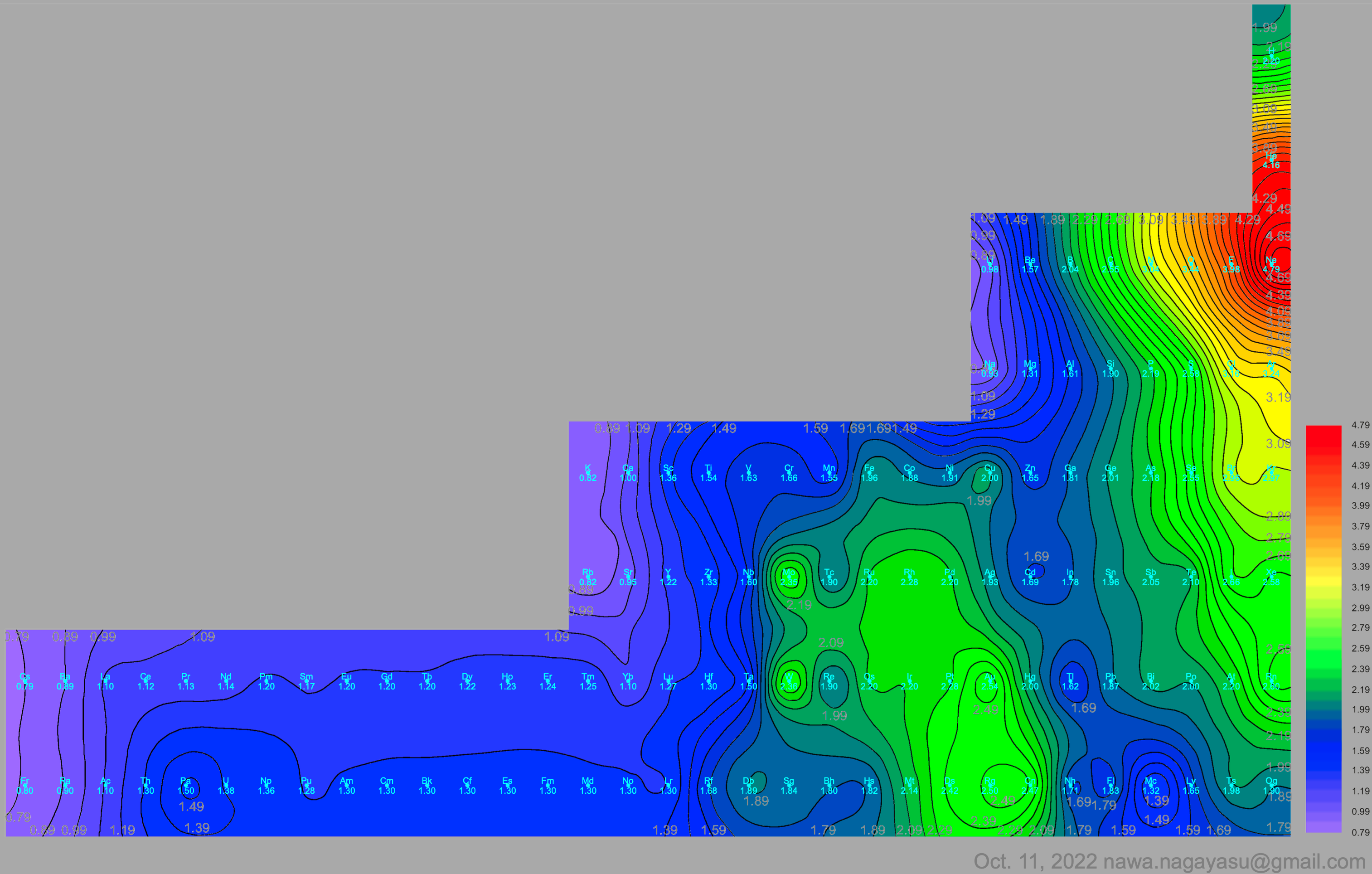
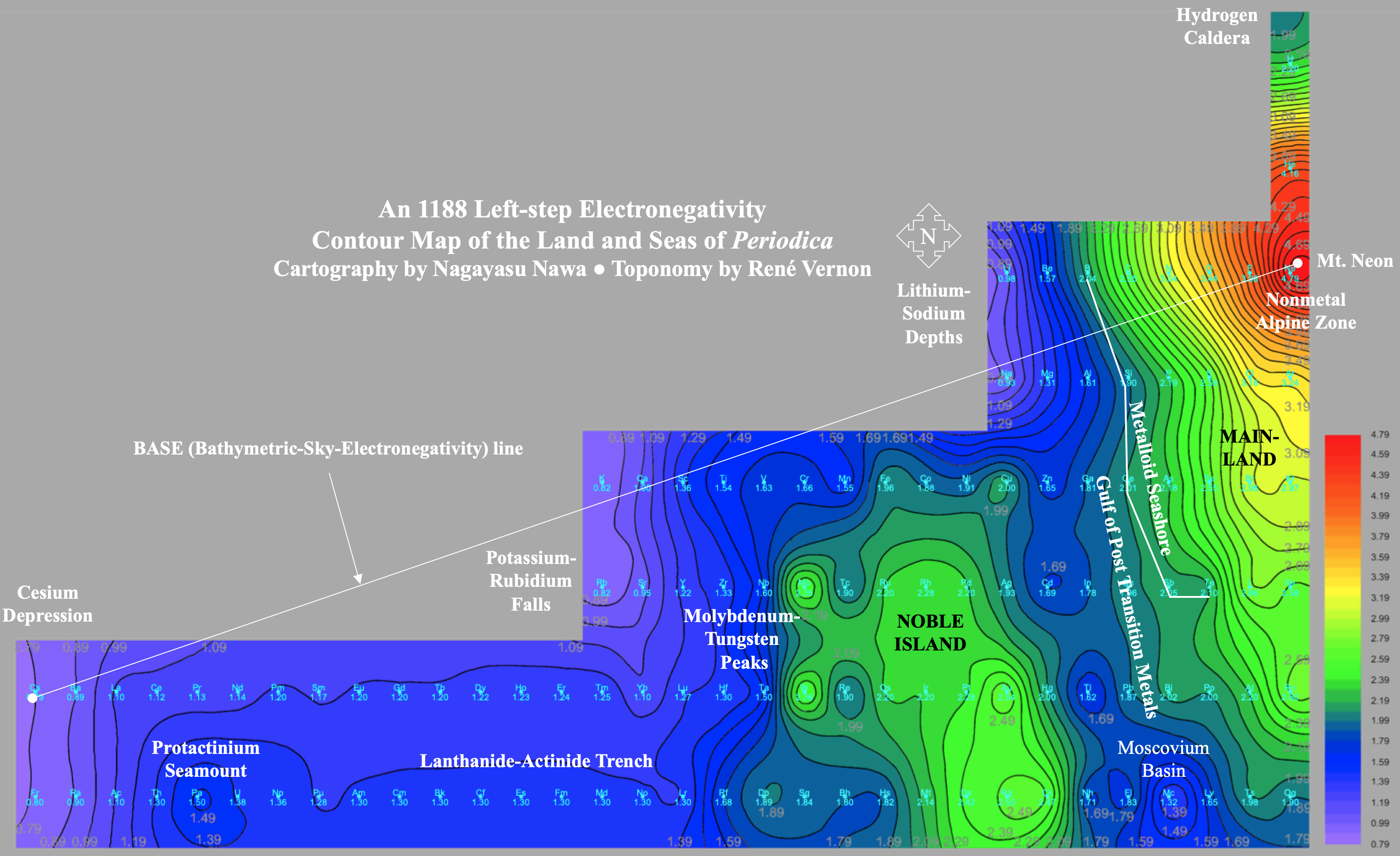
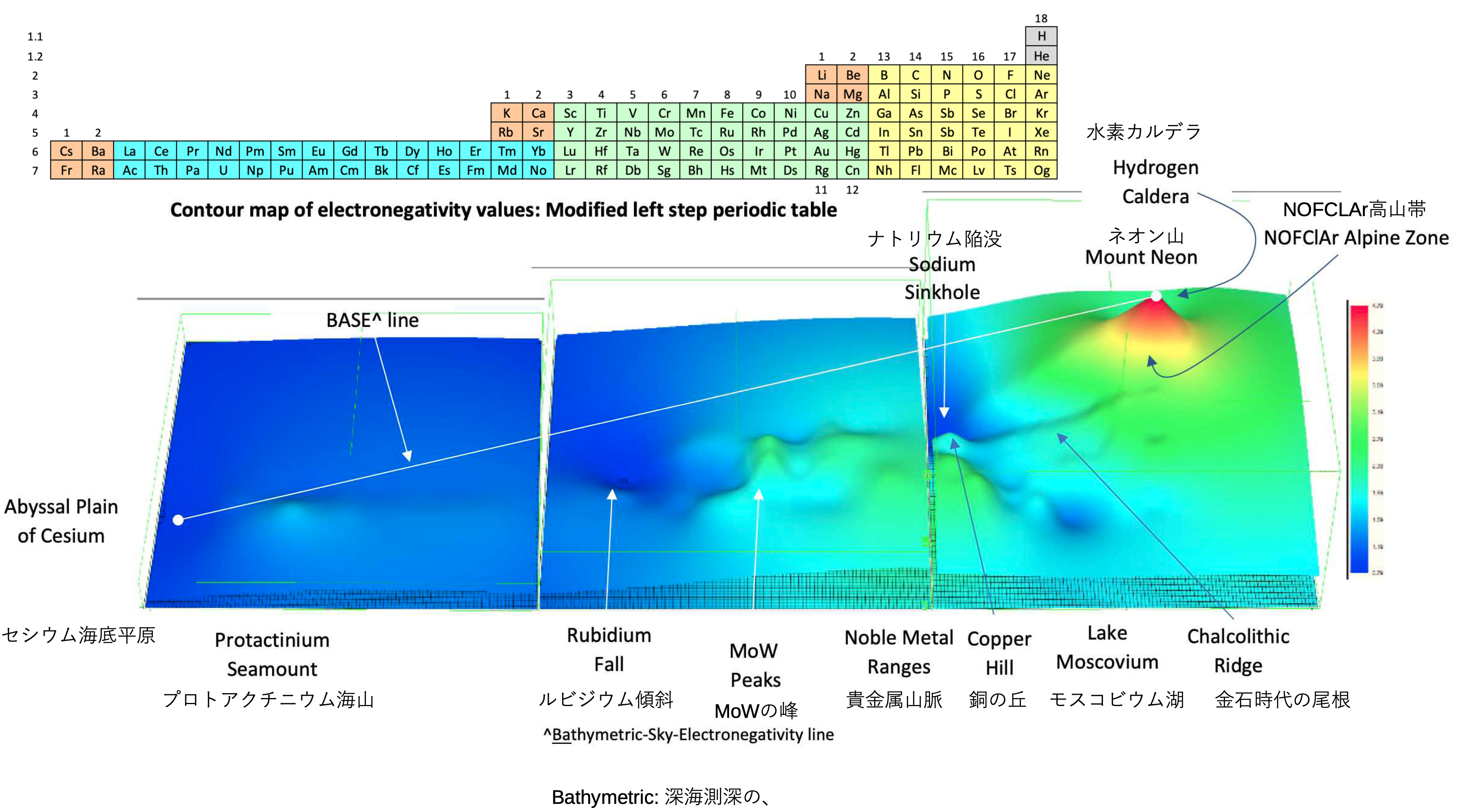
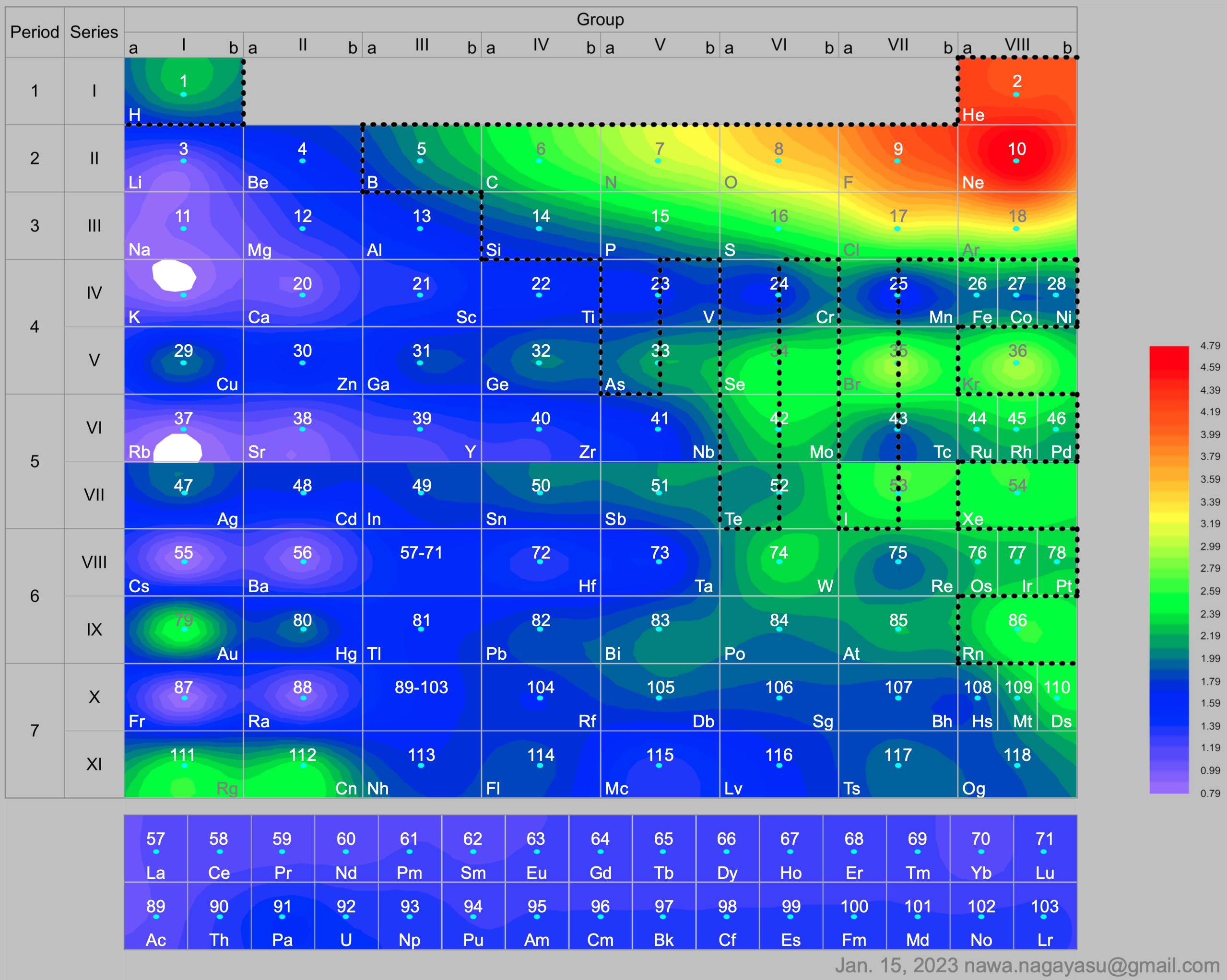
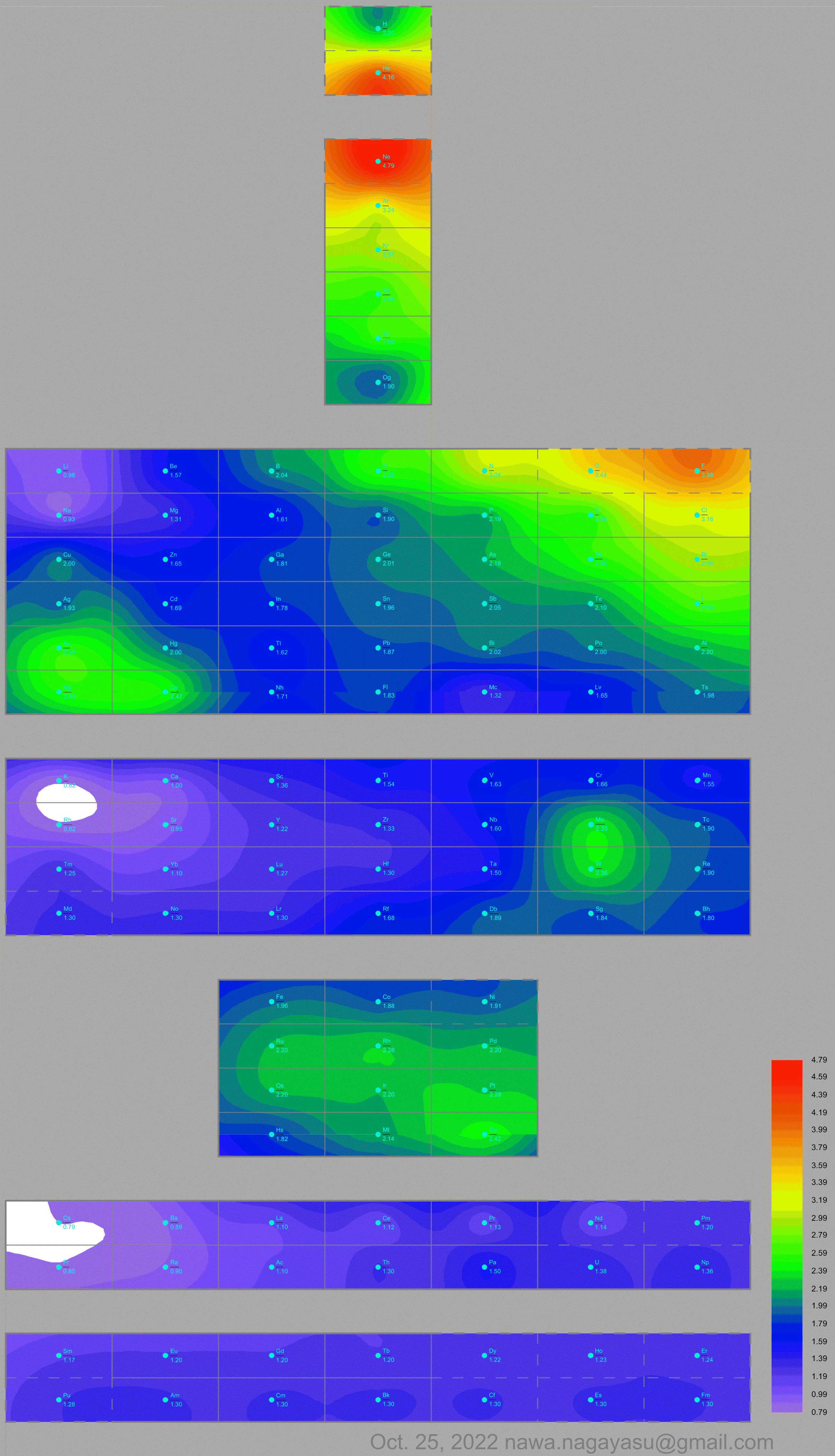
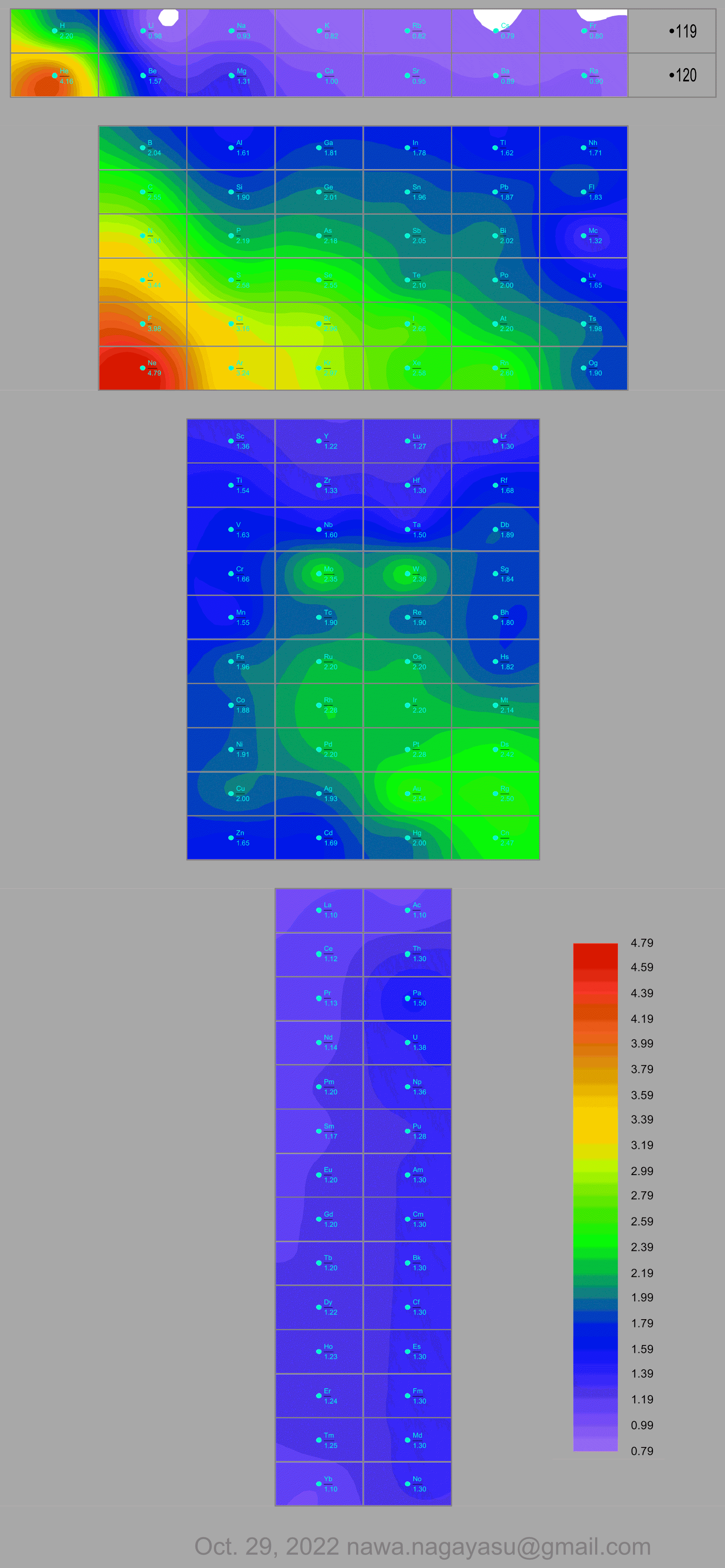
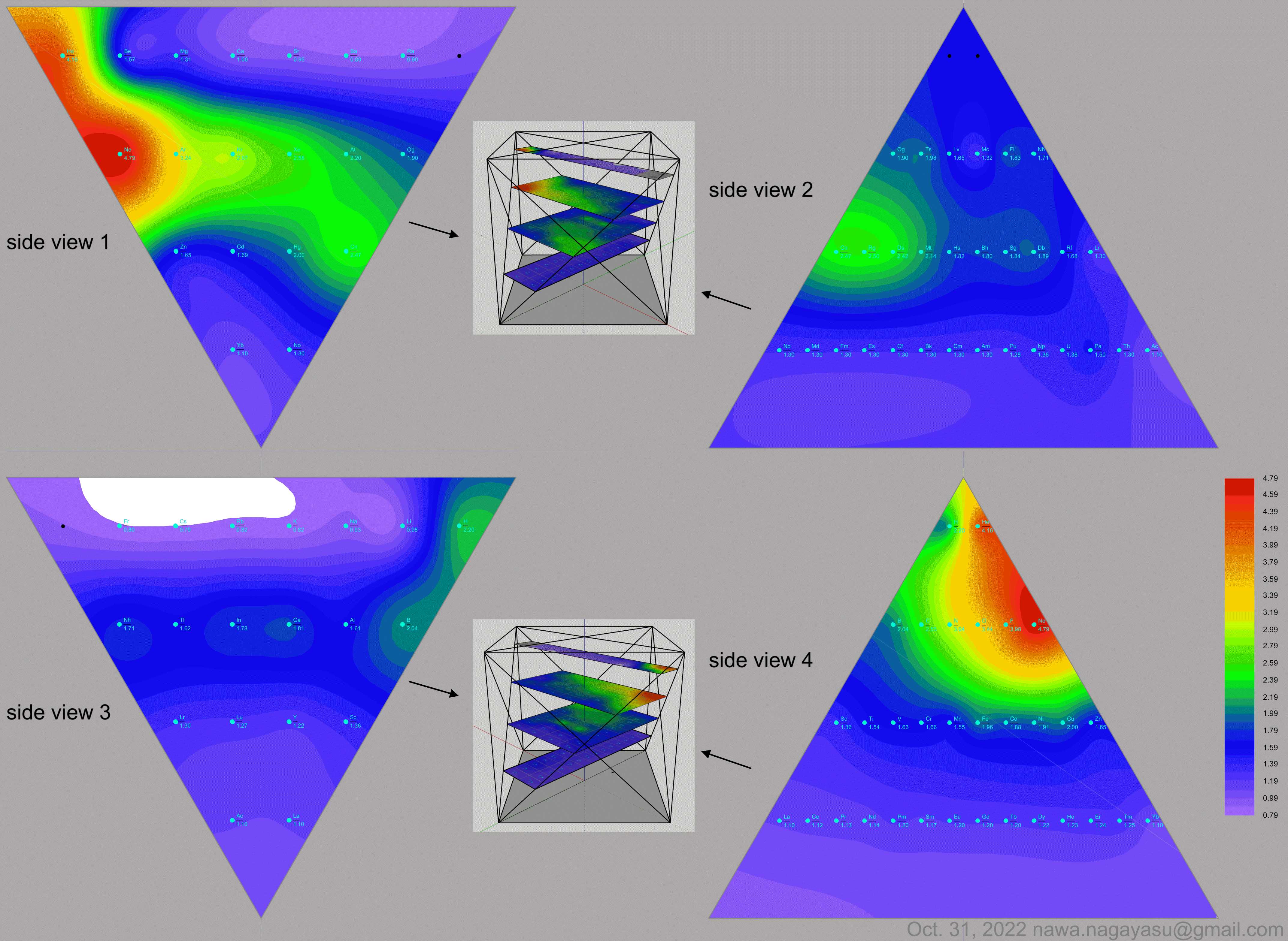
Nawa Nagayasu has mapped electronegativity to Mendeleeve's formulation:
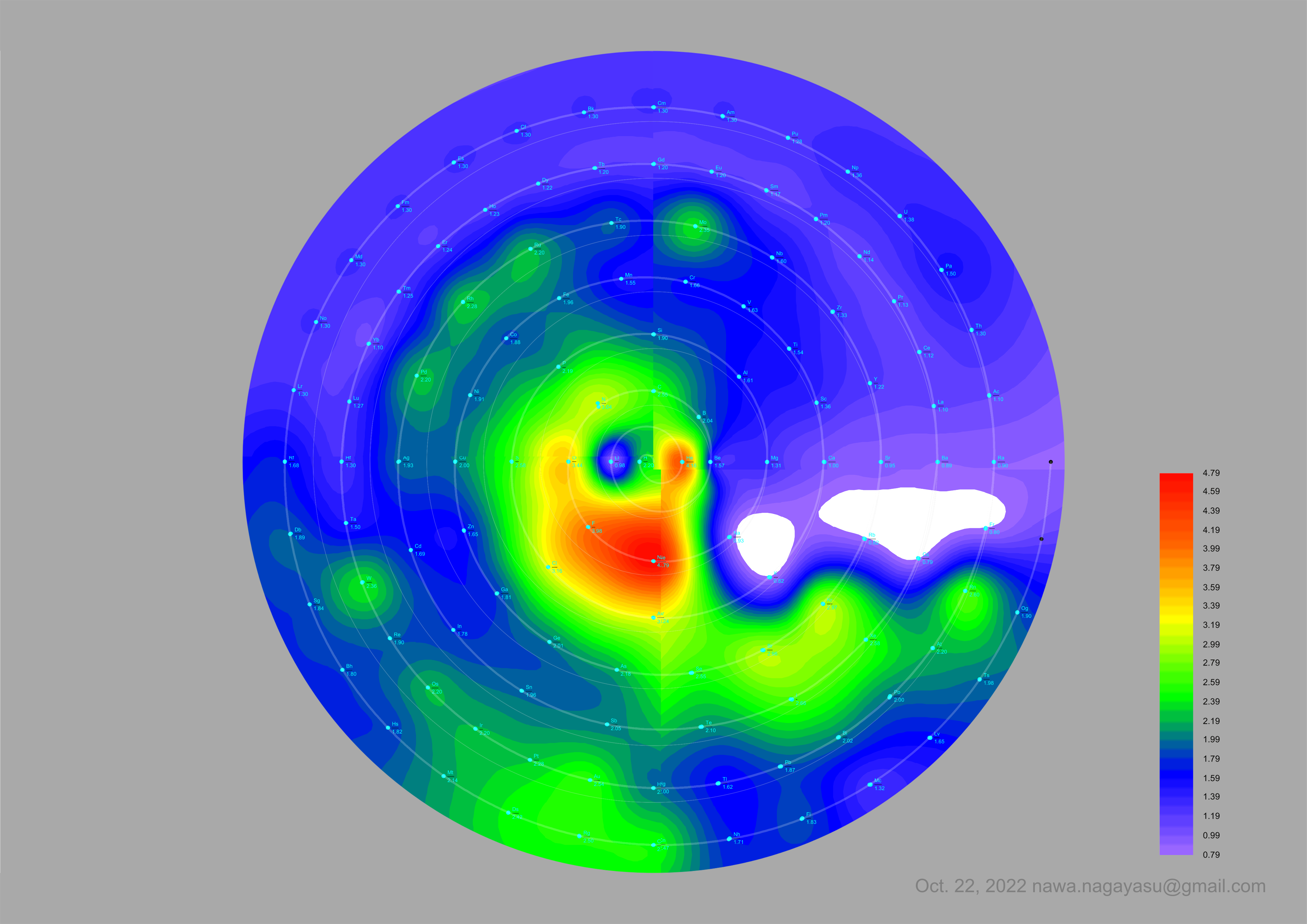
Nawa Nagayasu has mapped electronegativity onto other formulations, Julio's Binode Spiral:
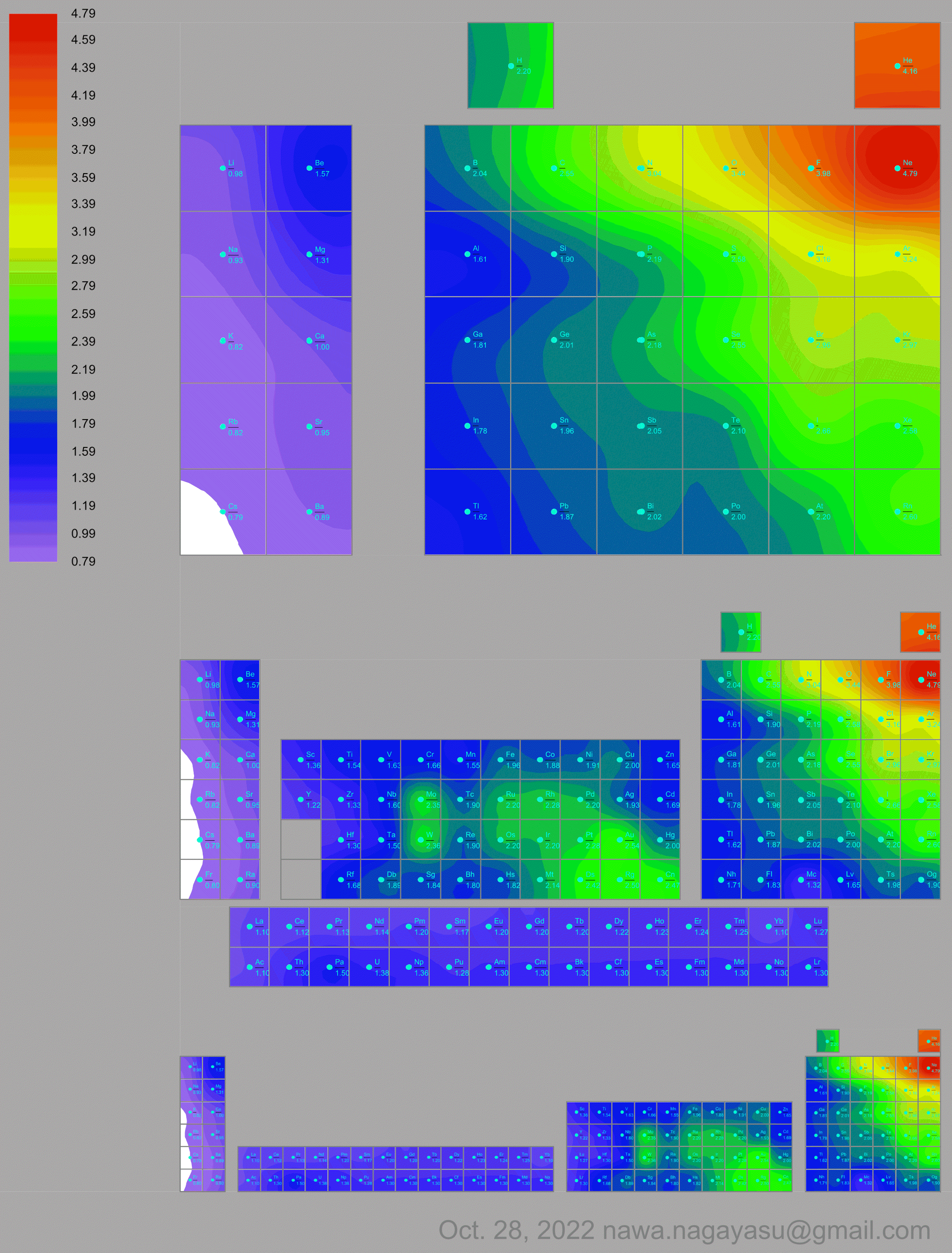
and the "conventional", short, medium and long forms of the periodic table with hydrogen above and between B & C which show the botom-right-to-top-left electronegativity trend:
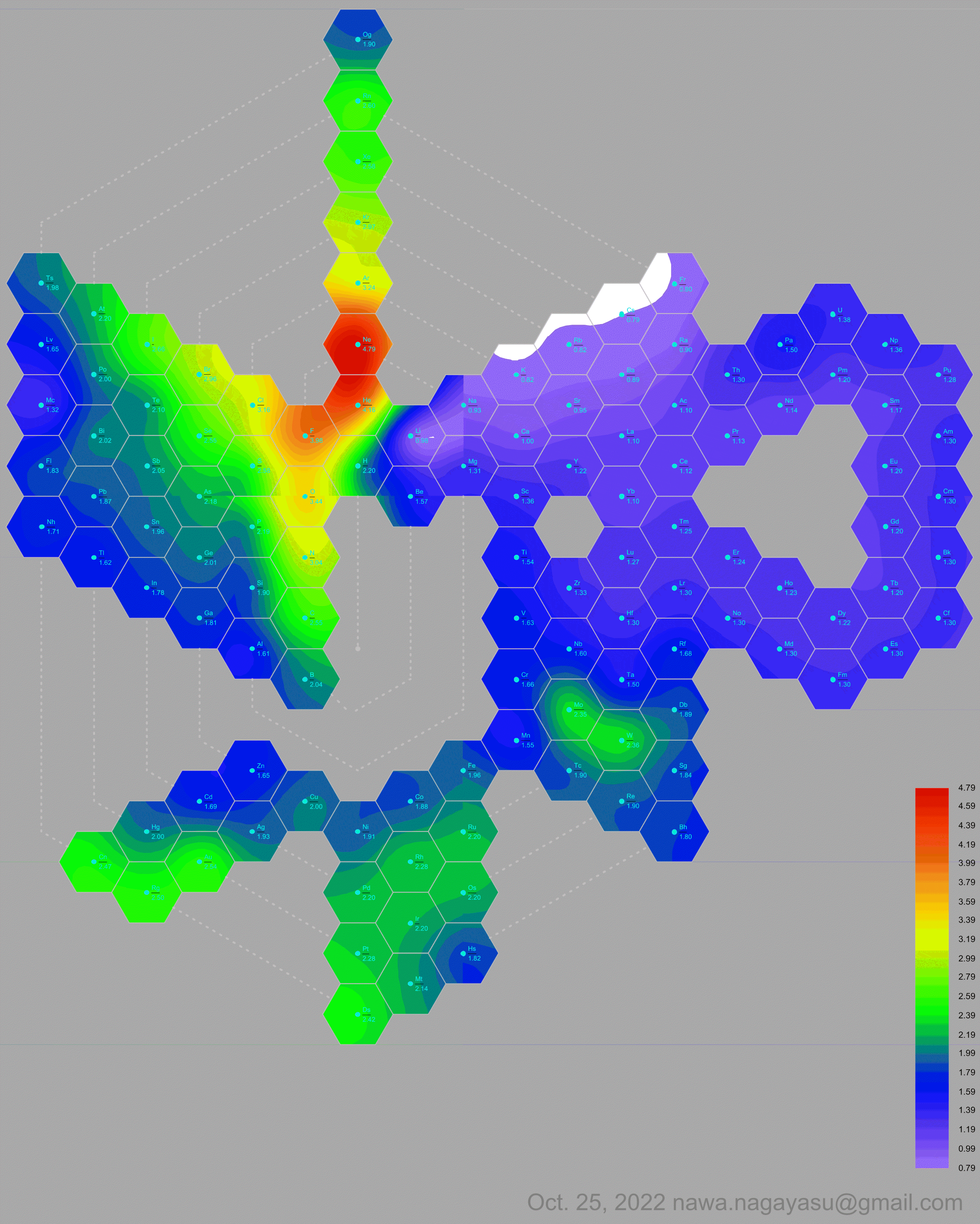
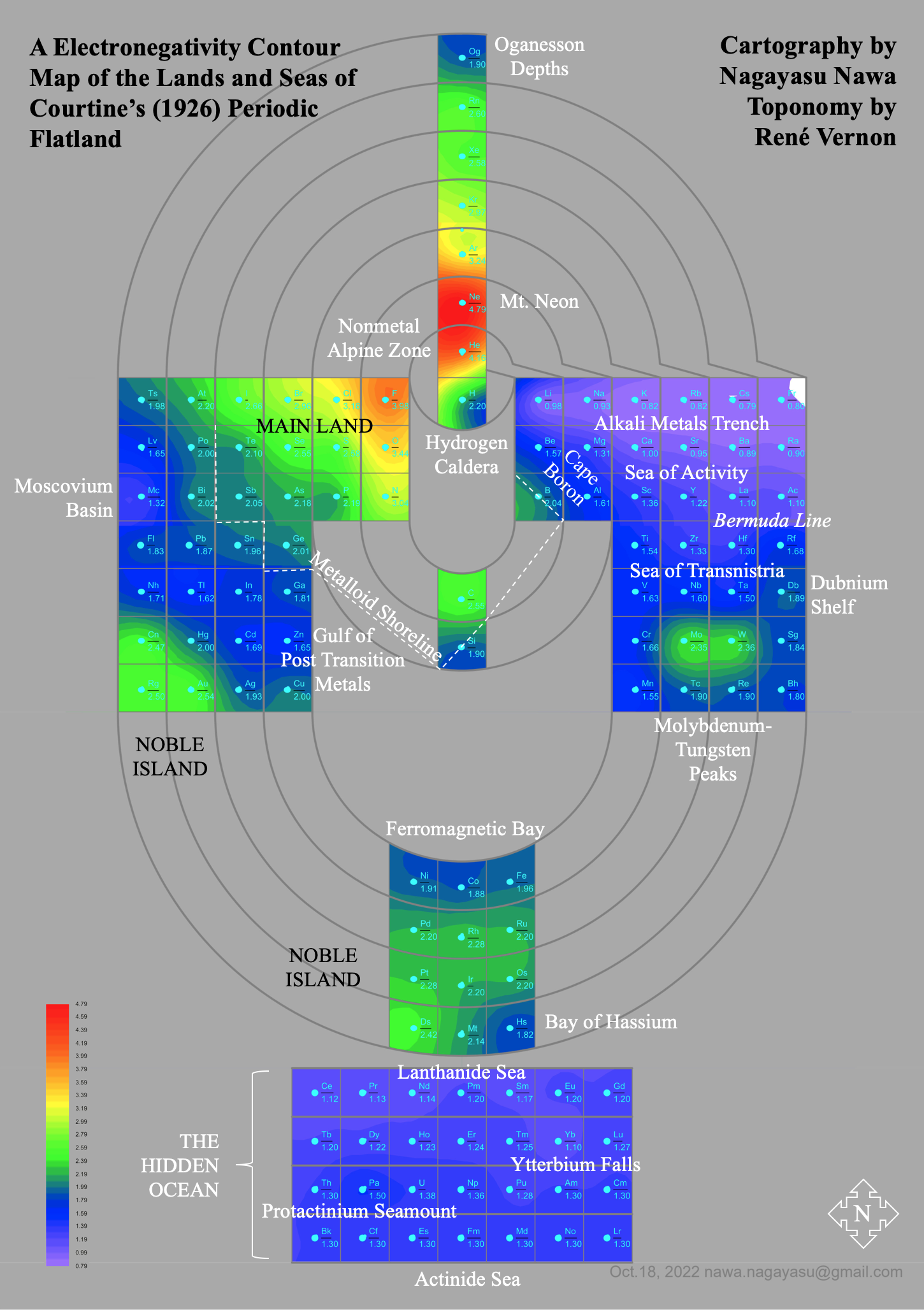
René Vernon's 777 Periodic Wedding Cake:
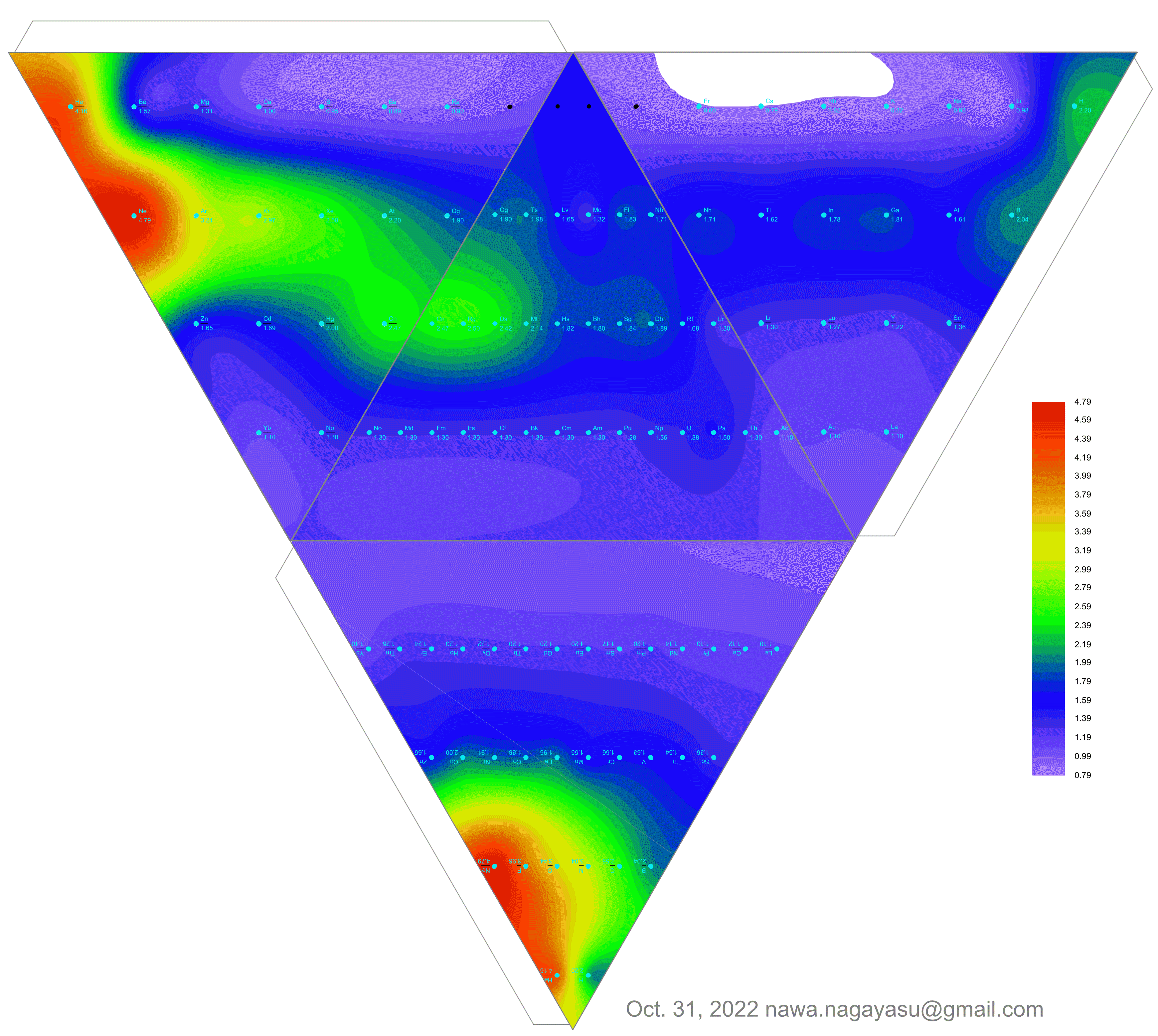
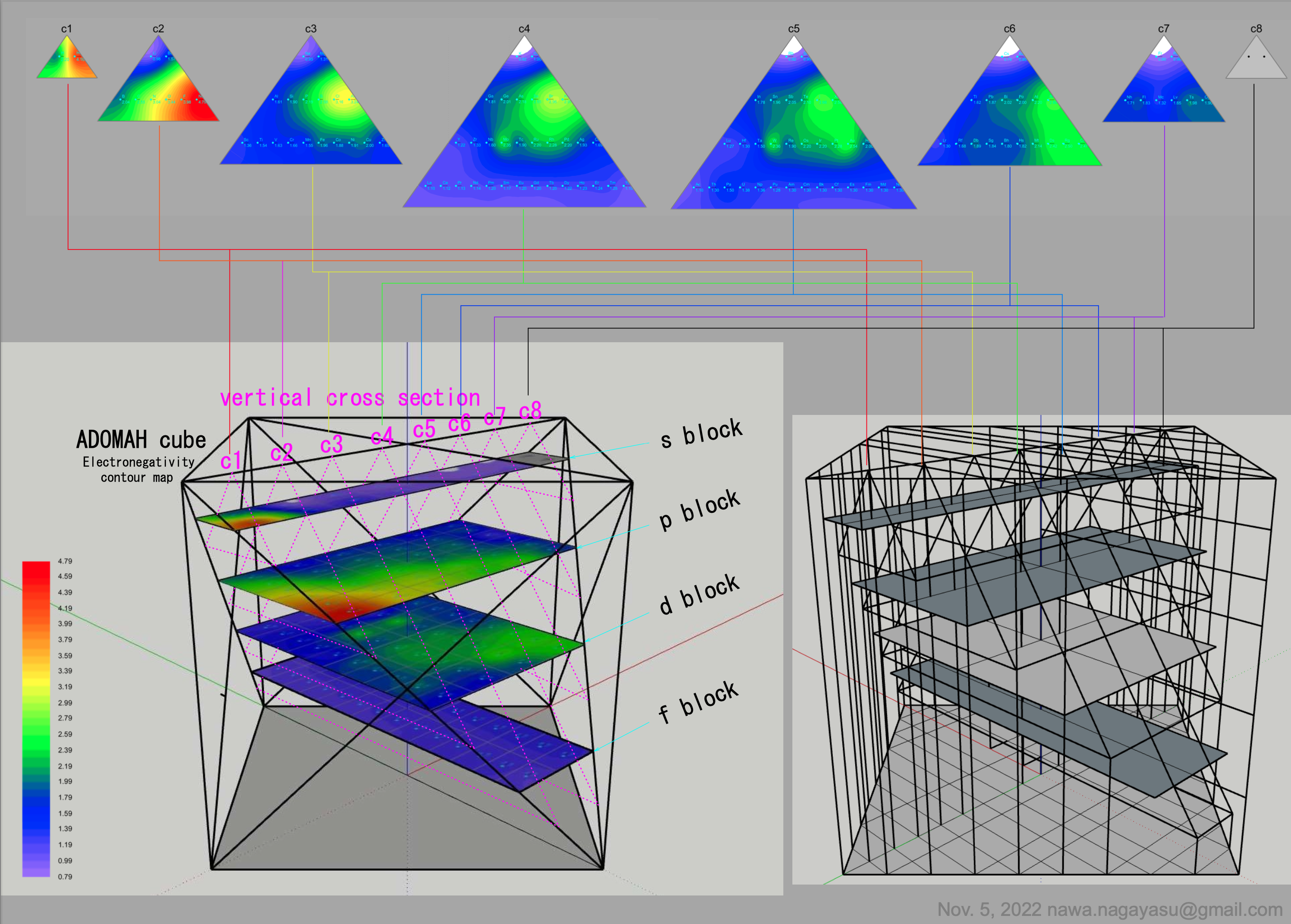
Valery Tsimmerman's ADOMAH formulation:
Valery Tsimmerman's ADOMAH tetrahedron (in a glass cube) formulation:
| Year: 2024 | PT id = 1303, Type = formulation |
Bilateral Symmetry in the Periodic Binodic Table
René Vernon, who developed these ideas, writes:
This table is adapted from the work of Gutiérrez-Samanez (2020), who discusses mathematising the chemical periodic system as a grid, which leads to a quadratic function or “binódica function” formed by pairs of periods or binodos (dyads).
The difference is that whereas Gutiérrez-Samanez showed the first pair of periods as H-He and Li-Be, this table shows the first period as e-n and H-He. Here, e is the electron and n is the neutron. Each pair of periods is shown pancake style rather than in a single row. The formula for the length of each paired period or binode is 2n2 = 2, 8, 16, 32.
The idea of paired periods has a long history; it seems to have originated with Werner in 1905.
According to Jensen:
"The temptation to read more into the shape of the table than is really there is almost overwhelming. Even someone as great as Werner was tempted (1905). Having postulated a missing element between H and He, he decided to perfect the symmetry of his table by guaranteeing that rows of differing length always occurred in pairs. Consequently, he further postulated a row of three missing elements lying above the H-X-He row."
Rydberg (1913, pp. 12–13) used a formula 4n^2 for the number of elements in the paired periods: 4, 16, 32, 64. This formula is also used by Gutiérrez-Samanez.
Paired periods were also used by Janet (1928), Saz (1931), Achimov (1946) and Baca Mendoza (1953).
References
- Achimov EI 1946, Zhur. Obshchei Khim., vol. 16, p. 961; https://www.meta-synthesis.com/webbook/35_pt/pt_database.php?PT_id=776
- Baca Mendoza O 1953, Leyes Genéticas de los elementos Químicos, Nuevo Sistema Periódico, National University of Cusco, https://www.meta-synthesis.com/webbook/35_pt/Mendoza_PT.pdf, accessed May 12, 2024
- Gutiérrez-Samanez JA 2020, Binódic periodic system: a mathematical approach, Found Chem, vol. 22, pp. 235–266 (255)
- Janet C1928, Essais de classification hélicoïdale des éléments chimiques. Imprimerie Départementale de l’Oise, Beauvais, https://www.meta-synthesis.com/webbook/35_pt/pt_database.php?PT_id=152
- Jensen WB 1986, Classification, symmetry and the periodic table, Computers & Mathematics with Applications, vol. 12B, no. 12, pp. 487–510 (508)
- Rydberg JR 1913, Untersuchungen über das system der grundstoffe, Lunds Univ. Ärsskrift, vol. 9, no. 18. In French: 1914, Recherches sur le système des éléments, Journal de Chimie Physique, vol. 12, p. 585
- Saz E 1931, Iberica, vol. 35, p. 186
- Wemer A 1905, Beitrag zum Aufbau des periodischen Systems, Ber. Deut. Chem. Ges, vol. 38, pp. 914–921, 2022–2027

 |
 |
 |
| What is the Periodic Table Showing? | Periodicity |
© Mark R. Leach Ph.D. 1999 –
Queries, Suggestions, Bugs, Errors, Typos...
If you have any:
Queries
Comments
Suggestions
Suggestions for links
Bug, typo or grammatical error reports about this page,please contact Mark R. Leach, the author, using mark@meta-synthesis.com
This free, open access web book is an ongoing project and your input is appreciated.