Periodic Table |
 |
 |
 |
 |
 |
 |
 |
| What is the Periodic Table Showing? | Periodicity |
The INTERNET Database of Periodic Tables
There are thousands of periodic tables in web space, but this is the only comprehensive database of periodic tables & periodic system formulations. If you know of an interesting periodic table that is missing, please contact the database curator: Mark R. Leach Ph.D. The database holds information on periodic tables, the discovery of the elements, the elucidation of atomic weights and the discovery of atomic structure (and much, much more).
The 10 most recent entries to the database:
| Year: 1925 | PT id = 1373, Type = structure |
Pauli and The Exclusion Principle
Pauli, W. Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren. Zeitschrift für Physik, 31, 765–783 (1925).
"Wolfgang Pauli was an Austrian–Swiss theoretical physicist and a pioneer of quantum mechanics. In 1945, after having been nominated by Albert Einstein, Pauli received the Nobel Prize in Physics 'for the discovery of the Exclusion Principle, also called the Pauli Principle'. The discovery involved spin theory.
"The Pauli exclusion principle (German: Pauli-Ausschlussprinzip) states that two or more identical particles with half-integer spins (i.e. fermions) cannot simultaneously occupy the same quantum state within a system that obeys the laws of quantum mechanics. This principle was formulated by Austrian physicist Wolfgang Pauli in 1925 for electrons, and later extended to all fermions with his spin–statistics theorem of 1940.
"In the case of electrons in atoms, the exclusion principle can be stated as follows: in a poly-electron atom it is impossible for any two electrons to have the same two values of all four of their quantum numbers, which are: n, the principal quantum number; ℓ, the azimuthal quantum number; mℓ, the magnetic quantum number; and ms, the spin quantum number.
"If two electrons reside in the same orbital, then their values of n, ℓ, and mℓ are equal. In that case, the two values of ms (spin) pair must be different. Since the only two possible values for the spin projection ms are +1/2 and –1/2, it follows that one electron must have ms = +1/2 and one ms = –1/2.
"To preserve the conservation of energy in beta decay, Pauli proposed the existence of a small neutral particle, dubbed the neutrino by Enrico Fermi, in 1930. Neutrinos were first detected in 1956. "
| Year: 1924 | PT id = 1372, Type = structure |
de Broglie and Wave–Particle Duality
de Broglie, L. Recherches sur la théorie des quanta. Annales de Physique, 3, 22–128 (1925). (Doctoral thesis, submitted 1924)
"Louis Victor Pierre Raymond, 7th Duc de Broglie was a French theoretical physicist and aristocrat known for his contributions to quantum theory. In his 1924 Ph.D. thesis, de Broglie postulated the wave nature of electrons and suggested that all matter has wave properties.
"This concept, now known as the de Broglie hypothesis, an example of wave–particle duality, and forms a central part of the theory of quantum mechanics. In 1929, de Broglie won the Nobel Prize in Physics, after the wave-like behaviour of matter was experimentally confirmed in 1927."

| Year: 1916 | PT id = 1371, Type = structure |
Sommerfeld and the Azimuthal and Magnetic Quantum Numbers
Sommerfeld, A. Zur Quantentheorie der Spektrallinien. Annalen der Physik, 51, 1–94 (1916).
"Arnold Sommerfeld was a German theoretical physicist who pioneered developments in both atomic and quantum physics. He also educated and mentored many students for the new era of theoretical quantum physics.
"Sommerfeld introduced the second (azimuthal) and the third (magnetic) quantum numbers ℓ and mℓ. (He also introduced the fine-structure constant and pioneered X-ray wave theory.)
"In quantum mechanics, the azimuthal quantum number ℓ is a quantum number for an atomic orbital that determines its orbital angular momentum and describes aspects of the angular shape of the orbital. The azimuthal quantum number is the second of a set of quantum numbers that describe the unique quantum state of an electron (the others being the principal quantum number n, the magnetic quantum number, mℓ, and the spin quantum number ms).
"Seven of Sommerfeld's doctoral students and postdoctoral supervisees: Werner Heisenberg, Wolfgang Pauli, Peter Debye, Hans Bethe, Linus Pauling, Isidor I. Rabi and Max von Laue went on to win Nobel Prizes in theoretical physics or chemistry. He also supervised at least 30 other famous physicists and chemists."

| Year: 1913 | PT id = 1370, Type = structure |
The Bohr Atom
Bohr, N. On the Constitution of Atoms and Molecules (Parts I–III). Philosophical Magazine, 26, 1–25; 476–502; 857–875 (1913).
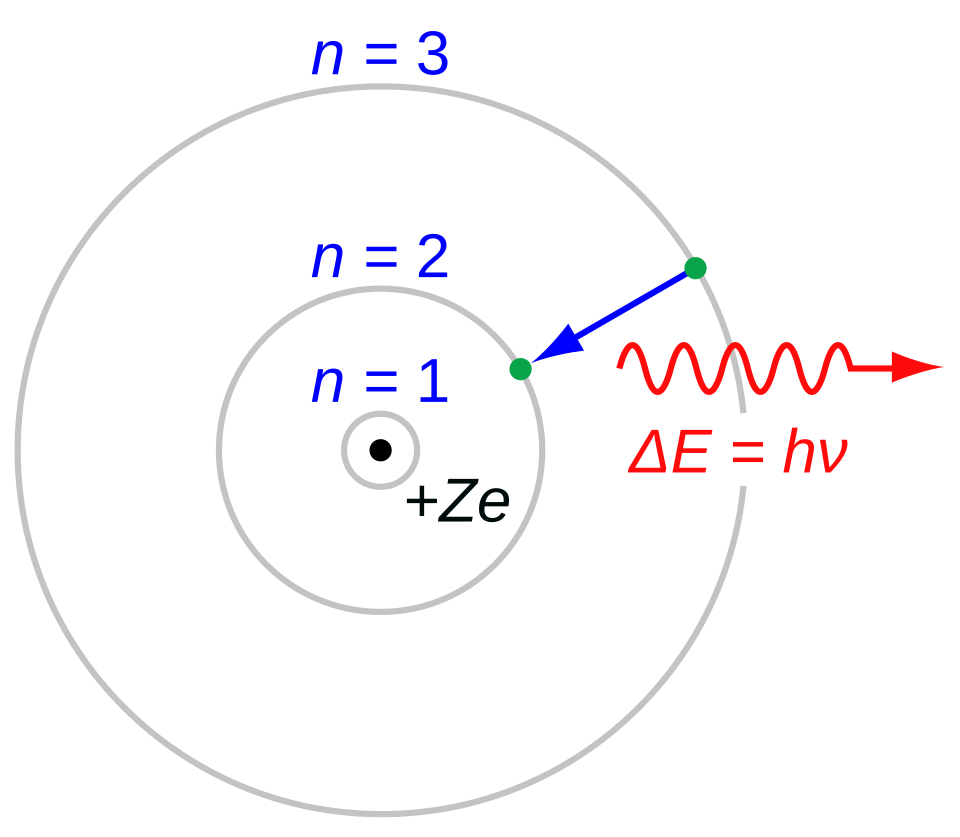
"In the Bohr model (or the Rutherford–Bohr model) of the hydrogen atom (Z = 1), the negatively charged electron confined to an atomic shell encircles a small, positively charged atomic nucleus. When an electron jumps between orbits, is accompanied by an emitted or absorbed amount of electromagnetic energy (where E = hν). The orbits in which the electron may travel are shown as grey circles; their radius increases as n2, where n is the principal quantum number. The 3 ? 2 transition produces the first line of the Balmer series, and for hydrogen (Z = 1) it results in a photon of wavelength 656 nm (red light).
"The Bohr atom consists of a small, dense atomic nucleus surrounded by orbiting electrons. It is analogous to the structure of the Solar System, but with attraction provided by electrostatic force rather than gravity, and with the electron energies quantised (assuming only discrete values). The Bohr model incorporated some early quantum concepts. Developed from 1911 to 1918 by Niels Bohr and building on Ernest Rutherford's discovery of the atom's nucleus, the model supplanted the plum pudding model of J. J. Thomson only to be replaced by the quantum atomic model in the 1920s.
"The Bohr model's key success lies in explaining the Rydberg formula for hydrogen's spectral emission lines. While the Rydberg formula had been known experimentally, it did not gain a theoretical basis until the Bohr model was introduced. Not only did the Bohr model explain the reasons for the structure of the Rydberg formula, it also provided a justification for the fundamental physical constants that make up the formula's empirical results."
| Year: 1911 | PT id = 1369, Type = structure |
Rutherford and the Geiger–Marsden Gold Leaf Scattering Experiments
Geiger, H., & Marsden, E. On a Diffuse Reflection of the ?-Particles. Proceedings of the Royal Society A, 82, 495–500 (1909) and Rutherford, E. The Scattering of ? and ? Particles by Matter and the Structure of the Atom. Philosophical Magazine, 21, 669–688 (1911).
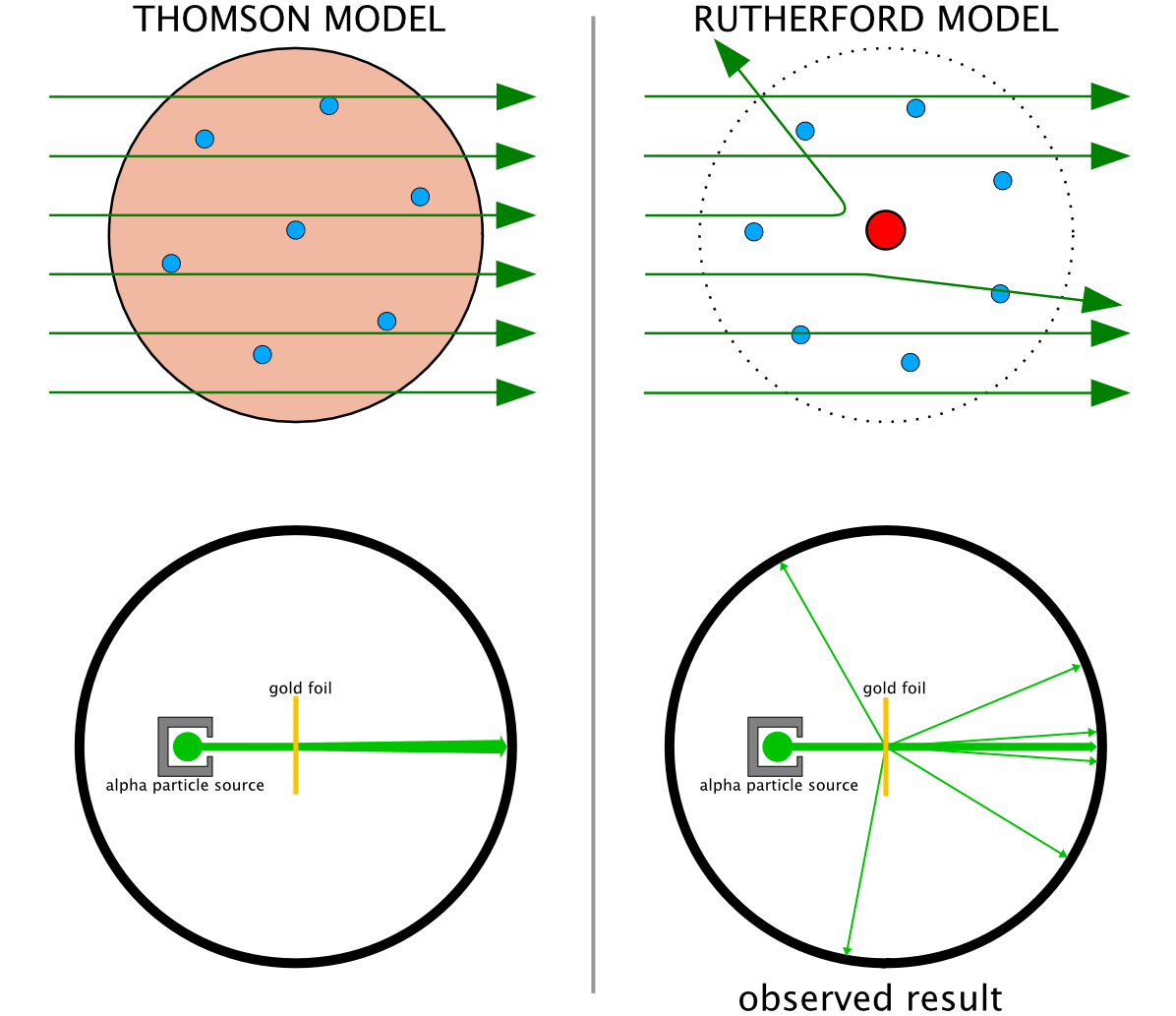
"The Rutherford scattering experiments were performed between 1906 and 1913 by Hans Geiger and Ernest Marsden under the direction of Ernest Rutherford at the Physical Laboratories of the University of Manchester.
"Experiments showed that every atom had a nucleus where all its positive charge and most of its mass is concentrated. This was deduced this after measuring how a beam of alpha particles is scattered when it strikes gold leaf (thin gold foil)."
| Year: 1904 | PT id = 1368, Type = structure |
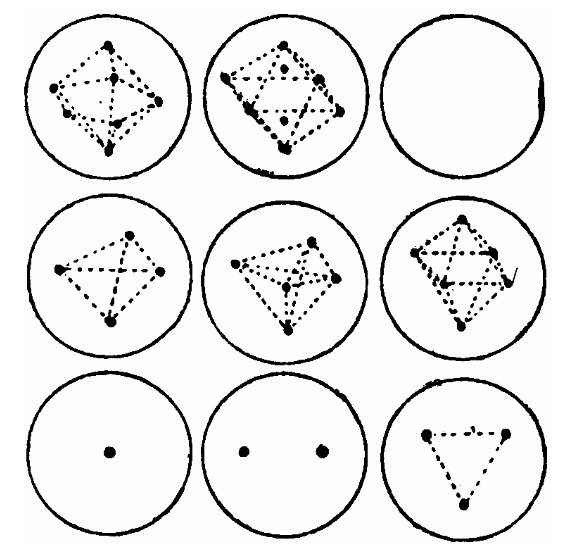
Thomson and the Plum Pudding Model of the Atom
Thomson, J. J. On the Structure of the Atom. Philosophical Magazine, 7, 237–265 (1904). https://zenodo.org/records/1430726
"The view that the atoms of the elements consist of a number of negatively electrified corpuscles enclosed in a sphere of uniform positive electrification, suggests, among other interesting mathematical problems, the one discussed in this paper, that of the motion of a ring of n negatively electrified particles placed inside a uniformly electrified sphere."

| Year: 1900 | PT id = 1367, Type = structure |
Planck and E = hν
Planck, M. Über das Gesetz der Energieverteilung im Normalspektrum (On the law of energy distribution in the normal spectrum). Annalen der Physik, 4, 553–563 (1901). (Presented to the German Physical Society in Dec 1900).
"In 1894, Planck turned his attention to the problem of black-body radiation which had been stated by Kirchhoff in 1859 as: 'How does the intensity of the electromagnetic radiation emitted by a black body (a perfect absorber, also known as a cavity radiator) depend on the frequency of the radiation (i.e., the colour of the light) and the temperature of the body?'
The central assumption of Planck’s new analysis, the Planck postulate, was that electromagnetic energy could be emitted only in quantized form; in other words, the energy could only be a multiple of an elementary unit:
E = hν
Where h is the Planck constant, also known as Planck's action quantum and ν (the Greek letter 'nu') is the frequency of the radiation."

| Year: 2025 | PT id = 1366, Type = formulation review |
The Surprisingly Beautiful Origins of the Periodic Table
A video about The Surprisingly Beautiful Origins of the Periodic Table by Chemistorian.
"The periodic table is probably the most iconic image in science. Join me to hear the story about its origins, from ancient philosophers speculating about the nature of matter to the earliest chemists who tried to find the mysterious connection between the elements. Learn about Döbereiner's chemical traids, De Chancourtois' Telluric Screw, Mendeleev's amazing predictions, and much more!"
Thanks to Eric Scerri for the tip!
| Year: 2026 | PT id = 1365, Type = formulation |
Pairs and Squares Periodic Table
"Pairs and Squares" Periodic Table by Leonid A. Levin of Boston University
Leonid writes:
"All the tables [in the PT Database] share a common problem: their irregularity exceeds by far their periodicity.
"In my youth I was greatly bothered by this. Yet, taking advantage of a few patterns in atomic orbitals allows a complete elimination of all irregularities, putting all periods in a perfect pattern.This perfectly regular rendition would be much more comfortable, especially at one's first high school exposure to this Science symbol.I am attaching such "Pairs and Squares" rendition with a brief explanation."
"Read more in the full 'Pairs and Squares' paper, here."

| Year: 2007 | PT id = 1364, Type = formulation |
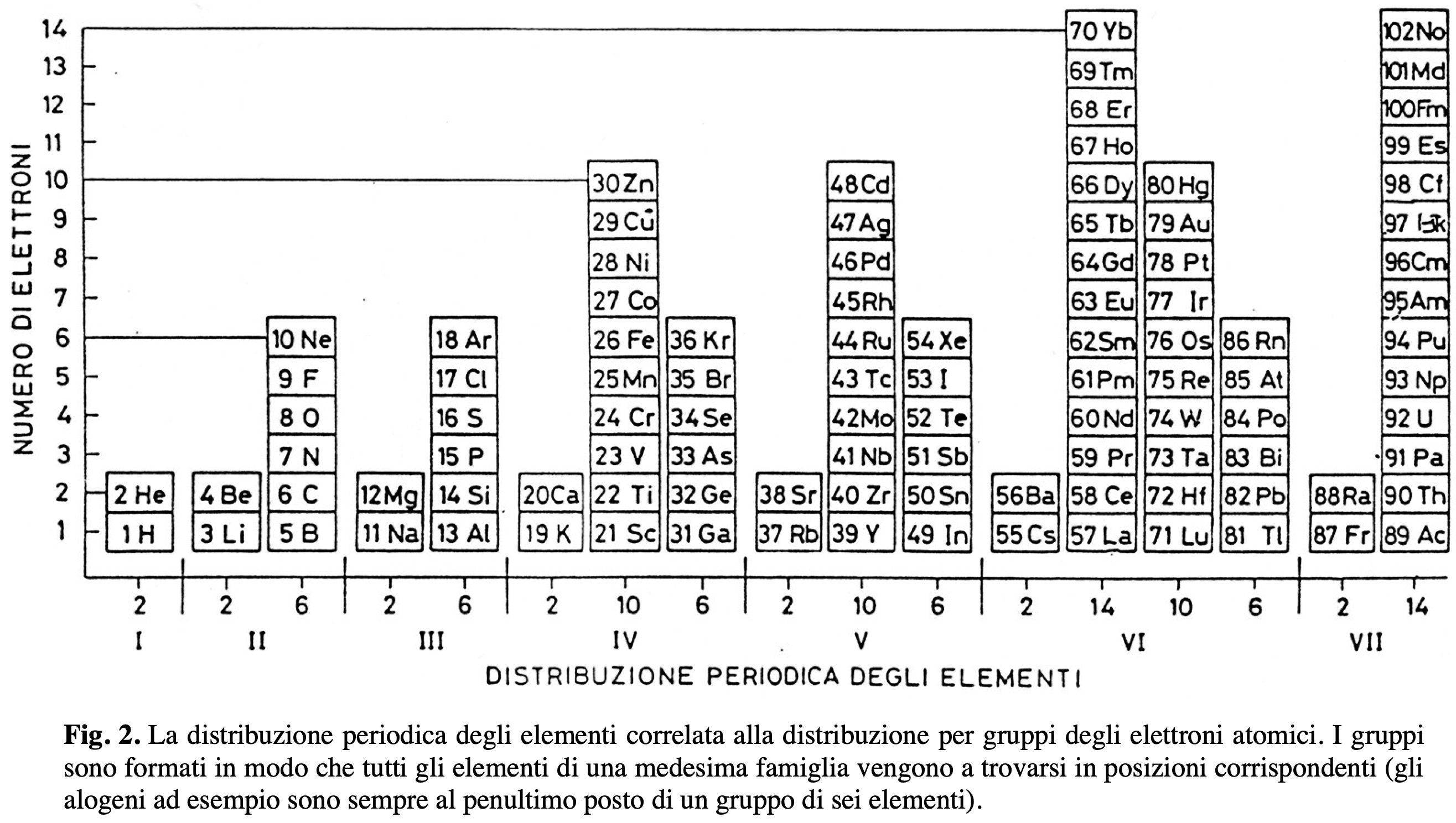
Distribuzione Peridica Degli Elemnti
Distribuzione Peridica Degli Elemnti – Periodic Distribution of Elements – by Leonello Paoloni.
From La Chimica nella Scuola, Sept. 2007, pp 111.
"Fig. 2. The periodic distribution of elements correlates with the group distribution of atomic electrons. Groups are formed so that all elements of the same family are found in corresponding positions (for example, the halogens are always in the second-to-last position in a group of six elements)." (Google Translate)
Thanks to Eric Scerri for the tip!
 |
 |
 |
| What is the Periodic Table Showing? | Periodicity |
© Mark R. Leach Ph.D. 1999 –
Queries, Suggestions, Bugs, Errors, Typos...
If you have any:
Queries
Comments
Suggestions
Suggestions for links
Bug, typo or grammatical error reports about this page,please contact Mark R. Leach, the author, using mark@meta-synthesis.com
This free, open access web book is an ongoing project and your input is appreciated.